_Задания для подготовки к огэ квадратные уравнения уравнения_. Решение(по дискриминанту). D(1) 2 1 2 1 2 Ответ 23. Задание 1

• Название: Решение(по дискриминанту). D(1) 2 1 2 1 2 Ответ 23. Задание 1
• Дата: 13.10.2022
• Размер: 0.55 Mb.
• Имя файла: _Задания для подготовки к огэ квадратные уравнения уравнения_.docx
• Тип: Решение; #731075

Задание 1

Решите урав­не­ние  .

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

Решение(по дискриминанту).









D=(-1)²

_{1=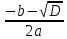 2=
1= 2=}
Ответ: −23.

1. Задание 1

Найдите корни урав­не­ния 

Если кор­ней несколько, за­пи­ши­те их в ответ без пробелов в порядке возрастания.

2. Задание 1

Решите урав­не­ние 8x² − 12x + 4 = 0.

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

3. Задание 1

Най­ди­те корни урав­не­ния 

Если кор­ней несколько, за­пи­ши­те их в ответ без пробелов в порядке возрастания.

4. Задание 1

Решите уравнение   Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

5. Задание 1

Решите уравнение   Если уравнение имеет более одного корня, в ответ запишите больший из корней.

6. Задание 1

Решите уравнение   Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

7. Задание 1

Решите уравнение   Если уравнение имеет более одного корня, в ответ запишите больший из корней.

8. Задание 1

Решите уравнение   Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

9. Задание 1

Решите уравнение   Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

10. Задание 1

Решите уравнение   Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

11. Задание 1

Решите уравнение   Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

Задание 2

Решите урав­не­ние  .

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

Решение.

Запишем урав­не­ние в виде 

Далее решаем по дискриминанту.

1. Задание 2

Най­ди­те корни урав­не­ния 

Если кор­ней несколько, за­пи­ши­те их в ответ без пробелов в порядке возрастания.

2. Задание 2

Най­ди­те корни урав­не­ния 

Если кор­ней несколько, за­пи­ши­те их в ответ без пробелов в порядке возрастания.

3. Задание 2

Най­ди­те корни урав­не­ния 

Если кор­ней несколько, за­пи­ши­те их в ответ без пробелов в порядке возрастания.

4. Задание 2

Най­ди­те корни урав­не­ния 

Если кор­ней несколько, за­пи­ши­те их в ответ без пробелов в порядке возрастания.

5. Задание 2

Най­ди­те корни урав­не­ния 

Если кор­ней несколько, за­пи­ши­те их в ответ без пробелов в порядке возрастания.

6. Задание 2

Най­ди­те корни урав­не­ния 

Если кор­ней несколько, за­пи­ши­те их в ответ без пробелов в порядке возрастания.

7. Задание 2

Най­ди­те корни урав­не­ния 

Если кор­ней несколько, за­пи­ши­те их в ответ без пробелов в порядке возрастания.

8. Задание 2

Решите уравнение 

Если уравнение имеет более одного корня, в ответ запишите больший из корней.

9. Задание 2 

Решите уравнение  .

10. Задание 2 

Решите уравнение  .

Задание 3

Решите урав­не­ние  .

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

Решение.

Запишем урав­не­ние в виде    Далее решаем по дискриминанту.

 

Ответ: −24.
1. Задание 3

Решите уравнение  .

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

2. Задание 3

Решите урав­не­ние   .

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

3. Задание 3

Решите уравнение  .

4. Задание 3

Решите уравнение  .

5. Задание 3

Решите уравнение  .

6. Задание 3

Решите уравнение  .

7. Задание 3

Решите уравнение  .

8. Задание 3

Решите уравнение  .

9. Задание 3

Решите уравнение  .

10. Задание 3

Решите уравнение  .

Задание 4

Найдите корни урав­не­ния   .

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

Решение.

Решим уравнение:

 



Ответ: −0,20,2.

1. Задание 4

Найдите корни урав­не­ния   .

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

2. Задание 4

Решите урав­не­ние 

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

3. Задание 4

Решите уравнение   Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

4. Задание 4

Решите уравнение   Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

5. Задание 4

Решите уравнение   Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

6. Задание 4

Решите уравнение   Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

7. Задание 4

Решите уравнение   Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

8. Задание 4

Решите уравнение   Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

9. Задание 4

Решите уравнение   Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

10. Задание 4

Решите уравнение   Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

Задание 5

Найдите корни урав­не­ния   .

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

Решение.

Последовательно получаем:

 



Ответ: 05.

1. Задание 5

Найдите корни урав­не­ния   .

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

2. Задание 5

Решите урав­не­ние   .

Если кор­ней несколько, за­пи­ши­те их в ответ без пробелов в порядке возрастания.

3. Задание 5

Най­ди­те корни урав­не­ния 

Если кор­ней несколько, за­пи­ши­те их в ответ без пробелов в порядке возрастания.

4. Задание 5

Най­ди­те корни урав­не­ния 

Если кор­ней несколько, за­пи­ши­те их в ответ без пробелов в порядке возрастания.

5. Задание 5

Най­ди­те корни урав­не­ния 

Если кор­ней несколько, за­пи­ши­те их в ответ без пробелов в порядке возрастания.

6. Задание 5

Най­ди­те корни урав­не­ния



Если кор­ней несколько, за­пи­ши­те их в ответ без пробелов в порядке возрастания.

7. Задание 5

Най­ди­те корни урав­не­ния 

Если кор­ней несколько, за­пи­ши­те их в ответ без пробелов в порядке возрастания.

8. Задание 5

Най­ди­те корни урав­не­ния 

Если кор­ней несколько, за­пи­ши­те их в ответ без пробелов в порядке возрастания.

9. Задание 5

Най­ди­те корни урав­не­ния 

Если кор­ней несколько, за­пи­ши­те их в ответ без пробелов в порядке возрастания.

10. Задание 5

Най­ди­те корни урав­не­ния 

Если кор­ней несколько, за­пи­ши­те их в ответ без пробелов в порядке возрастания.

Задание 6 

Най­ди­те корни урав­не­ния 

Если кор­ней несколько, за­пи­ши­те их в ответ без пробелов в порядке возрастания.

Решение.

Запишем урав­не­ние в виде:

 



 

 Далее решаем по дискриминанту.
Ответ: 14.

1. Задание 6 

Най­ди­те корни урав­не­ния 

Если кор­ней несколько, за­пи­ши­те их в ответ без пробелов в порядке возрастания.

2. Задание 6 

Най­ди­те корни урав­не­ния 

Если кор­ней несколько, за­пи­ши­те их в ответ без пробелов в порядке возрастания

3. Задание 6

Най­ди­те корни урав­не­ния 

Если кор­ней несколько, за­пи­ши­те их в ответ без пробелов в порядке возрастания.

4. Задание 6 

Найдите корни урав­не­ния 

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

5. Задание 6 

Найдите корни уравнения x²​ + 3x = 10.

Если кор­ней несколько, за­пи­ши­те их в ответ без пробелов в порядке возрастания.

6. Задание 6 

Найдите корни урав­не­ния 

7. Задание 6 

Найдите корни урав­не­ния 

8. Задание 6 

Решите уравнение   Если уравнение имеет более одного корня, в ответ запишите больший из корней.

9. Задание 6 

Решите уравнение   Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

Задание 7

Две пря­мые пе­ре­се­ка­ют­ся в точке C (см. рис.). Най­ди­те абс­цис­су точки C.

Решение.

Уравнения прямых:

 



 

Найдём абс­цис­су точки пе­ре­се­че­ния прямых, для этого, при­рав­ня­ем ординаты:

 



 

Ответ: −2.

1. Задание 7



Две пря­мые пересекаются в точке C (см. рис.). Най­ди­те абсциссу точки  C.

2. Задание 7



Две прямые пересекаются в точке C (см. рис.). Найдите абсциссу точки  C.
3. Задание 7



Две прямые пересекаются в точке C (см. рис.). Найдите абсциссу точки  C.

4. Задание 7



Две прямые пересекаются в точке C (см. рис.). Найдите абсциссу точки  C.

5. Задание 7



Две прямые пересекаются в точке C (см. рис.). Найдите абсциссу точки  C.

Задание 8

На ри­сун­ке изоб­ра­же­ны гра­фи­ки функ­ций   и   Вы­чис­ли­те ко­ор­ди­на­ты точки B.

Запишите ко­ор­ди­на­ты в от­ве­т без пробелов и знаков препинания.
Решение.

Точки A и B — точки пе­ре­се­че­ния гра­фи­ков функ­ций   и   Найдём их абсциссы:

 



 

Абсцисса точки B боль­ше нуля, следовательно, это   Найдём ор­ди­на­ту точки B: 

 

Ответ: 3−6.

1. Задание 8

На ри­сун­ке изоб­ра­же­ны гра­фи­ки функ­ций y = 6 − x² и y = − x. Вы­чис­ли­те абс­цис­су точки B.

2. Задание 8

На ри­сун­ке изоб­ра­же­ны гра­фи­ки функ­ций y = 5 − x² и y = 4x. Вы­чис­ли­те абс­цис­су точки B.

3. Задание 8

На рисунке изображены графики функций   и  . Вычислите абсциссу точки  .



4. Задание 8

На рисунке изображены графики функций   и  . Вычислите абсциссу точки B.



5. Задание 8



На рисунке изображены графики функций y=3− x 2 и y=2x . Вычислите координаты точки B .

6. Задание 8



На рисунке изображены графики функций y=2− x 2 и y=−x . Вычислите координаты точки B .

7. Задание 8



На рисунке изображены графики функций y=2− x 2 и y=x . Вычислите координаты точки B .

8. Задание 8

На рисунке изображены графики функций y = 6 − x² и y = 5x. Вычислите абсциссу точки B.

Задание 9

Квадратный трёхчлен раз­ло­жен на множители:   Най­ди­те 

Решение.

Корни урав­не­ния    находим по дискриминанту. Это числа −9 и 3. По формуле   где   и   корни уравнения  получаем   Следовательно, 

1. Задание 9

Квадратный трёхчлен раз­ло­жен на множители:   Най­ди­те 

2. Задание 9

Квадратный трёхчлен разложен на множители:   Найдите a.

Задание 10

Решите урав­не­ние 

Решение.

Последовательно получаем:









Ответ: −9,7.

1. Задание 10

Решите урав­не­ние 

2. Задание 10

Решите урав­не­ние 

3. Задание 10

Решите урав­не­ние 

4. Задание 10

Решите урав­не­ние 

5. Задание 10

Решите урав­не­ние 

6. Задание 10

Решите урав­не­ние 

7. Задание 10

Решите урав­не­ние 

8. Задание 10

Решите урав­не­ние 

9. Задание 10

Решите урав­не­ние 

10. Задание 10

Решите урав­не­ние 

Задание 11

Решите урав­не­ние 

Решение.

Раскроем скоб­ки и пре­об­ра­зу­ем выражение:

 





Ответ: 2,25.

1. Задание 11 

Решите урав­не­ние 

2. Задание 11

Решите урав­не­ние 10x² − 17x + 34 = 7x² − 26x + 28.

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

3. Задание 11

Решите урав­не­ние 

4. Задание 11

Решите урав­не­ние 

5. Задание 11

Решите урав­не­ние 

6. Задание 11

Решите урав­не­ние 

7. Задание 11

Решите урав­не­ние 

8. Задание 11

Решите урав­не­ние 

9. Задание 11

Решите урав­не­ние 

10. Задание 11

Решите урав­не­ние 

Задание 12

Решите урав­не­ние 

Решение.

Квадраты чисел равны, если числа равны или противоположны:

 



 

Ответ: −2,5.

 

Приведем дру­гое решение.

Раскроем скоб­ки в обеих ча­стях уравнения:

 



 

Приведем дру­гое решение.

Воспользуемся фор­му­лой разности квадратов:

 



1. Задание 12

Решите урав­не­ние (x − 9)² = (x − 3)².

2. Задание 12

Решите уравнение 

3. Задание 12

Решите урав­не­ние 

4. Задание 12

Решите урав­не­ние 

5. Задание 12

Решите урав­не­ние 

6. Задание 12

Решите урав­не­ние 

7. Задание 12

Решите урав­не­ние 

8. Задание 12

Решите урав­не­ние 

9. Задание 12

Решите урав­не­ние 

10. Задание 12

Решите урав­не­ние 

Задание 13

Уравнение   имеет корни −5; 7. Най­ди­те 

Решение.

По тео­ре­ме Виета 

 

Ответ: −35.

1. Задание 13

Уравнение   имеет корни −5; 2. Найдите 

2. Задание 13

Уравнение   имеет корни −9; 1. Найдите 

3. Задание 13

Уравнение   имеет корни 5; 9. Найдите 

4. Задание 13

Уравнение   имеет корни −6; 1. Найдите 

5. Задание 13

Уравнение   имеет корни −4; −1. Найдите 

6. Задание 13

Уравнение   имеет корни −2; 1. Найдите 

7. Задание 13

Уравнение   имеет корни −9; 6. Найдите 

8. Задание 13

Уравнение   имеет корни −2; 7. Найдите 

9. Задание 13

Уравнение   имеет корни 1; 6. Найдите 

10. Задание 13

Уравнение   имеет корни −3; 3. Найдите