Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы
 Скачать 11.59 Kb. Скачать 11.59 Kb.
|
|
Симплекс-метод. Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы. Определим минимальное значение целевой функции F(X) = 90x1+180x2+200x3 при следующих условиях-ограничений. 14x1+16x2+28x3≤362 28x1+41x2+14x3≤276 42x1+56x2+28x3≤310 Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме). В 1-м неравенстве смысла (≤) вводим базисную переменную x4. В 2-м неравенстве смысла (≤) вводим базисную переменную x5. В 3-м неравенстве смысла (≤) вводим базисную переменную x6. 14x1+16x2+28x3+x4 = 362 28x1+41x2+14x3+x5 = 276 42x1+56x2+28x3+x6 = 310 Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид: 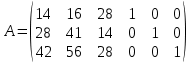 Базисные переменные это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом. Решим систему уравнений относительно базисных переменных: x4, x5, x6 Полагая, что свободные переменные равны 0, получим первый опорный план: X0 = (0,0,0,362,276,310) Базисное решение называется допустимым, если оно неотрицательно.
Переходим к основному алгоритму симплекс-метода. 1. Проверка критерия оптимальности. Среди значений индексной строки нет положительных. Поэтому эта таблица определяет оптимальный план задачи. Окончательный вариант симплекс-таблицы:
Оптимальный план можно записать так: x1 = 0, x2 = 0, x3 = 0 F(X) = 90∙0 + 180∙0 + 200∙0 = 0 Анализ оптимального плана. В оптимальный план вошла дополнительная переменная x4. Следовательно, при реализации такого плана имеются недоиспользованные ресурсы 1-го вида в количестве 362. В оптимальный план вошла дополнительная переменная x5. Следовательно, при реализации такого плана имеются недоиспользованные ресурсы 2-го вида в количестве 276. В оптимальный план вошла дополнительная переменная x6. Следовательно, при реализации такого плана имеются недоиспользованные ресурсы 3-го вида в количестве 310. Значение 0 в столбце x4 означает, что теневая цена (двойственная оценка) равна y1=0. Значение 0 в столбце x5 означает, что теневая цена (двойственная оценка) равна y2=0. Значение 0 в столбце x6 означает, что теневая цена (двойственная оценка) равна y3=0. Примечание: 1. По какому методу пересчитываются симплекс-таблицы? Используется правило прямоугольника (метод жордановских преобразований). 2. Обязательно ли каждый раз выбирать максимальное значение из индексной строки? Можно не выбирать, но это может привести к зацикливанию алгоритма. 3. В индексной строке в n-ом столбце нулевое значение. Что это означает? Нулевые значения должны соответствовать переменным, вошедшим в базис. Если в индексной строке симплексной таблицы оптимального плана находится нуль, принадлежащий свободной переменной, не вошедшей в базис, а в столбце, содержащем этот нуль, имеется хотя бы один положительный элемент, то задача имеет множество оптимальных планов. Свободную переменную, соответствующую указанному столбцу, можно внести в базис, выполнив соответствующие этапы алгоритма. В результате будет получен второй оптимальный план с другим набором базисных переменных. Решение было получено и оформлено с помощью сервиса: Решение симплекс-методом Вместе с этой задачей решают также: Графический метод решения задач линейного программирования Двойственный симплекс-метод Двойственная задача линейного программирования Метод Гомори Транспортная задача Расчет сетевого графика |
