Расчет геометрических параметров и ДН антенны. Рис. Конструкция вибраторного облучателя 1
 Скачать 355.97 Kb. Скачать 355.97 Kb.
|
|
Конструкция облучателя приведена на рис. 1 [1]. Для определения конструктивных размеров облучателя рассчитаем длину волны по заданной частоте ƒ = 4 ГГц: 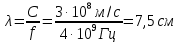 , (1) , (1)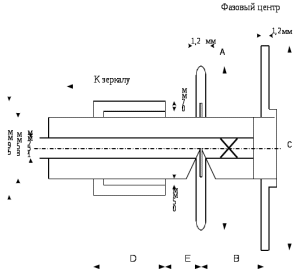 Рис. 1. Конструкция вибраторного облучателя [1]. Определим геометрические размеры облучателя, в соответствии с обозначениями на рис. 1: A=0,47·λ=0,03525м=3,525см, B=0,19·λ=0,01425м=1,425см, C=0,8·λ=0,06м=6см, D=0,24·λ=0,018м=1,8см, E=0,16·λ=0,012м=1,2см. Радиус раскрыва и угол раскрыва зеркала (угол между фокальной осью и прямой, проведенной из фокуса к кромке параболоида) связаны соотношением [2]: 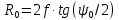 , (2) , (2)Форма зеркала обычно характеризуется отношением R0/f0 или половиной угла раскрыва ψ0. На рис. 2 показано положение фазового центра облучателя. 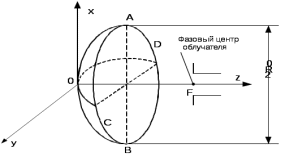 Рис. 2. Зеркальная параболическая антенна Радиус раскрыва рефлектора задан из условия задания: R0 = 50 м, Введем понятие эффективности зеркальной антенны g – это произведение КПД антенны на ее КИП. На рис. 3 показан график зависимости эффективности антенны от угла раскрыва [3], где n – любое положительное число. 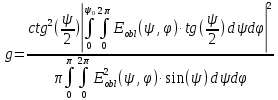 , (3) , (3)где 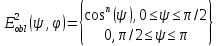 , (4) , (4)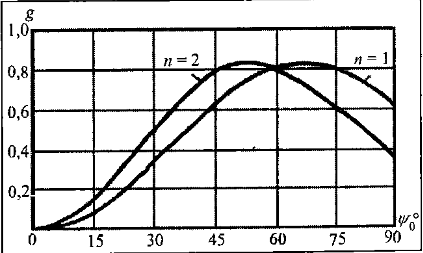 Рис. 3. Зависимость эффективности антенны от угла раскрыва [3]. На рис. 4 приведена зависимость коэффициента полезного действия η, коэффициента использования поверхности ν и эффективности зеркальной антенны gот угла раскрыва ψ [3]. 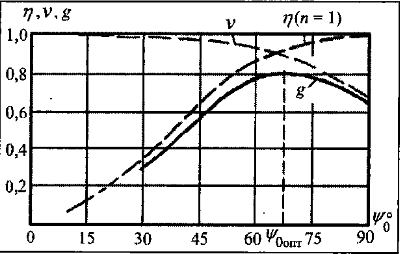 Рис. 4. Зависимость КПД, КИП и эффективности зеркальной антенны от угла раскрыва [3]. Как следует из рис. 4 существует оптимальный угол раскрыва при котором эффективность, используя формулу (3) найдем оптимальный угол раскрыва, который в нашем случае лежит в интервале 70° – 80° (рис. 5). Получаем ψ = 77°. Тогда оптимальное фокусное расстояние равно 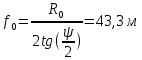 , (5) , (5)Глубина зеркала определяется по формуле 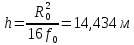 , (6) , (6)Найдем другие характеристики антенны При n = 1, получаем 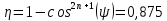 , (7) , (7)Максимальная эффективность достигает 0,82 (см. рис. 3). На практике затенение облучателя и системы крепления, кроссполяризационные потери и ряд других эффектов приводят к уменьшению эффективности до 0,4 – 0,8, поэтому примем g = 0,8. КИП антенны полностью определяется характером распределения поля в раскрыве зеркала. С увеличением ψ увеличивается спадание амплитудного распределения к краям зеркала и поэтому коэффициент использования поверхности уменьшается с увеличением угла раскрыва. 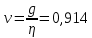 , (8) , (8)Уравнение параболы имеет вид: 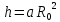 , отсюда , отсюда 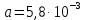 Геометрическая площадь рефлектора антенны равна 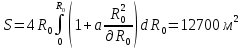 , (9) , (9)Эффективная площадь антенны 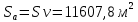 , (10) , (10)Коэффициент усиления апертурной антенны 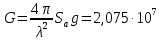 , (11) , (11)Коэффициент направленного действия антенны 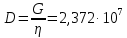 . (12) . (12)Характеристика направленности облучателя с рефлектором может быть определенна по формулам (13–14) [4], построим графики ДН в программе MathCAD: 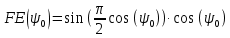 – в плоскости Е, (13) – в плоскости Е, (13)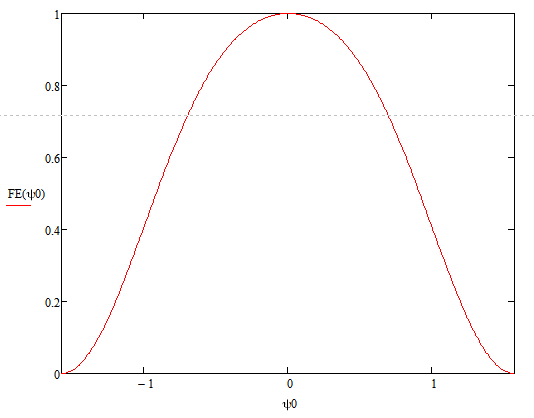 Рис. 5. Нормированная характеристика направленности облучателя в плоскости Е. 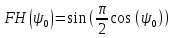 – в плоскости Н, (14) – в плоскости Н, (14)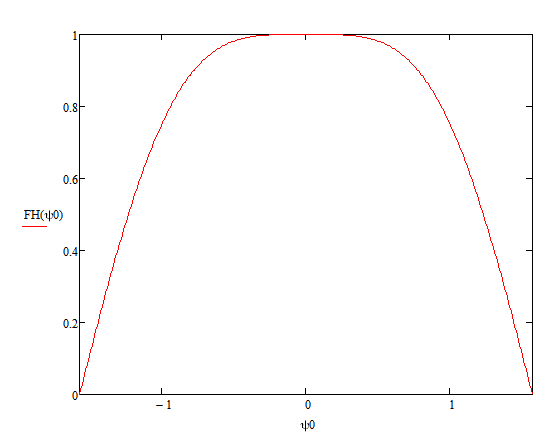 Рис. 6. Нормированная характеристика направленности облучателя в плоскости Н. Для расчёта излучения параболических антенн был использован апертурный метод. Амплитудное распределение в раскрыве зеркала определяется формой зеркала (отношением R0/f0) и ДН облучателя. При расчете амплитудного распределения полагают, что зеркало относительно облучателя находится в дальней зоне. Это допустимо, так как расстояние от фокуса до поверхности зеркала составляет десятки длин волн. В этом случае относительная амплитуда напряженности поля, создаваемого облучателем в любой точке поверхности зеркала. 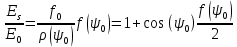 , (15) , (15)где Es – амплитуда напряженности поля в произвольной точке раскрыва зеркала; E0 – амплитуда напряженности поля у вершины зеркала; 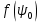 – нормированная характеристика направленности облучателя; – нормированная характеристика направленности облучателя;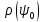 – расстояние от фокуса до любой точки внутренней поверхности параболоида; – расстояние от фокуса до любой точки внутренней поверхности параболоида;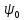 – угол под которым облучается элементарная площадка. – угол под которым облучается элементарная площадка.Отношение Es\E0 – приближенное амплитудное распределение возбуждающего поля, которое удобно изображать в виде графика и рассматривать как функцию относительного переменного радиуса раскрыва в плоскости Е (рис. 7): 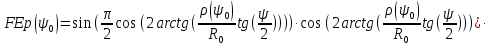 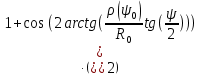 , (16) , (16)Однако представление амплитудного распределения в виде точной аналитической функции f1(/R0) либо невозможно, либо приводит к громоздким вычислениям при расчете диаграммы направленности. 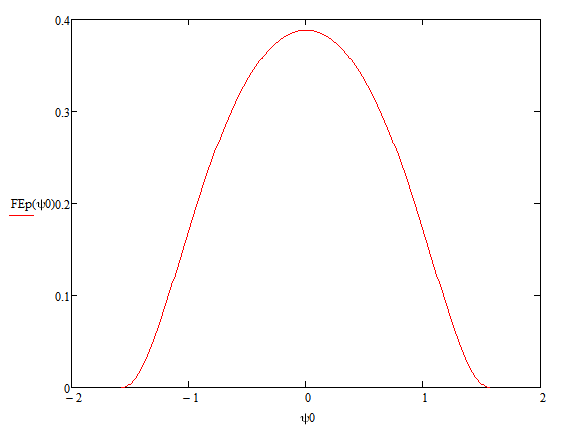 Рис. 7. График функции амплитудного распределения возбуждающего поля в раскрыве в плоскости Е. В случае осесимметричной или мало отличающейся от нее диаграммы направленности облучателя хорошие результаты дает аппроксимация функции f1(/R0) степенным рядом: 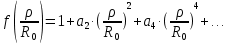 , (17) , (17)При этом для практических расчетов можно ограничиться только первыми тремя членами ряда. В этом случае диаграмма направленности облучателя будет выражаться следующим образом: 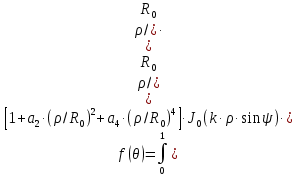 , (18) , (18)После интегрирования получаем: 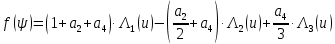 , (19) , (19)где  ; ;  – лямбда - функции. – лямбда - функции.Для расчета диаграммы направленности необходимо определить коэффициенты а2 и а4 . Необходимо провести аппроксимацию амплитудного распределение в раскрыве зеркала. Аппроксимация сводится к подбору коэффициентов а2 и а4 так, чтобы аппроксимирующая функция f(/R0) совпадала с функцией амплитудного распределения f1(/R0) в двух точках, например при /R0 = 1 и при /R0 = 0,9 (в точке /R0 = 0 совпадение функции f1(/R0) с функцией f(/R0) выполняется автоматически). Пусть при /R0 = 1 f1(/R0) = 1 и при /R0 = 0,9 f1(/R0) = 2. Тогда получим следующие соотношения:  , (20) , (20)Зная амплитудное распределение в раскрыве зеркала, рис. 7, найдём параметры 1 и 2 при соответствующих значениях /R0. Так при /R0 = 1:  ; ;при /R0 = 0,9: 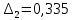 . .Теперь решим следующую систему уравнений (20) и определим коэффициенты а2 и а4: а2 = – 1,056; а4 = 0,321. После определения необходимых коэффициентов можно записать выражение для диаграммы направленности антенны: 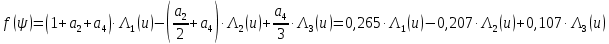 , (21) , (21)Лямбда-функция связана с функцией Бесселя следующим соотношением: 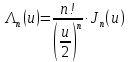 , (22) , (22)где 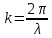 – волновое число; – волновое число;Учитывая данные соотношения можно записать окончательное выражение для диаграммы направленности антенны: 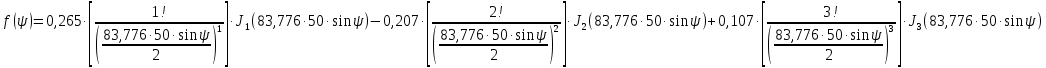 , (23) , (23)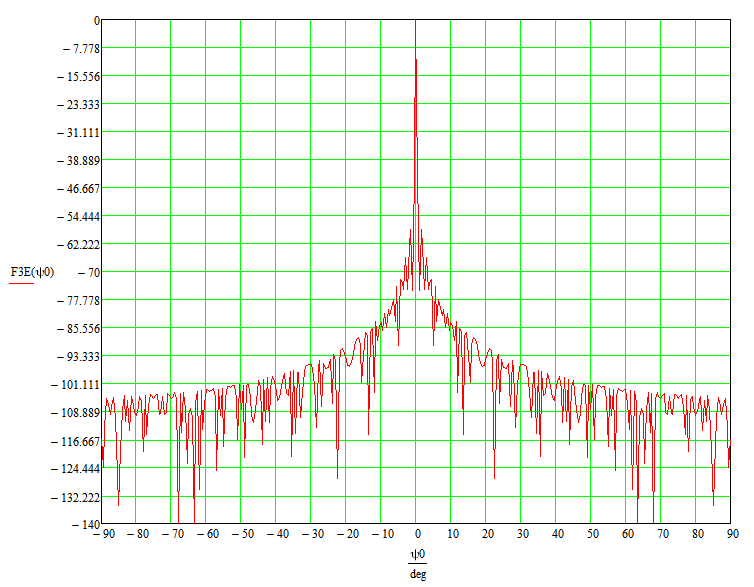 Рис. 8. Нормированная диаграмма направленности антенны без учета затенения в плоскости Е. Еще одним из основных параметров антенны является ширина главного лепестка в главных плоскостях. Значения этого угла можно определить по ДН, которая построена для данной антенны. Диаграмма направленности антенны с учетом затенения определяется по следующей формуле: 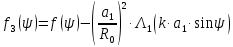 , (24) , (24)где а1 – радиус раскрыва облучателя. После подстановки значений получаем 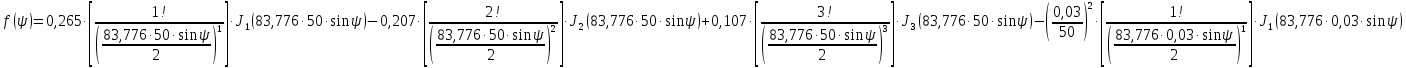 , (25) , (25) Рис. 9. Нормированная диаграмма направленности антенны с учетом затенения в плоскости Е. Построим теперь диаграмму направленности антенны в плоскости Н. Отношение Es\Е0 – приближенное амплитудное распределение возбуждающего поля, которое удобно изображать в виде графика и рассматривать как функцию относительного переменного радиуса раскрыва /R0 в плоскости H (рис. 10): 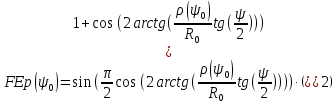 , (26) , (26)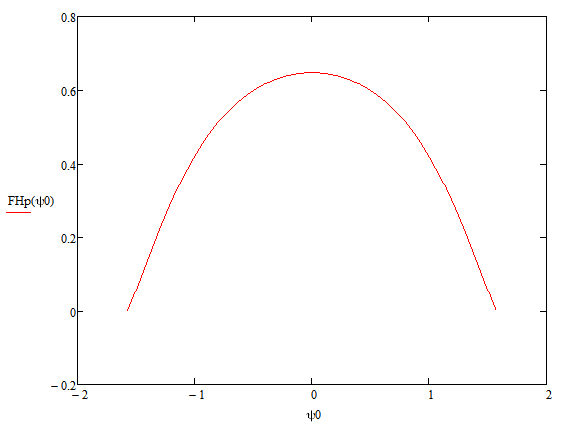 Рис. 10. График функции амплитудного распределения возбуждающего поля в раскрыве в плоскости H. В случае осесимметричной или мало отличающейся от нее диаграммы направленности облучателя хорошие результаты дает аппроксимация функции f1(/R0) степенным рядом по формуле (17). Для расчета диаграммы направленности необходимо определить коэффициенты а2 и а4 . Необходимо провести аппроксимацию амплитудного распределение в раскрыве зеркала. Аппроксимация сводится к подбору коэффициентов а2 и а4 так, чтобы аппроксимирующая функция f(/R0) совпадала с функцией амплитудного распределения f1(/R0) в двух точках, например при /R0 = 1 и при /R0 = 0,9 (в точке /R0 = 0 совпадение функции f1(/R0) с функцией f(/R0) выполняется автоматически). Пусть при /R0 = 1 f1(/R0) = 1 и при /R0 = 0,9 f1(/R0) = 2. Тогда получим следующие соотношения (20). Зная амплитудное распределение в раскрыве зеркала, рис. 6, найдём параметры 1 и 2 при соответствующих значениях /R0. Так при /R0 = 1: 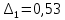 ; ;при /R0 = 0,9: 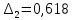 . .Теперь решим систему уравнений (20) и определим коэффициенты а2 и а4: а2 = – 0,478; а4 = 0,0088. После определения необходимых коэффициентов можно записать выражение для диаграммы направленности антенны: 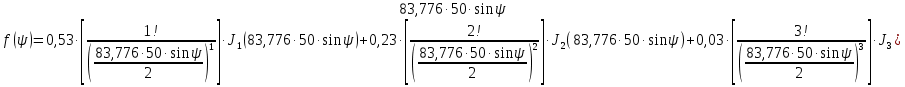 , (27) , (27)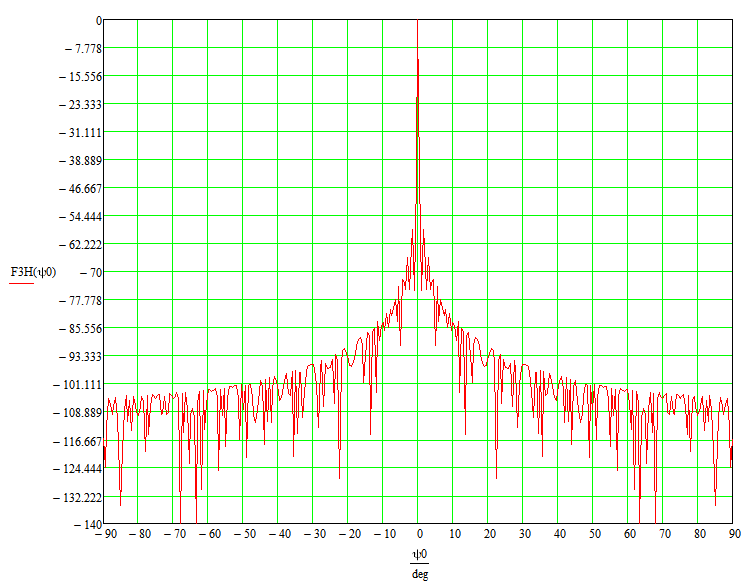 Рис. 11. Нормированная диаграмма направленности антенны без учета затенения в плоскости Н. Радиус раскрыва облучателя определяется самой большой его частью, т.е радиусом дискового рефлектора, отсюда, a1=0,03м. Диаграмма направленности антенны с учетом затенения определяется по формуле (24). 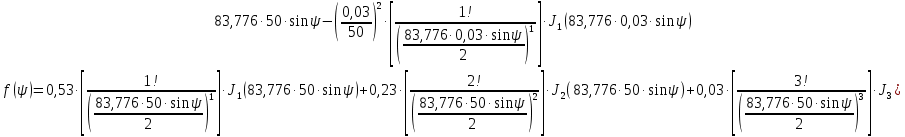 , (28) , (28) Рис. 12. Нормированная диаграмма направленности антенны с учетом затенения в плоскости Н. Диаграмма направленности с учетом затенения изменилась не значительно, в частности боковые лепестки остались на том же уровне, по сравнению с ДН без учета затенения. Это объясняется очень малым отношением диаметра облучателя к диаметру раскрыва. Профиль зеркала определяется формулой: 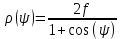 , (29) , (29)Построим зависимость 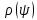 в секторе углов. в секторе углов.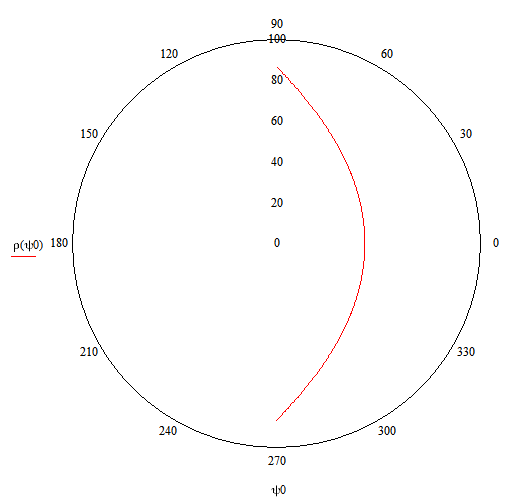 Рис. 13. Профиль рефлектора антенны. Пусть поверхность параболоида имеет некоторые неровности (рис. 14) (выступы и углубления). Наибольшее отклонение от идеальной поверхности определяется формулой: 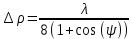 , (30) , (30)Анализ полученного выражения для 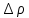 показывает, что вблизи центра параболоида показывает, что вблизи центра параболоида 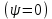 необходимая точность изготовления зеркала наивысшая. Здесь наибольшее отклонение от идеальной поверхности не должно превосходить величины 𝜆/16, у кромки параболоида требования к точности получаются наименьшими. необходимая точность изготовления зеркала наивысшая. Здесь наибольшее отклонение от идеальной поверхности не должно превосходить величины 𝜆/16, у кромки параболоида требования к точности получаются наименьшими. Для центра параболоида: 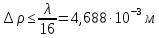 , ,У кромки параболоида: 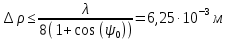 , ,Смещение фазового центра из фокуса вдоль оси приводит к симметричным квадратичным фазовым ошибкам в раскрыве зеркала. Его ДН при этом расширяется и даже раздваивается, а боковые лепестки возрастают. Но форма ДН остается симметричной. Допустимое смещение вдоль оси зеркала определяется: 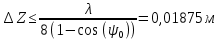 . (31) . (31)При смещении фазового центра в сторону от оси на угол α вся ДН отклонится от оптической оси на такой же угол α в сторону, противоположную смещению облучателя. Для зеркал средней глубины (ψ0=60°–90°) приближенно можно считать, что ДН искажается незначительно. Допустимое смещение определяется по формуле: 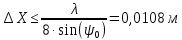 , (32) , (32)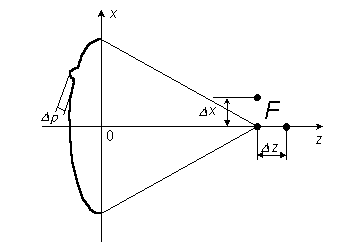 Рис. 14. Расположение допусков на точность изготовления антенны. Список использованной литературы Сазонов, Д.М. Антенны и устройства СВЧ [Текст]: учебник для радиотехнич. спец. вузов / Д.М. Сазонов. – М.: Высш. шк., 1988. – 432 с. Кочержевский, Г.Н. Антенно-фидерные устройства [Текст]: учебник для вузов / Г.Н. Кочержевский, Г.А. Ерохин, Н.Д. Козырев. – М.: Радио и связь, 1989. – 352 с. Устройства СВЧ и антенны [Текст]: учебник для вузов / Д.И. Воскресенский [и др.]; под ред. Д.И. Воскресенский. – М.: изд-во Радиотехника, 2006. – 375с. Заикин, И.П. Проектирование антенных устройств СВЧ [Текст] / И.П. Заикин, А.В. Тоцкий, В.В. Лукин. – Харьков: Нац. Аэрокосм. ун–т «Харьк. авиац. ин–т », 2005. – 107 с. |
