детали машин. детали машин 2. Рис Схема привода Выбор материалов, термообработки и допускаемых напряжений
 Скачать 61.98 Kb. Скачать 61.98 Kb.
|
|
Исходные данные: схема привода ленточного конвейера (рисунок 1), необходимое тяговое (окружное) усилие на барабане  . Срок службы привода – 5 лет. Режим работы пятидневный, двухсменный, средний равновероятный. Привод нереверсивный, степень точности изготовления колёс – 6-я. Допускается кратковременная 2-кратная перегрузка. Частоты вращения шестерни и колеса: . Срок службы привода – 5 лет. Режим работы пятидневный, двухсменный, средний равновероятный. Привод нереверсивный, степень точности изготовления колёс – 6-я. Допускается кратковременная 2-кратная перегрузка. Частоты вращения шестерни и колеса:  , , 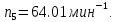 Передаточное отношение равно 2. Вращающие моменты на валах шестерни и колеса Передаточное отношение равно 2. Вращающие моменты на валах шестерни и колеса  , ,  соответственно. соответственно. Рис.1. Схема привода Выбор материалов, термообработки и допускаемых напряжений. Т Для изготовления колеса и шестерни выбираем сталь 40Х. Назначаем термообработку: Для колеса – улучшение до 230…260 НВ; Для шестерни – азотирование поверхности зубьев до твердости поверхности 50…59 HRC (твёрдость сердцевины зуба 26…30 HRC). Допускаемые контактные напряжения определяем по формуле 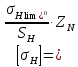 , (1) , (1)где  – предел контактной выносливости зубьев, МПа; – предел контактной выносливости зубьев, МПа;  – коэффициент долговечности; – коэффициент долговечности;  – коэффициент безопасности. – коэффициент безопасности.Принимаем  ; ; . .Предел контактной выносливости  : :Для шестерни  . .Для колеса  Коэффициент долговечности 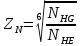 , (2) , (2)Где 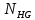 – базовое число циклов; – базовое число циклов; 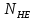 – эквивалентное число циклов. – эквивалентное число циклов.Находим базовое число циклов  : : (3) (3)Базовое число циклов  определяем, предварительно найдя среднее значение в единицах по Рокуэллу: определяем, предварительно найдя среднее значение в единицах по Рокуэллу: (4) (4)Так как 54,5 HRC = 540 HB, то:  Расчёт работы передачи в часах 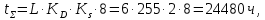 (5) (5)где  – количество рабочих дней в году; – количество рабочих дней в году;  – количество смен; L – срок службы. – количество смен; L – срок службы.Эквивалентное число циклов для шестерни  , (6) , (6)Где  – коэффициент режима работы; с – количество колёс, находящихся в зацеплении с данным колесом(шестерней). – коэффициент режима работы; с – количество колёс, находящихся в зацеплении с данным колесом(шестерней).Для колеса  . (7) . (7)Вычисляем коэффициенты долговечности для шестерни и колеса:  ; ;  . .Принимаем  и и 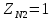 . .Допускаемые контактные напряжения для шестерни и колеса:  835,99 МПа; 835,99 МПа;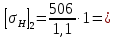 460 МПа. 460 МПа.Найдём среднее допускаемое напряжение:  (8) (8)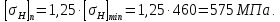 Принимаем  Допускаемые напряжения изгиба определяем по формуле 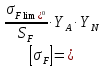 , (9) , (9)Где  – предел выносливости зубьев по напряжениям изгиба. МПа; – предел выносливости зубьев по напряжениям изгиба. МПа;  – коэффициент безопасности; – коэффициент безопасности;  – коэффициент, учитывающий влияние двухстороннего приложения нагрузки; – коэффициент, учитывающий влияние двухстороннего приложения нагрузки; 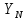 – коэффициент долговечности. – коэффициент долговечности.Предел выносливости по напряжениям изгиба  : :Для шестерни  Где  – средняя твёрдость сердцевины шестерни, в данном случае: – средняя твёрдость сердцевины шестерни, в данном случае: . (10) . (10)Тогда 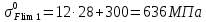 . . , ,Где  – среднее значение твёрдости сердцевины колеса в единицах Бринелля. – среднее значение твёрдости сердцевины колеса в единицах Бринелля.Коэффициент долговечности определяем по формуле  , (11) , (11)Где  – базовое число циклов; – базовое число циклов;  – эквивалентное число циклов; – эквивалентное число циклов; 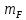 – показатель степени, зависящий от термообработки (здесь для шестерни – показатель степени, зависящий от термообработки (здесь для шестерни  и для колеса и для колеса  ). ).Эквивалентное число циклов перемены напряжений изгиба для шестерни 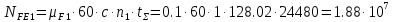 , (12) , (12)Где  – коэффициент режима работы для шестерни при действии напряжений изгиба. Здесь – коэффициент режима работы для шестерни при действии напряжений изгиба. Здесь  – для шестерни; – для шестерни; 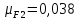 – для колеса. – для колеса.Эквивалентное число циклов для колеса 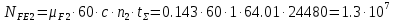 , (13) , (13)Коэффициенты долговечности для шестерни и колеса  ; ;  Принимаем  ; ;  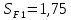 ; ;  . . ; ;  . .Для шестерни  Для колеса  Максимальные допускаемы напряжения изгиба  , (14) , (14)Где  – максимальная величина коэффициента долговечности; – максимальная величина коэффициента долговечности; 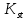 – коэффициент учёта частоты приложения пиковой нагрузки. – коэффициент учёта частоты приложения пиковой нагрузки.При твёрдости поверхности колёс НВ>350  = 2,5, = 2,5,  . .При твёрдости поверхности колёс НВ≤350  = 4, = 4,  . .Таким образом, для шестерни и колеса 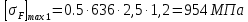 ; ; ; ;Проектный расчёт цилиндрической косозубой передачи Принимаем  Коэффициент ширины колеса относительно делительного диаметра  . (16) . (16)Максимально допустимое  не превышено. не превышено.Выбираем   , (31) , (31)Где С – коэффициент твёрдости и типа зубьев, С=0,25;  – степень точности изготовления колёс, – степень точности изготовления колёс,  ; ;  – допускаемое значение – допускаемое значение  , для косозубых передач , для косозубых передач  =1,6. =1,6. Определяем межосевое расстояние:    160 мм 160 ммОпределяем ширину зубчатых колёс:  (17) (17)Принимаем ширину колеса  . Ширину колеса увеличиваем, . Ширину колеса увеличиваем,  . .Модуль передачи (в нормальном сечении) принимаем по формуле  , (18) , (18)Где 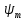 – коэффициент модуля. – коэффициент модуля.Принимаем  . Тогда . Тогда . .Принимаем стандартный модуль  =1.25 мм. =1.25 мм.Находим суммарное число зубьев по формуле:   Определим число зубьев шестерни и колеса:  ; ;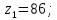 z2=z-  . .Уточняем передаточное число:  (23) (23)Определяем геометрические параметры передачи, необходимые для проверочного расчёта. Делительные диаметры шестерни и колеса: d1=m* 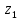 =1.25*86=107.5 мм =1.25*86=107.5 ммd2=m*  =1.25*170=212.5 мм =1.25*170=212.5 ммПроверочные расчёты цилиндрической прямозубой передачи Выполняем проверочный расчёт передачи по контактным напряжениям. Условие прочности записываем следующим образом:  (26) (26)Где  – момент на шестерне; – момент на шестерне;  – коэффициент повышения прочности косозубых передач по контактным напряжениям; – коэффициент повышения прочности косозубых передач по контактным напряжениям;  – модуль упругости, для стальных зубчатых колёс – модуль упругости, для стальных зубчатых колёс 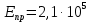  – коэффициент расчётной нагрузки. – коэффициент расчётной нагрузки.Рассчитываем коэффициент перекрытия коэффициенты перекрытия. Для нефланкированных передач без смещения коэффициент торцового перекрытия  (27) (27)Коэффициент расчётной нагрузки  , (30) , (30)Где  – коэффициент распределения нагрузки между зубьями; – коэффициент распределения нагрузки между зубьями;  =1,05; =1,05;  – коэффициент динамической нагрузки. – коэффициент динамической нагрузки.Коэффициент распределения нагрузки между зубьями находи по формуле  , (31) , (31)Где С – коэффициент твёрдости и типа зубьев, С=0,25;  – степень точности изготовления колёс, – степень точности изготовления колёс,  ; ;  – допускаемое значение – допускаемое значение  , для косозубых передач , для косозубых передач  =1,6. =1,6. Для определения коэффициента динамической нагрузки  необходимо знать окружную скорость необходимо знать окружную скорость  . . . (32) . (32)Принимаем 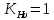 . .Тогда 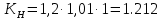 Таким образом  (33) (33) Условие прочности выполняется. Недогрузка составляет:  (34) (34)Недогрузка является допустимой, так как не превышает  . .Выполняем проверочный расчёт прочности передачи по напряжениям изгиба:  , (35) , (35)Где  – окружная сила; – окружная сила;  – коэффициент расчётной нагрузки по напряжениям изгиба; – коэффициент расчётной нагрузки по напряжениям изгиба;  – коэффициент формы зуба; – коэффициент формы зуба;  – коэффициент повышения прочности прямозубых передач по напряжениям изгиба. – коэффициент повышения прочности прямозубых передач по напряжениям изгиба. ; ; ; ;Выбираем коэффициент формы зуб  ; ;(36)  При нулевом суммарном смещении для шестерни  3,76; для колеса 3,76; для колеса  Для шестерни и для колеса находим отношение Для шестерни и для колеса находим отношение  . .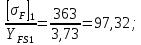  . (37) . (37)Дальнейший расчёт ведём по колесу, т.к данное соотношение меньше. То есть принимаем 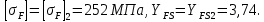 Коэффициент повышения прочности прямозубых передач по напряжениям изгиба  =1,12. (38) =1,12. (38)Коэффициент расчётной нагрузки  по напряжениям изгиба определяется по напряжениям изгиба определяется , (39) , (39)Где  – коэффициент распределения нагрузки между зубьями; – коэффициент распределения нагрузки между зубьями;  – коэффициент концентрации нагрузки; – коэффициент концентрации нагрузки; 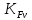 – коэффициент динамической нагрузки. – коэффициент динамической нагрузки.Принимаем 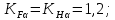 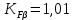 ; ;  . .Таким образом 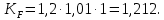 По формуле 35 напряжения изгиба  Изгибная прочность передачи обеспечена. Недогрузка составляет:  (34) (34)Недогрузка является допустимой, так как не превышает 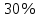 . .Выполняем проверочный расчёт на заданную перегрузку. Согласно исходным данным допускается трёхкратная перегрузка (  ). ).Тогда максимальные контактные напряжения  (40) (40)Максимальные напряжения изгиба по передаче (по наиболее слабому элементу - колесу)  (41) (41)Так как выполняются оба условия – прочность при перегрузках обеспечена. Определяем недостающие геометрические параметры для построения чертежа шестерни и колеса. Диаметры вершин зубьев шестерни и колеса соответственно 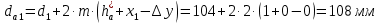 ; (42) ; (42) , (43) , (43)Где  - коэффициент высоты головки зуба, - коэффициент высоты головки зуба,  ; ;  – коэффициент уравнительного смещения, определяемый по ГОСТ 16532-70 ( – коэффициент уравнительного смещения, определяемый по ГОСТ 16532-70 ( для передач с колёсами без смещения, для передач с колёсами без смещения,  ). ).Диаметры впадин зубьев шестерни и колеса соответственно  ; (44) ; (44) ; (45) ; (45)Где  - коэффициент радиального зазора, - коэффициент радиального зазора, 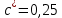 . .Таблица. Параметры зубчатой передачи
| |||||||||||||||||||||||||||||||||

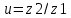


 , мм
, мм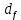 , мм
, мм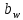 , мм
, мм , мм
, мм