Редуктор. Пояснительная записка. Рисунок 1 Кинематическая схема привода
 Скачать 1.05 Mb. Скачать 1.05 Mb.
|
|
4. Расчет тихоходной внутренней косозубой передачи 4.1 Выбор твёрдости, термообработки и материала колёс тихоходной зубчатой передачи Выберем материал для зубчатой пары колёс, одинаковый для шестерни и колеса, но с разными твёрдостями, так как твёрдость зубьев шестерни должна быть больше твёрдости зубьев колеса Принимаем для шестерни – 40Х и для колеса - 45 [4]. Выберем термообработку для зубьев шестерни - улучшение и для зубьев колеса - улучшение. Выберем интервал твёрдости зубьев шестерни HB3 = 269…302 HB и колеса HB4 = 235…262 HB. Определяем среднюю твёрдость зубьев шестерни HB3ср и колеса HB4ср 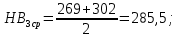 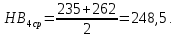 Определяем разность средних твёрдостей зубьев шестерни и колеса 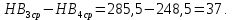 При этом соблюдается необходимая разность средних твёрдостей зубьев шестерни и колеса. Определяем механические характеристики сталей для шестерни и колеса: - для шестерни 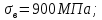 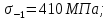 - для колеса 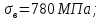 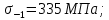 По таблице 3.2 [4] выбираем предельные значения размеров заготовки шестерни (Dпред - диаметр) и колеса (Sпред - толщина обода или диска): - для шестерни Dпред = 125 мм, - для колеса Sпред = 80 мм. Определяем допускаемые контактные напряжения Определяем коэффициент долговечности для зубьев шестерни KHL3 и колеса KHL4 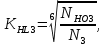 (4.1) (4.1)где NHO3=10·106 циклов – число циклов перемены напряжений, соответствующее пределу выносливости [4]; N3 – число циклов перемены напряжений за весь срок службы 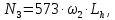 (4.2) (4.2)где ω2 - угловая скорость быстроходного вала, 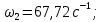 Lh=18000 ч. – срок службы привода; 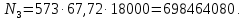 Т.к. 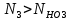 , то принимаем KHL3 = 1. , то принимаем KHL3 = 1.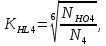 (4.3) (4.3)где NHO4=10·106 циклов – число циклов перемены напряжений, соответствующее пределу выносливости [4]; N4 – число циклов перемены напряжений за весь срок службы 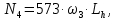 (4.4) (4.4)где ω3- угловая скорость тихоходного вала, 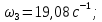 Lh= 18000 ч.– срок службы привода; 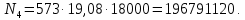 Т.к. 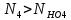 , то принимаем KHL4 = 1. , то принимаем KHL4 = 1.Определяем допускаемое контактное напряжение, соответствующее пределу выносливости при числе циклов перемены напряжений NHO3 и NHO4 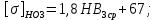 (4.5) (4.5)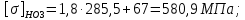 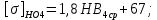 (4.6) (4.6)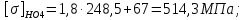 Определяем допускаемые контактные напряжения для зубьев шестерни и колеса 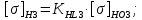 (4.7) (4.7)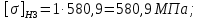 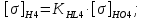 (4.8) (4.8)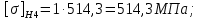 Расчет будем вести по наименьшему значению 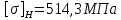 . .4.2 Расчет допускаемых напряжений изгиба Определяем коэффициент долговечности для зубьев шестерни KFL3 и колеса KFL4 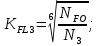 (4.9) (4.9)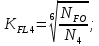 (4.10) (4.10)где N3 – число циклов перемены напряжений за весь срок службы. Т.к. N3>NFO и N4>NFO, то принимаем KFL3=KFL4 = 1. Определяем допускаемое напряжение изгиба соответствующее пределу изгибной выносливости при числе циклов перемены напряжений 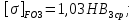 (4.11) (4.11)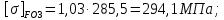 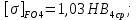 (4.12) (4.12)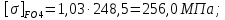 Определяем допускаемые напряжения изгиба для зубьев шестерни и колеса 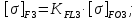 (4.13) (4.13)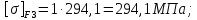 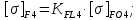 (4.14) (4.14)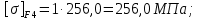 Расчет будем вести по наименьшему значению 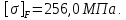 4.3 Проектный расчет закрытой цилиндрической зубчатой передачи Определяем межосевое расстояние 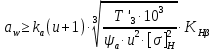 (4.15) (4.15)где u – передаточное число редуктора; T’3 = 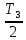 – вращающий момент на одной паре зацепления раздвоенной ступени, Н·м; – вращающий момент на одной паре зацепления раздвоенной ступени, Н·м; ; ;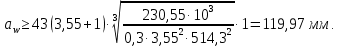 Полученное значение внешнего делительного диаметра округляем до ближайшего по стандартному ряду до Определяем модуль зацепления 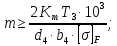 (4.16) (4.16)где d4- делительный диаметр колеса. 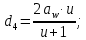 (4.17) (4.17)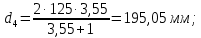 b4- ширина венца колеса; 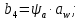 (4.18) (4.18)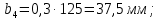 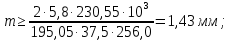 Полученное значение модуля округляем до стандартного, получаем m =1,5 мм. Определяем угол наклона зубьев β косозубой передачи 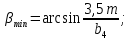 (4.19) (4.19)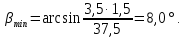 Определяем суммарное число зубьев шестерни и колеса 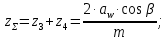 (4.20) (4.20)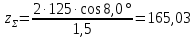 ; ;Полученное значение округляем до целого числа и берём 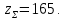 Определяем число зубьев шестерни 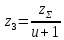 ; (4.21) ; (4.21)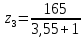 =36,26. =36,26. Округляем полученное значение до целого, получаем 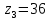 . .Определяем число зубьев колеса 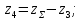 (4.22) (4.22)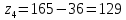 . . Определяем фактическое передаточное число uф и проверяем его отклонение 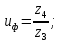 (4.23) (4.23)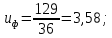  (4.24) (4.24)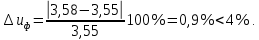 Определяем фактический угол наклона зубьев 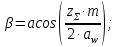 (4.25) (4.25)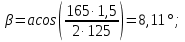 Определяем фактические основные геометрические параметры передачи для шестерни и колеса: - делительный диаметр шестерни и колеса 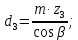 (4.26) (4.26)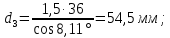 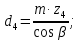 (4.27) (4.27)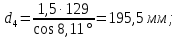 - диаметр вершин зубьев шестерни и колеса 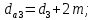 (4.28) (4.28)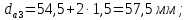 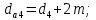 (4.29) (4.29)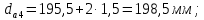 - диаметр впадин зубьев шестерни и колеса 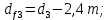 (4.30) (4.30)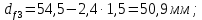 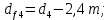 (4.31) (4.31)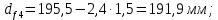 - ширина венца шестерни и колеса 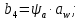 (4.32) (4.32)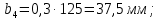 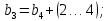 (4.33) (4.33)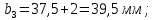 Округляем значения ширины венца колеса до ближайшего по стандартному ряду, принимаем b3 = 40 мм и b4 = 38 мм 4.4 Проверочный расчет закрытой цилиндрической зубчатой передачи Проверяем межосевое расстояние 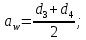 (4.34) (4.34)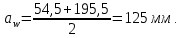 Проверяем пригодность заготовок колёс. Условие пригодности заготовок колёс Диаметр заготовки шестерни 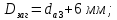 (4.37) (4.37)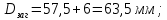 Толщина диска колеса 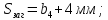 (4.38) (4.38)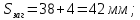 Проверяем условия пригодности (4.35) и (4.36) 63,5<125 мм; 42< 80 мм. Условия прочности выполняются. Проверяем контактные напряжения 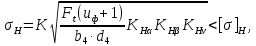 (4.39) (4.39)где К = 376 – вспомогательный коэффициент для косозубых колес [4]; 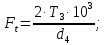 (4.40) (4.40)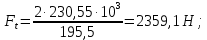 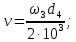 (4.41) (4.41)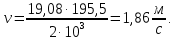 Принимаем степень точности 8, следовательно, по таблице 4.3 [4] Подставляя полученные значения в формулу (5.39), получаем 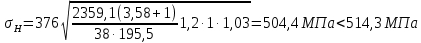 , ,  (4.42) (4.42)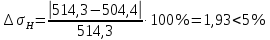 . .Условие прочности по контактным напряжениям выполняется. Проверяем напряжения изгиба зубьев колеса 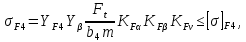 (4.43) (4.43)где YF3, YF4 – коэффициенты формы зуба шестерни и колеса, определяются по таблице 4.4 [4] в зависимости от эквивалентного числа зубьев шестерни и колеса, принимаем YF4 = 3,61 и YF3 = 3,74; 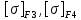 - допускаемые напряжения изгиба и шестерни; - допускаемые напряжения изгиба и шестерни;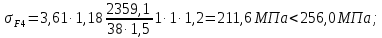 Допускается недогрузка по напряжениям изгиба. Проверяем напряжения изгиба зубьев шестерни 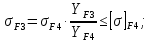 (4.44) (4.44)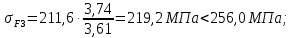 Допускается недогрузка по напряжениям изгиба. Условие прочности по напряжениям изгиба выполняется. Представим проектный и проверочный расчеты зубчатой передачи в виде таблиц (таблица 4.1 и таблица 4.2). Таблица 4.1 – Результаты расчет зубчатой цилиндрической передачи тихоходной ступени редуктора
Таблица 4.2 – Проверочный расчет зубчатой цилиндрической передачи тихоходной ступени редуктора
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
