Зернова Д.А._Теория вероятности_ИПЗ. Российский государственный социальный университет ипз по дисциплине Теория вероятности
 Скачать 85.19 Kb. Скачать 85.19 Kb.
|
ИПЗ по дисциплине «Теория вероятности»
Москва Вариант 23 1.Сколько различных «слов» можно получить, если переставлять буквы в слове «ПАРАЛЛЕЛОГРАММ»? («словом» называется любая последовательность букв, не обязательно осмысленная) П-1 А-3 Р-2 Л-3 Е-1 О-1 Г-1 М-2 M=14 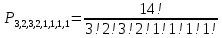 = 139708800 = 1397088002. В лотерее 100 билетов. Из них 50 выигрышные, остальные 50 невыигрышные. Куплено три билета. Какова вероятность того, что все купленные билеты – выигрышные? 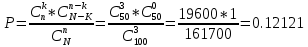 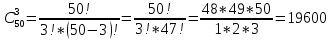 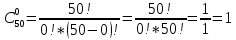 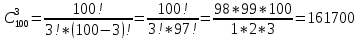 3.У Насти 15 книг, из них 6 на испанском языке. Настя взяла наудачу 8 книг. Найти вероятность того, что книги на испанском языке она взяла все. Общее число 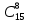 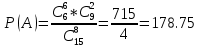 4.Три стрелка стреляют по цели. Вероятность попадания в цель первым – 0,65; вторым – 0,7; третьим – 0,75. Определить вероятность того, что при одновременном залпе тремя стрелками будет хотя бы одно попадание в цель. 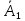 – (вероятность попадания в мишень i-м стрелком) , где i=1,2,3 – (вероятность попадания в мишень i-м стрелком) , где i=1,2,3Вероятность этих событий 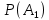 = 0,65; = 0,65; 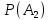 = 0,7; = 0,7; 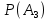 = 0,75 = 0,75 И противоположные им события: 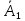 – (вероятность промаха i-м стрелком), где i=1,2,3 – (вероятность промаха i-м стрелком), где i=1,2,3Вероятность этих событий 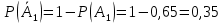 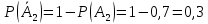 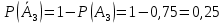 События B – (хотя бы один стрелок попадает в мишень) и 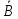 - (все три стрелка промахнуться) противоположные , - (все три стрелка промахнуться) противоположные , 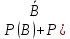 )=1 )=1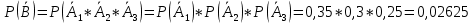 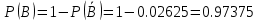 5.Монету бросают 7 раз. Найти вероятность того, что «герб=орел» выпадет менее двух раз. 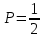 ; ; 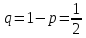 ; ; 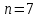 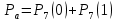 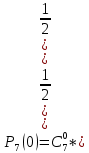 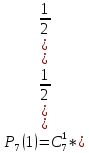 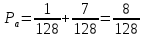 6. Контрольную работу по теории вероятностей успешно выполняют в среднем 70% студентов. Какова вероятность того, что из 200 студентов работу успешно выполнят не менее 100 человек? 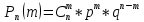 p=0,7- вероятность того, что случайно выбранный студент успешно выполнит контрольную q=1-p=1-0,7=0,3 – вероятность того, что случайно выбранный студент не выполнит контрольную 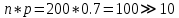 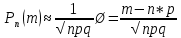 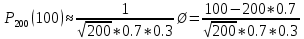 8.Дискретная случайная величина 𝜉 задана рядом распределения: 𝜉 -1 0 1 2 3 𝑃 0,1 0,2 𝑝 0,3 0,1 Найти: а) неизвестную вероятность 𝑝; б) функцию распределения 𝐹(𝑥) и построить её график; в) математическое ожидание𝑀[𝜉]; г) дисперсию 𝐷[𝜉]; д) 𝑃 (−1 ≤ 𝜉 <2). а) Таблица будет законом, если сумма вероятностей в нижней строке равна 1 0,1+0,2+р++0,3+0,1=1 Р=1-0,7=0,3 б) 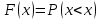 при 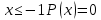 при 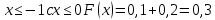 при 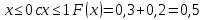 при 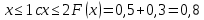 при 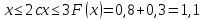 при 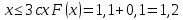    1,2   1   0,8 0,80,6   0,4   0,2 -3 -2 -1 1 2 3 4 в) 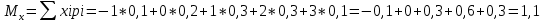 г) 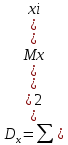 д) 𝑃 (−1 ≤ 𝜉 <2) = 0,3+0,3+1,1=1,7 10.Непрерывная случайная величина 𝜉 задана с помощью функции плотности распределения вероятностей𝑓(𝑥): 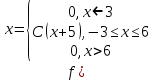 Найти: а) параметр 𝐶; б) функцию распределения 𝐹(𝑥) и построить ее график; в) математическое ожидание𝑀[𝜉]и дисперсию 𝐷[𝜉]; г) 𝑃 (0 <𝜉 ≤ 8). а) 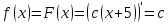 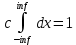 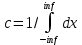 Интервал 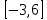 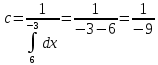 б) F(x) = x∫-∞f(x)dx F(x) = -3∫-∞0·dx = 0, x ≤ -3 F(x) = 1, x > 6 в) M[x] = b∫ax·f(x) dx D[x] = b∫ax2·f(x) dx - M[x]2 11.Случайная величина 𝜉 распределена равномерно на [0; 6]. Написать𝑓(𝑥) и 𝐹(𝑥). Найти 𝑀[𝜉] и 𝐷[𝜉]. Вычислить 𝑃 (−1 ≤ 𝜉 ≤ 4). 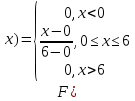 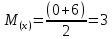 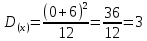 𝑃 (−1 ≤ 𝜉 ≤ 4) = F(4)-0=5/10 12.Случайная величина 𝜉 распределена нормально с математическим ожиданием 𝑀[𝜉] = 8 и дисперсией 𝐷 𝜉 = 36. Написать ее функцию плотности распределения вероятностей 𝑓(𝑥)и вычислить 𝑃 (1 ≤ 𝜉 ≤ 16) 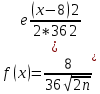 𝑃 (1 ≤ 𝜉 ≤ 16) =F (16)-F (1) = (16-1)/36-(1-1)/36 |

