Сапаева Мукаддас Курамбаевна_ИК__Алгебра. Российский государственный социальный университет Итоговый контроль по дисциплине Линейная алгебра
 Скачать 48.97 Kb. Скачать 48.97 Kb.
|
Итоговый контроль по дисциплине «Линейная алгебра»
Москва 2017 Уравнение плоскости Плоскость - есть поверхность, полностью содержащая, каждую прямую, соединяющую любые её точки. Это геометрическая фигура, состоящая из отдельных точек. Каждой точке в трехмерном пространстве соответствуют координаты, которые задаются тремя числами. Уравнение плоскости устанавливает зависимость между координатами всех точек. Уравнение плоскости в прямоугольной системе координат 0хуz имеет вид уравнения с тремя переменными х, у и z. Удовлетворяют уравнению координаты любой точки, лежащей в пределах заданной плоскости, не удовлетворяют координаты любых других точек, которые лежат вне заданной плоскости. Подстановка в уравнение плоскости координат точки данной плоскости, обращает уравнение в тождество. При подстановке координат точки, лежащей вне плоскости, уравнение превращается в неверное равенство. Уравнение плоскости может иметь несколько видов. В зависимости от специфики решаемых задач уравнение плоскости может быть записано по-разному. Общее уравнение плоскости Любую плоскость можно задать уравнением плоскости первой степени вида 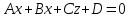 где A, B и C не могут быть одновременно равны нулю Нормальное уравнение плоскости – это общее уравнение плоскости вида 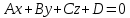 которое удовлетворяет следующим условиям: длина вектора 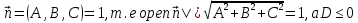 Также запись нормального уравнения плоскости может иметь следующий вид 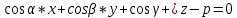 где 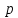 – это неотрицательное число, которое равно расстоянию от начала координат до плоскости, а – это неотрицательное число, которое равно расстоянию от начала координат до плоскости, а 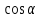 , , 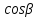 , , 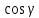 — это направляющие косинусы нормального вектора данной плоскости единичной длины. — это направляющие косинусы нормального вектора данной плоскости единичной длины.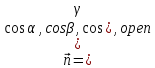 То есть, согласно нормальному уравнению плоскости, плоскость в прямоугольной системе координат 0хуz удалена от начала координат на расстояние 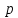 в положительном направлении нормального вектора этой плоскости в положительном направлении нормального вектора этой плоскости 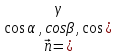 Если 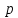 равно нулю, то плоскость проходит через начало координат. равно нулю, то плоскость проходит через начало координат.Уравнение плоскости в отрезках Если плоскость пересекает оси OX, OY и OZ в точках с координатами (a, 0, 0), (0, b, 0) и (0, 0, с), то она может быть найдена, используя формулу уравнения плоскости в отрезках 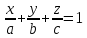 Уравнение прямой в пространстве Уравнение прямой на плоскости в прямоугольной системе координат 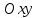 – это линейное уравнение с переменными – это линейное уравнение с переменными 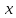 и и 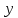 , которому отвечают координаты всех точек прямой и не удовлетворяют координаты никаких прочих точек. , которому отвечают координаты всех точек прямой и не удовлетворяют координаты никаких прочих точек.Если речь идет о прямой в трехмерном пространстве, все несколько иначе: не существует такого линейного уравнения с тремя переменными 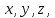 которому бы отвечали только координаты точек заданной прямой. которому бы отвечали только координаты точек заданной прямой. Уравнение прямой в пространстве как уравнение двух пересекающихся плоскостей: Когда две плоскости в пространстве имеют общую точку, существует их общая прямая, на которой находятся все общие точки этих плоскостей. Допустим, в трехмерном пространстве зафиксирована прямоугольная система координат 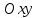 и задано, что прямая и задано, что прямая 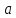 – это линия пересечения двух плоскостей α и β, которые соответственно описываются уравнениями плоскости – это линия пересечения двух плоскостей α и β, которые соответственно описываются уравнениями плоскости 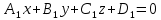 и и 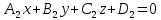 Поскольку прямая 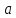 – это множество общих точек плоскостей α α и β β, то координаты любой точки прямой – это множество общих точек плоскостей α α и β β, то координаты любой точки прямой 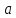 будут одновременно отвечать обоим уравнениям. Никакие прочие точки одновременно удовлетворять условия обоих уравнений не будут. будут одновременно отвечать обоим уравнениям. Никакие прочие точки одновременно удовлетворять условия обоих уравнений не будут.Таким образом, координаты любой точки прямой 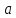 в прямоугольной системе координат станут частным решением системы линейных уравнений вида в прямоугольной системе координат станут частным решением системы линейных уравнений вида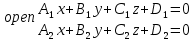 Общее же решение системы уравнений 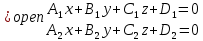 определит координаты каждой точки прямой 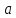 , те по сути задает саму прямую , те по сути задает саму прямую 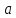 . .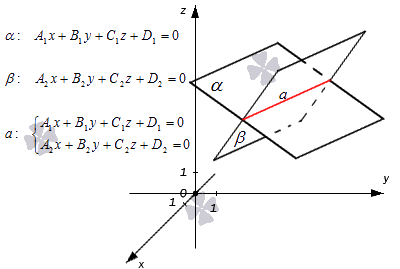 |

