ИИСА. ИИС РК4 Архипова К.С. Final (1). Российский государственный социальный университет Рубежный контроль к разделу 4 по дисциплине Интеллектуальные информационные системы
 Скачать 0.74 Mb. Скачать 0.74 Mb.
|
Рубежный контроль к разделу 4 по дисциплине «Интеллектуальные информационные системы» Работа с нечеткой логикой (тема практического задания)
Москва 2022 Лингвистическая переменнаяЛингвистическая переменная - используется в теории нечетких множеств и принимает значения фраз естественного или искусственного языка. Например лингвистическая переменная «скорость» может принимать значения «медленная», «средняя», «быстрая». Фразы значения которых принимает переменная являются в свою очередь именами нечетких переменных и описываются нечетким множеством. Задача с лингвистическими переменными В качестве примера задачи с лингвистическим переменными можно привести задачу из практического задания 4 где нам необходимо определить объем чаевых которые рекомендуется оставить официанту в зависимости от качества обслуживания и качества еды, при заданной оценке качества еды и обслуживания по 10 бальной шкале где 0 наихудшая и 10 наилучшая оценка. Для определения качества еды у нас будут использоваться лингвистические переменные «плохая» и «хорошая», для определения качества обслуживания будем использовать лингвистические переменные «плохое», «средне» и «отличное». Для определения размера чаевых определим лингвистические переменные «малые», «средние» и «щедрые». В среднем в ресторанах чаевые составляют 15% но эта величина может быть изменена в зависимости от оценки качества еды и обслуживания. Будем также предполагать, что у нас есть представления о малых чаевых, средних чаевых и щедрых. Мы хотим отобразить связь между двумя входами (качество еды и обслуживание) и выходом - количество чаевых. Чаевые должны быть щедрыми если еда и обслуживание были отличными иначе чаевые должны быть не высокими, при этом можно выделить некую плоскую область со значением 15%. Подход на базе нечеткой логики: Если еда и обслуживание плохие, то чаевые малые; Если еда и обслуживание среднее, то чаевые средние; Если еда и обслуживание хорошие, то чаевые большие. 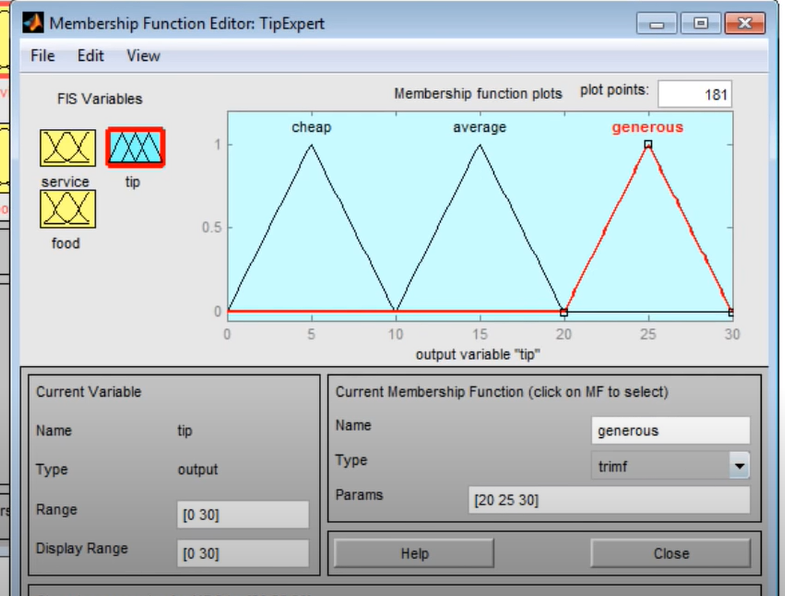 Рисунок 1 - Реализация в Fis Editor чаевые 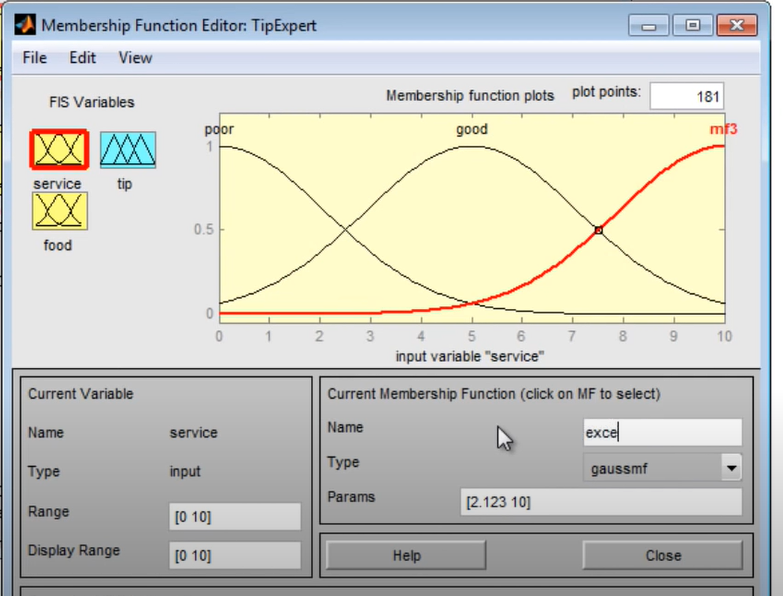 Рисунок 2 - Реализация в Fis Editor сервис 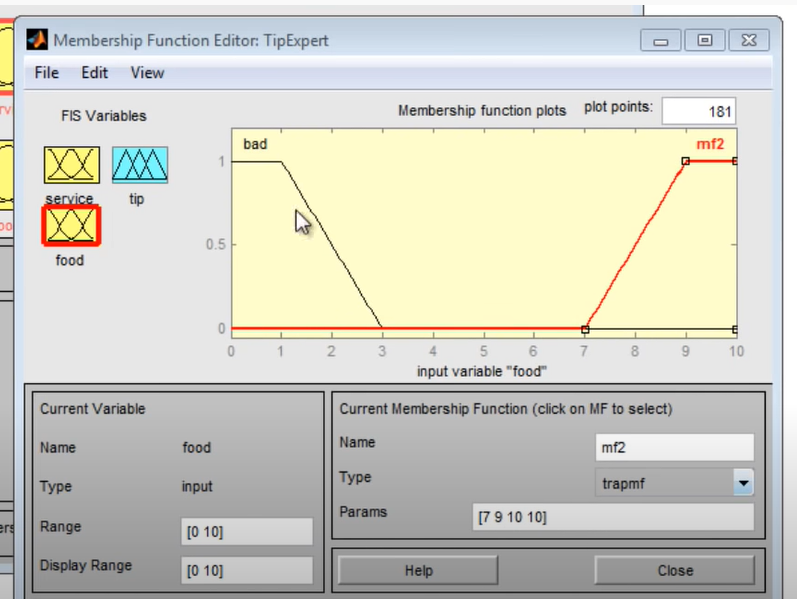 Рисунок 3 - Реализация в Fis Editor еда Привести пример реализации решения задачи, в которой используются лингвистические переменные на языках R, Python или др. Основные определения Прежде чем начать знакомство с алгоритмом важно кратко ознакомиться со следующими определениями: Нечеткая переменная — это кортеж вида <α, X, Α>, где: α — имя нечеткой переменной; X — её область определения; A — нечеткое множество на универсуме X. Формирование базы правил База правил — это множество правил, где каждому подзаключению сопоставлен определенный весовой коэффициент. База правил может иметь следующий вид (для примера используются правила различных конструкций): RULE_1: IF «Condition_1» THEN «Conclusion_1» (F1) AND «Conclusion_2» (F2); RULE_2: IF «Condition_2» AND «Condition_3» THEN «Conclusion_3» (F3); … RULE_n: IF «Condition_k» THEN «Conclusion_(q-1)» (Fq-1) AND «Conclusion_q» (Fq); Где Fi — весовые коэффициенты, означающие степень уверенности в истинности получаемого подзаключения (i = 1..q). По умолчанию весовой коэффициент принимается равным 1. Лингвистические переменные, присутствующие в условиях называются входными, а в заключениях выходными. Обозначения: n — число правил нечетких продукций (numberOfRules). m — кол-во входных переменных (numberOfInputVariables). s — кол-во выходных переменных (numberOfOutputVariables). k — общее число подусловий в базе правил (numberOfConditions). q — общее число подзаключений в базе правил (numberOfConclusions). Фаззификация входных переменных Этот этап часто называют приведением к нечеткости. На вход поступают сформированная база правил и массив входных данных А = {a1, ..., am}. В этом массиве содержатся значения всех входных переменных. Целью этого этапа является получение значений истинности для всех подусловий из базы правил. Это происходит так: для каждого из подусловий находится значение bi = μ(ai). Таким образом получается множество значений bi (i = 1..k). Реализация: private double[] fuzzification(double[] inputData) { int i = 0; double[] b = new double[numberOfConditions]; for (Rule rule : rules) { for (Condition condition : rule.getConditions()) { int j = condition.getVariable().getId(); FuzzySet term = condition.getTerm(); b[i] = term.getValue(inputData[j]); i++; } } return b; } Агрегирование подусловий Как уже упоминалось выше, условие правила может быть составным, т.е. включать подусловия, связанные между собой при помощи логической операции «AND». Целью этого этапа является определение степени истинности условий для каждого правила системы нечеткого вывода. Упрощенно говоря, для каждого условия находим минимальное значение истинности всех его подусловий. Формально это выглядит так: cj = min{bi}. Где: j = 1..n; i — число из множества номеров подусловий в которых участвует j-ая входная переменная. Реализация: private double[] aggregation(double[] b) { int i = 0; int j = 0; double[] c = new double[numberOfInputVariables]; for (Rule rule : rules) { double truthOfConditions = 1.0; for (Condition condition : rule.getConditions()) { truthOfConditions = Math.min(truthOfConditions, b[i]); i++; } c[j] = truthOfConditions; j++; } return c; } Активизация подзаключений На этом этапе происходит переход от условий к подзаключениям. Для каждого подзаключения находится степень истинности di = ci*Fi, где i = 1..q. Затем, опять же каждому i-му подзаключению, сопоставляется множество Di с новой функцией принадлежности. Её значение определяется как минимум из di и значения функции принадлежности терма из подзаключения. Этот метод называется min-активизацией, который формально записывается следующим образом: μ'i(x) = min {di, μi(x)}. Где: μ'i(x) — «активизированная» функция принадлежности; μi(x) — функция принадлежности терма; di — степень истинности i-го подзаключения. Итак, цель этого этапа — это получение совокупности «активизированных» нечетких множеств Di для каждого из подзаключений в базе правил (i = 1..q). Реализация: private List int i = 0; List double[] d = new double[numberOfConclusions]; for (Rule rule : rules) { for (Conclusion conclusion : rule.getConclusions()) { d[i] = c[i]*conclusion.getWeight(); ActivatedFuzzySet activatedFuzzySet = (ActivatedFuzzySet) conclusion.getTerm(); activatedFuzzySet.setTruthDegree(d[i]); activatedFuzzySets.add(activatedFuzzySet); i++; } } return activatedFuzzySets; } private double getActivatedValue(double x) { return Math.min(super.getValue(x), truthDegree); } Акумуляция заключений Целью этого этапа является получение нечеткого множества (или их объединения) для каждой из выходных переменных. Выполняется он следующим образом: i-ой выходной переменной сопоставляется объединение множеств Ei = ∪ Dj. Где j — номера подзаключений в которых участвует i-aя выходная переменная (i = 1..s). Объединением двух нечетких множеств является третье нечеткое множество со следующей функцией принадлежности: μ'i(x) = max {μ1(x), μ2(x)}, где μ1(x), μ2(x) — функции принадлежности объединяемых множеств. Реализация: private List List new ArrayList for (Rule rule : rules) { for (Conclusion conclusion : rule.getConclusions()) { int id = conclusion.getVariable().getId(); unionsOfFuzzySets.get(id).addFuzzySet(activatedFuzzySets.get(id)); } } return unionsOfFuzzySets; } private double getMaxValue(double x) { double result = 0.0; for (FuzzySet fuzzySet : fuzzySets) { result = Math.max(result, fuzzySet.getValue(x)); } return result; } Дефаззификация выходных переменных Цель дефаззификациии получить количественное значение (crisp value) для каждой из выходных лингвистических переменных. Формально, это происходит следующим образом. Рассматривается i-ая выходная переменная и относящееся к ней множество Ei (i = 1..s). Затем при помощи метода дефаззификации находится итоговое количественное значение выходной переменной. В данной реализации алгоритма используется метод центра тяжести, в котором значение i-ой выходной переменной рассчитывается по формуле: 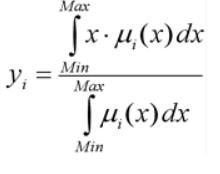 Рисунок 6. Формула дефаззификации Где: μi(x) — функция принадлежности соответствующего нечеткого множества Ei; Min и Max — границы универсума нечетких переменных; yi — результат дефаззификации. Реализация: private double[] defuzzification(List double[] y = new double[numberOfOutputVariables]; for(int i = 0; i < numberOfOutputVariables; i++) { double i1 = integral(unionsOfFuzzySets.get(i), true); double i2 = integral(unionsOfFuzzySets.get(i), false); y[i] = i1 / i2; } return y; } Пример: «Бронежилет IS легкий». Здесь «Бронежилет» — это лингвистическая переменная, а «легкий» её значение. Упрощенно говоря, правилом нечетких продукций (далее просто правилом) будем называть классическое правило вида «ЕСЛИ… ТО ...», где в качестве условий и заключений будут использоваться нечеткие высказывания. Записываются такие правила в следующем виде: IF (β1 IS α1) AND (β2 IS α2) THEN (β3 IS α3). Кроме «AND» также используются логическая связка «OR». Но такую запись обычно стараются избегать, разделяя такие правила на несколько более простых (без «OR»). Также каждое из нечетких высказываний в условии любого правила будем называть подусловием. Аналогично, каждое из высказываний в заключении называется подзаключением. Следующие примеры помогут зафиксировать определение: 1) IF (Бронежилет тяжелый) THEN (Солдат уставший); 2) IF (Муж трезвый) AND (Зарплата высокая) THEN (Жена довольная). |

