Асланян С.А._Математика_Зачет. Асланян С.А. Математика Зачет. Российский государственный социальный университет зачет по дисциплине Математика
 Скачать 60.8 Kb.
|
ЗАЧЕТ по дисциплине «Математика» Зачетная работа (тема практического задания)
Москва 2021 Теоретические вопросы Символы математической логики, их использование. Ответ: Для записи различных утверждений и логических операций над ними в современной математике часто используется аппарат символов, разработанный в математической логике. Выделяются 2 базисных (атомарных) типа высказываний. Во-первых, используется утверждение вида «объект Х есть элемент совокупности А определенных объектов». Этим утверждениям соответствует символ принадлежности. Приведенное высказывание записывается таким образом: Х с А (х принадлежит а) Во-вторых, используется высказывание вида: «совокупности объектов x и y совпадают, высказывания А и В совпадают». Таким высказыванием соответствует символ равенства (=). приведенные высказывания записывают в виде: А=В. Символ равенства используется тогда, когда 2 объекта или 2 совокупности объктов предс собой одно и то же, но определ по-разному, 2 выск-я явл одним и тем же но сформул разными словами. 25. Производные высших порядков. Ответ: Под производной высших порядков понимают дифференцирования функции более одного раза. Если производную 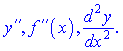 повторно дифференцировать, то получим производную второго порядка, или вторую производную функции  , и она обозначается Производная третьего порядка будет иметь вид 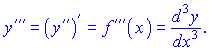 Аналогично получают формулы для нахождения производных высших порядков. При нахождении производной  порядке необходимо иметь производную  порядка. Исключение составляют функции для которых можно заметить тенденцию изменения производных. Это степенные, некоторые тригонометрические и экспоненциальные функции: В других случаях, для нахождения производных высших порядков от заданной функции нужно последовательно находить все ее производные низших порядков. Задачи 1. Даны вершины треугольника А (6;2), В (6;3), С (7;1). Составить уравнение высоты треугольника, проведенной из вершины A. Решение и ответ: 1. Найдем координаты вектора ВС: ВС (7-6; 1-3) = ВС (1; -2) 2. Уравнение прямой, перпендикулярной вектору с координатами (K, N) имеет вид: Kx + Ny + C = 0 В данном примере: 1 * х -2 * у + С = 0 3. Найдем С. Т.к. искомая прямая проходит через точку А(6;2), то подставив координаты точки в уравнение, найдем параметр С: 1 * 6 - 2 * 2 + С = 0 2 + С = 0 С = -2 4. Подставим значение С в уравнение прямой: 1 * х - 2 * у - 2 = 0 х - 2у -2 = 0 Выразим у через х: у = х/2 -1 - искомое уравнение 16. Найти градиент функции z = x2+2x+y2-3 Решение и ответ: Градиентом функции u = f(x,y,z) называется вектор, координатами которого являются частные производные данной функции, т.е.: Находим частные производные:    Тогда величина градиента равна:  Найдем градиент в точке А(0;0;0)  или  Модуль grad(u) - наибольшая скорость возрастания функции:  Направление вектора-градиента задаётся его направляющими косинусами:  25. Баскетболист забрасывает мяч в корзину с вероятностью 0,4 при одном броске. Найти вероятность того, что мяч попадёт в корзину 2 или 3 раза, если будет выполнено 5 бросков. Решение и ответ: вероятность попадания при 1 броске 0.4 вероятность промаха при 1 броске 0.6 было 5 бросков при 3 попаданиях P=0.6*0.6*0.4*0.4*0.4=0.024 при 2 попаданиях P=0.6*0.6*0.6*0.4*0.4=0.034 |
