шаблон ргр по прикладной механике. Российский химикотехнологический университет имени. Д. И. Менделеева
 Скачать 245.5 Kb. Скачать 245.5 Kb.
|
|
РОССИЙСКИЙ ХИМИКО-ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ имени. Д. И. МЕНДЕЛЕЕВА __________________________________________________________________ Кафедра инженерного проектирования технологического оборудования Расчетно – графическая работа № 3 Тонкостенные сосуды Вариант № Студент группы _____ ________________________________ (Ф.И.О.) Преподаватель доцент Щербак Н.Б. ________________ «___» ______________ 2020 г. Москва - 2020 г. Краткая теория расчета тонкостенных сосудовОкружные (тангенциальные) (σt) и меридиональные (σm) напряжения входят в уравнение Лапласа σt/ρt + σm/ρm = Р/s где ρt и ρm – радиусы кривизны в тангенциальном и меридиональном направлении, Р – избыточное давление в данной точке, s – толщина стенки сосуда. В этом уравнении два неизвестных σt и σm, поэтому дополнительно необходимо использовать второе уравнение равновесия отсеченной части сосуда в проекции на вертикальную ось (z), составленное по методу сечений ("РОЗУ"). Прочностной расчет Сложно напряженное состояние характеризуется тремя главными напряжениями σ1 ≥ σ2 ≥ σ3. По третьей гипотезе прочности σэкв = σ1 - σ3. Для тонкостенной оболочки σt, σm и σr взаимно перпендикулярны, σt и σm существенно больше σr, поэтому считаем σr ≈ 0 и, если σt > σm, то σ1 = σt, σ2 = σm, σ3 = σr ≈ 0. Условие прочности имеет вид: σэкв = σ1 - σ3 = σt – σr ≈ σt – 0 = σt [σ]. Вариант 1 (Заделка сверху) Дано: R1 = 2 м, R2 = 4 м, Н1 = 5 м, Н2 = 10 м, α=45°, β =60°, Плотность жидкости = 1 103 кг/м3, g=10 м/с2 [σ]= 100 МПа Определить σt, σm и Вариант А: PГ = 0.2 МПа, найти s Вариант B: s = 20 мм, найти PГ Решение: Тонкостенный сосуд разбивается на четыре расчетных участка. На каждом расчетном участке проводим сечение: 1-1 – конус (угол полураствора α) с газом (избыточное давление PГ) 2-2 – цилиндр (радиуса R1) с газом (PГ) 3-3 - цилиндр (радиуса R2) с жидкостью (плотность ρ) 4-4 – конус (угол полураствора β) с жидкостью I) Так как меридиональные напряжения (σm) во всех четырех сечениях действуют по прямым линиям – образующим конусов и цилиндров, а радиус кривизны прямой линии равен бесконечности ρm=∞, а при делении на ∞ получается ноль, тогда в уравнении Лапласа остается только одно неизвестное тангенциальное напряжение σt σt/ρt = Р/s → σt = ρt Р/s Поэтому сначала определим на всех четырех участках тангенциальное напряжение σt 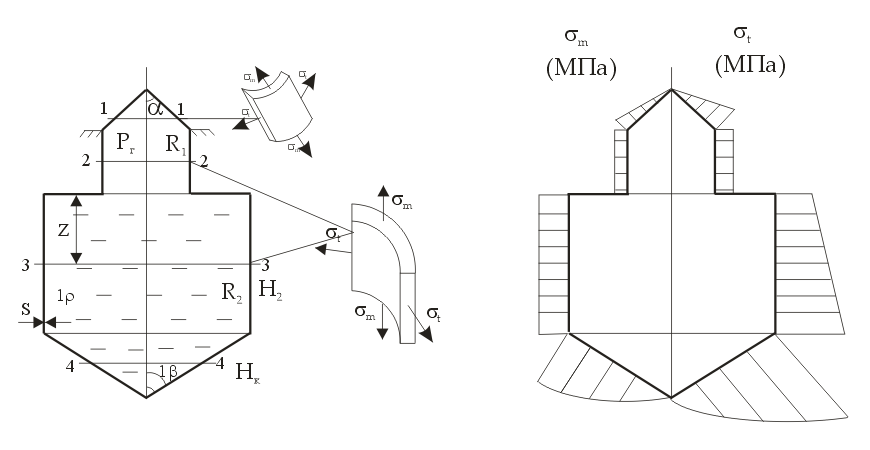 1. Сечение 1-1 – конус (угол полураствора α) с газом (PГ). Введем переменную r – радиус сечения (0 r R1). Избыточное давление P = Pг, радиус кривизны ρt = r/cosα 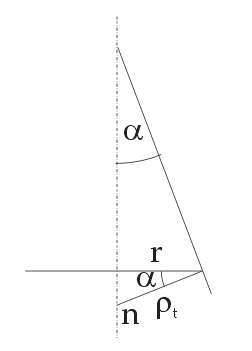 σt = ρt Р/s = rPг/[s cosα] σt = ρt Р/s = rPг/[s cosα]σt имеет линейную зависимость по r. Прямую проводим по двум точкам: при r=0 (вершина конуса) σt = 0, при r=R1 (основание конуса) σt = R1Pг/[s cosα] = 2 Pг/[s cos45°] = 2 1.4 Pг/s = 2.8Pг/s (МПа) 2. Сечение 2-2 – цилиндр (радиуса R1) с газом (PГ). Избыточное давление P = Pг, радиус кривизны ρt = R1 σt = ρt Р/s = R1 Pг/s = 2Pг/s (МПа) 3. Сечение 3-3 – цилиндр (радиуса R2) с жидкостью (плотность ρ) Введем переменную z – глубина погружения от верхнего уровня (0 z H2). Избыточное давление P = Pг + ρgz, радиус кривизны ρt = R2 σt = ρt Р/s = R2(Pг + ρgz)/s = 4(Pг + ρgz)/s σt имеет линейную зависимость по z. Прямую проводим по двум точкам: при z=0 (верхний уровень жидкости) σt = 4Pг/s (МПа), при z=H2 (основание цилиндра радиуса R2) σt = 4(Pг + ρgH2)/s МПа 4. Сечение 4-4 – конус (угол полураствора β) с жидкостью (плотность ρ) 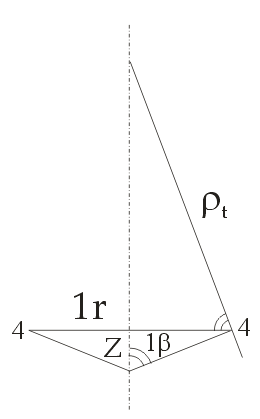 Введем переменную r – радиус сечения (0 r R2) и z (0 z Hк= R2 ctgβ = 4ctg60° = 2.31 м), где Hк – высота нижнего конуса, r = z tgβ. Избыточное давление P=Pг+ρgH2+ρg(Hк-z)=Pг+ρg(H2+Hк-z), радиус кривизны ρt = r/cosβ σt = ρt Р/s = r[Pг+ρg(H2+Hк-z)]/(s cosβ). Найдем значения σt в двух крайних точках: вершина конуса: r=0 → σt = 0, основание конуса: r=R2, z=Hк σt=R2(Pг+ρgH2)/(s cosβ)=4(Pг+ρgH2)/(s cos60°)=8(Pг+ρgH2)/s Подставим r = z tgβ → σt=z tgβ[Pг+ρg(H2+Hк-z)]/(s cosβ)=tgβ/(s cosβ){z[Pг+ρg(H2+Hк)]-ρgz2}. Исследуем функцию f(z) = z[Pг+ρg(H2+Hк)]-ρgz2 – парабола, ветви вниз, на максимум df/dz = РГ + ρg(H2+Hк) – 2gz df/dz(z0) = 0 → РГ + ρg(H2+Hк) – 2gz0 = 0 → z0 = РГ/(2ρg)+(H2+Hк)/2 = РГ/(2ρg)+(10+2.31)/2 > 6.155 м > Hк = 2.31 м т.е. экстремум лежит за пределами области изменения z → функция монотонно возрастает. II. Определим σm методом сечений ("РОЗУ"): 1) Разрезать 2) Отбросить часть, содержащую заделку 3) Заменить отброшенную часть силой давления Fд, направленную от отброшенной части 4) Уравновесить оставленную часть: ΣFz = 0 - сумма всех сил по вертикали равна нулю 1. Сечение 1-1 – конус (угол полураствора α) с газом (PГ). r – радиус сечения (0 r R1). Оставляем верхнюю часть конуса. 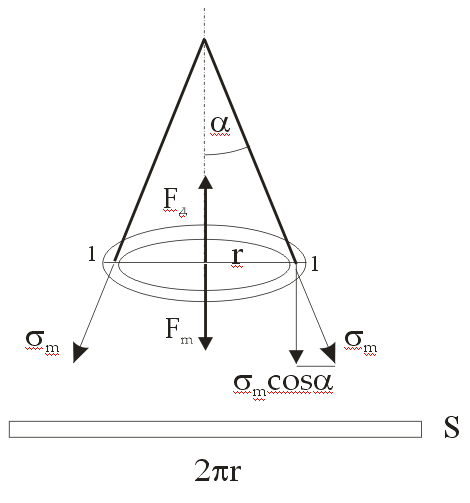 Избыточное давление P = Pг действует на круге радиуса r и дает силу давления Fд, направленную вверх Fд = Pг πr2 Меридиональное напряжение действует на кольце радиуса r и толщиной s по образующей и дает меридиональную силу Fm = σm 2πr s, вертикальная составляющая которой Fm cosα направлена вниз. Для равновесия Fд = Fm cosα Pг πr2 = σm 2πr s cosα → σm = r Pг /(2s cosα) σm имеет линейную зависимость по r. Прямую проводим по двум точкам: при r=0 (вершина конуса) σm= 0, при r=R1 (основание конуса) σm= R1Pг/[2s cosα] = 2Pг/[2s cos(45°)] = 1.4Pг/s (МПа) 2. Сечение 2-2 – цилиндр (радиуса R1) с газом (PГ). Отбрасываем верхнюю часть (с заделкой). 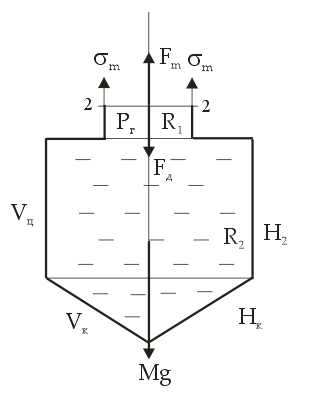 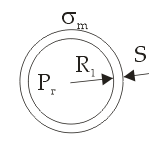 Избыточное давление P = Pг действует на круге радиуса R1 и дает силу давления Fд, направленную вниз Fд = Pг πR12 Меридиональное напряжение действует на кольце радиуса R1 и толщиной s вверх и дает меридиональную силу Fm = σm 2πR1 s, направленную вверх. Сила притяжения жидкости в цилиндре радиуса R2 и высотой Н2 и в конусе высотой Нк Мg = ρ(Vц + Vк)g = ρ(πR22H2 + πR22Hк/3)g = ρπR22(H2 + Hк/3)g Для равновесия Fm = Fд + Мg σm 2πR1 s = Pг πR12 + ρπR22(H2 + Hк/3)g → σm = R1[Pг + ρg(R2/R1)2(H2 + Hк/3)]/(2s) = 2[Pг + ρg(2)2(H2 + Hк/3)]/(2s) = [Pг + 4ρg(H2+Hк/3)]/s Сечение 3-3 – цилиндр с жидкостью на расстоянии z от верхнего уровня (глубина погружения) (0 z H2). Отбрасываем верхнюю часть (с заделкой). 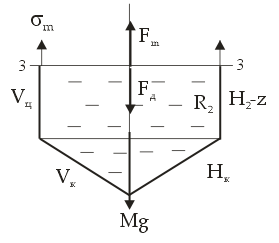 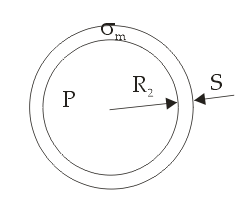 Избыточное давление P = Pг+ρgz действует на круге радиуса R2 и дает силу давления Fд, направленную вниз Fд = P πR22 Меридиональное напряжение действует на кольце радиуса R2 и толщиной s вверх и дает меридиональную силу Fm = σm 2πR2 s, направленную вверх. Сила притяжения жидкости в цилиндре радиуса R2 и высотой Н2-z и в конусе высотой Нк Мg = ρ(Vц + Vк)g = ρ[πR22 (H2–z) + πR22Hк/3]g = ρπR22(H2–z + Hк/3)g Для равновесия Fm = Fд + Мg σm 2πR2 s = (Pг+ρgz)πR22 + ρπR22(H2–z + Hк/3)g → σm = R2[Pг+ρg(H2+Hк/3)]/(2s) = 4[Pг+ρg(H2+Hк/3)]/(2s) = 2[Pг+ρg(H2 + Hк/3)]/s 4. Сечение 4-4 – конус (угол полураствора β) с жидкостью (плотность ρ) r – радиус сечения (0 r R2) и z (0 z Hк= 2.31 м), r = z tgβ. Отбрасываем верхнюю часть (с заделкой). Избыточное давление P=Pг+ρg(H2+Hк-z) действует на круге радиуса r и дает силу давления Fд, направленную вверх Fд = P πr2 = [Pг+ρg(H2+Hк-z)] πr2 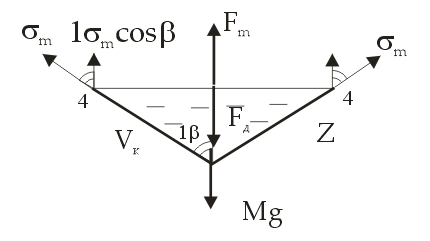 Меридиональное напряжение действует на кольце радиуса r и толщиной s по образующей и дает меридиональную силу Fm = σm 2πr s, вертикальная составляющая которой Fm cosβ направлена вверх. Сила притяжения жидкости в конусе высотой z Мg = ρVкg = ρ(πr2z/3)g Для равновесия Fm cosβ = Fд + Мg σm 2πr s cosβ = [Pг+ρg(H2+Hк-z)] πr2 + ρgπr2z/3 → σm = r[Pг+ρg(H2+Hк-2z/3)]/(2s cosβ) Найдем значения σm в двух крайних точках: вершина конуса: r=0 → σm = 0, основание конуса: r=R2, z=Hк σm=R2[Pг+ρg(H2+Hк/3)]/(2s cosβ)=4[Pг+ ρg(H2+Hк/3)]/s Подставим r = z tgβ → σm=z tgβ[Pг+ρg(H2+Hк-2z/3)]/(2s cosβ)=tgβ/(2s cosβ){z[Pг+ρg(H2+Hк)]-2ρgz2/3}. Исследуем функцию φ(z) = z[Pг+ρg(H2+Hк)]-2ρgz2/3 – парабола, ветви вниз, на максимум dφ/dz = РГ + ρg(H2+Hк) – 4gz/3 dφ/dz(z0) = 0 → РГ + ρg(H2+Hк) – 4gz0/3 = 0 → z0 = 3РГ/(4ρg)+3(H2+Hк)/4 = 3РГ/(4ρg)+3(10+2.31)/4 > 9.23 м > Hк = 2.31 м т.е. экстремум лежит за пределами области изменения z → функция монотонно возрастает. III. Определим искомый параметр из условия прочности max = tmax = R2(Pг+ρgH2)/(s cosβ) Вариант А, определим толщину стенки s s ≥ R2(Pг+ρgH2)/([σ] cosβ) = 4(2 105 + 1 103 10 10)/(100 106 0.5) = 24 10-3 м = 24 мм Вариант В, определим избыточное давление газа Pг Pг IV. Определим величины напряжений в МПа Вариант А 1. σt = 2.8Pг/s = 2.8 2 105/24 10-3 = 23.3 106 Па = 23.3 МПа, σm = σt/2 = 11.7 МПа 2. σt = 2Pг/s = 2 2 105/24 10-3 = 16.7 106 Па = 16.7 МПа, σm = [Pг + 4ρg(H2+Hк/3)]/s = [2 105 + 4 1 103 10(10+2.31/3)]/24 10-3 = 26.3 МПа 3. σt = 4Pг/s=33.3 МПа σt=4(Pг+ρgH2)/s=4(2 105+1 103 10 10)/24 10-3=50 106 Па=50 МПа σm=2[Pг+ρg(H2+Hк/3)]/s=2 [2 105+1 103 10(10+2.31/3)]/24 10-3=25.6 106 Па=25.6 МПа 4. σt = 8(Pг+ρgH2)/s = 100 МПа σm = 4[Pг+ρg(H2+Hк/3)]/s = 51.2 МПа Вариант В 1. σt = 2.8Pг/s = 2.8 1.5 105/20 10-3 = 21 106 Па = 21 МПа, σm = σt/2 = 10.5 МПа 2. σt = 2Pг/s = 2 1.5 105/20 10-3 = 15 106 Па = 15 МПа, σm = [Pг+4ρg(H2+Hк/3)]/s = [1.5 105+4 1 103 10(10+2.31/3)]/20 10-3 = 29 106 Па = 29 МПа 3. σt = 4Pг/s=30 МПа σt=4(Pг+ρgH2)/s=4(1.5 105+1 103 10 10)/20 10-3=50 106 Па=50 МПа σm=2[Pг+ρg(H2+Hк/3)]/s=2 [1.5 105+1 103 10(10+2.31/3)]/20 10-3=25.8 106 Па=25.8 МПа 4. σt = 8(Pг+ρgH2)/s = 100 МПа σm = 4[Pг+ρg(H2+Hк/3)]/s = 51.6 МПа Ответ: Вариант А s = 24 мм Вариант В Pг = 0.15 МПа Вариант 2 (Заделка в середине) 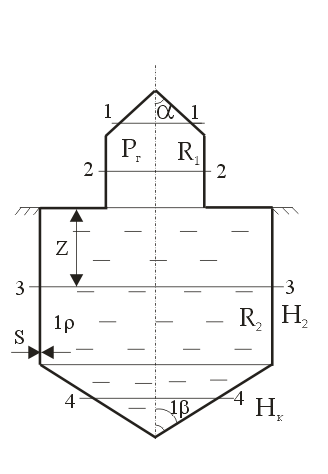  Отличие от варианта 1 будет заключаться в сечении 2 – 2 Избыточное давление P = Pг действует на круге радиуса R1 и дает силу давления Fд, направленную вверх Fд = Pг πR12 Меридиональное напряжение действует на кольце радиуса R1 и толщиной s вниз и дает меридиональную силу Fm = σm 2πR1 s, направленную вниз. Для равновесия Fm = Fд σm 2πR1 s = Pг πR12 → σm = R1Pг/(2s) Вариант 3 (Заделка снизу) 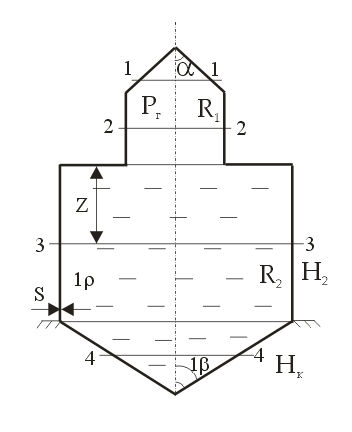 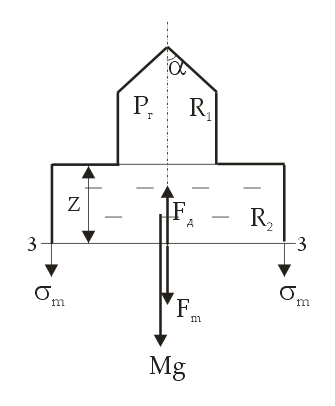 Отличие от варианта 2 будет заключаться в сечении 3 – 3 Избыточное давление P = Pг+ρgz действует на круге радиуса R2 и дает силу давления Fд, направленную вверх Fд = P πR22 Меридиональное напряжение действует на кольце радиуса R2 и толщиной s вверх и дает меридиональную силу Fm = σm 2πR2 s, направленную вниз. Сила притяжения жидкости в цилиндре радиуса R2 и высотой z Мg = ρVцg = ρπR22zg Для равновесия Fm + Мg = Fд σm 2πR2 s + ρπR22zg = (Pг+ρgz)πR22 → σm = R2Pг/(2s) |
