|
|
Курсовая работа. Нестабильные ядра. Радиоактивность.. Курсовая. Российской федерации федеральное государственное бюджетное
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Физический факультет
Нестабильные ядра. Радиоактивность.
Курсовая работа
Направление 14.03.02 Ядерная физика и технологии
Зав. Кафедрой д.ф-м.н., профессор Кадменский С.Г.
Обучающийся Щенов К.В.
Руководитель д.ф-м.н.,профессор Кадменский С.Г.
Воронеж 2021
Содержание
Введение 3-4
Основные причины неустойчивости ядер 5-8
Общие законы радиоактивного распада 9-13
Статистический характер радиоактивного распада 14-16
Вывод 17
Литература 18
Введение.
Атомное ядро является связанной системой, состоящей из Z протонов и N нейтронов, A = (N + Z) – массовое число.
В настоящее время известно 3500 атомных ядер. В зависимости от соотношения между числом нейтронов N и числом протонов Z в ядре атомные ядра делятся на две группы: стабильные ядра и радиоактивные ядра. Число стабильных ядер всего
300. На рис. 1 показана N-Z-диаграмма атомных ядер. Стабильные атомные ядра показаны черным цветом.
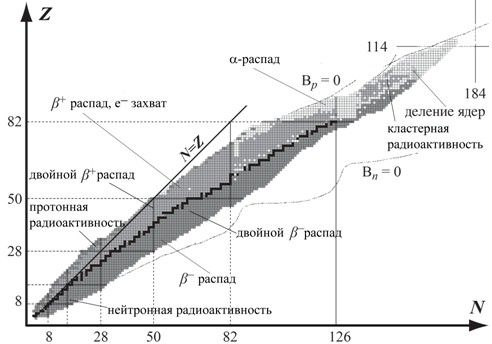
Рис.1.1
В области легких стабильных ядер число протонов примерно равно числу нейтронов. В тяжелых стабильных ядрах число нейтронов в 1.5–2.0 раза превышает число протонов.
Первые же представления о радиоактивности появились раньше, чем были открыты сами атомные ядра (1911 г.). Антуан Анри Беккерель в 1896 году, неожиданно обнаружил неизвестное ранее излучение, которое испускали соли урана. Тогда это излучение связывали с атомными процессами. Лишь с открытием атомных ядер стало ясно, что это внутриядерный процесс. Изучая ионизующую способность различных минералов, супруги Пьер и Мария Кюри обнаружили радиоактивность тория, полония и радия (1898 г.). К концу 1904 г., благодаря работам Э. Резерфорда и Ф. Содди, было обнаружено около 40 элементов, обладающих радиоактивными свойствами. Так было открыто явление радиоактивности – способности некоторых химических элементов самопроизвольно распадаться, превращаясь в другие химические элементы. Подавляющее число атомных ядер, известных на данный момент, является радиоактивными (≈ 3000).
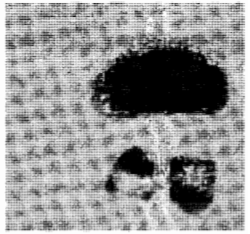
Рис. 1.2
Первое свидетельство радиоактивного распада атомных ядер, обнаруженное Беккерелем.
На фотопластинке отчётливо видны потемнения, образовавшиеся в результате, что Беккерель положил на нее образцы урановой соли.
Основные причины неустойчивости ядер.
Как отмечалось ранее, большинство ядер является радиоактивными изотопами. На характеристики их радиоактивного распада оказывают существенное влияние взаимодействия, вызывающие распад: сильные (альфа-распад), слабые (бета-распад) и электромагнитные (гамма-распад). Но каков бы ни был вид радиоактивного распада, причиной является большая масса первоначального ядра, чем сумма масс конечного ядра и испускаемых частиц, то есть его энергетическая выгодность. Это означает, что необходимым (но недостаточным, ввиду запрета другими законами сохранения) условием является неравенство:
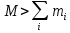
(1)
Где: M – масса исходного ядра, 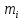 – массы продуктов распада; – массы продуктов распада;
Радиоактивный распад характеризуется временем его протекания (временем жизни), типом испускаемых частиц (так же их энергиями), а при вылете из ядра нескольких частиц, ещё и относительными углами между направлениями их вылета. Так же иногда изучается ориентация спинов конечных ядер и вылетающих частиц.
Основные типы распадов в природе по сорту испускаемых частиц:
Альфа-распад (испускание ядрами α-частиц).
Явление α-распада состоит в том, что тяжёлые ядра ( Z > 60 ) самопроизвольно испускают ядро 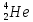 , при этом массовое число ядра уменьшается на четыре единицы, а атомный номер на две: , при этом массовое число ядра уменьшается на четыре единицы, а атомный номер на две:
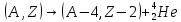
Для того что бы альфа-распад произошел, необходимо выполнения неравенства (1):
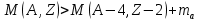
Причем энергия:
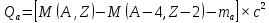
Откуда видно, что основная энергия будет уноситься именно α –частицей, так как 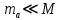 . .
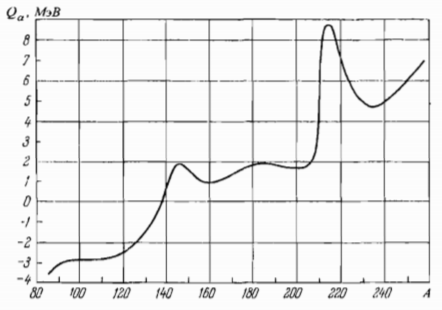 График экспериментальной зависимости энергии α – распада от массового числа А (рис 2.1): График экспериментальной зависимости энергии α – распада от массового числа А (рис 2.1):
Рис. 2.1
Бета-распад (испускание или поглощение электрона и антинейтрино или позитрона и нейтрино).
При β-распаде в ядре происходит превращение нейтрона в протон или наоборот с одновременным самопроизвольным испусканием лептонов 1-го поколения: электрона (или соответственно позитрона) и электронное нейтрино (или антинейтрино). При этом переход осуществляется в ядро с тем же массовым числом А, но с атомным номером Z, на единицу большим или меньшим.
Существует три основных типа β-распада со схемами:
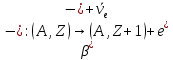
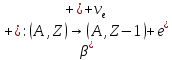
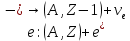
Β-распад – процесс не внутриядерный, а внутринуклонный, ввиду слабых взаимодействий. В отличии от альфа-распада β-радиоактивные ядра имеются во всей области значений массового числа А. Это сложное явление, связанное как с физикой слабых взаимодействий, так и со структурой ядра.
Бета-распад, полагая массу нейтрино и антинейтрино равными нулю, разрешен при следующих соотношениях (превращениях внутри ядра):
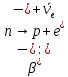 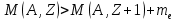
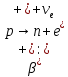 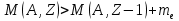
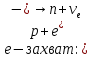 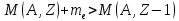
При е-захвате ядро поглощает один из электронов атомной оболочки (в основном из самой ближайшей К-оболочки), испуская нейтрино.
Гамма-распад.
Явление γ-излучения ядер состоит в том, что ядро (A,Z) испускает γ-квант (жесткое электромагнитное излучение) без изменения массового числа А и заряда ядра Z. Испускание γ-излучения обычно происходит после α- или β-распадов атомных ядер, если образовавшееся ядро образуется в возбужденном состоянии.
Гамма-излучение возникает при распаде возбужденных состояний ядер. Спектр γ-излучения всегда дискретен из-за дискретности ядерных уровней. С точностью до незначительной энергии отдачи ядра энергия γ-перехода равна разности энергий уровней, между которыми происходит γ-переход.
Гамма-излучение ядер обусловлено взаимодействием нуклонов ядра с электромагнитным полем. В отличие от β-распада, γ-излучение − явление не внутринуклонное, а внутриядерное. Изолированный свободный нуклон испустить или поглотить γ-квант не может из-за совместного действия законов сохранения энергии и импульса. В то же время внутри ядра нуклон может испустить γ-квант, передав при этом часть импульса другим нуклонам.
Времена жизни γ-радиоактивных ядер обычно изменяются от 10 -8 с до 10-17 с, т. е. в среднем они значительно меньше времен жизни по отношению к α- и β-распадам. Причина в том, что интенсивность электромагнитных взаимодействий всего лишь на три порядка слабее ядерных. Время жизни γ-радиоактивных ядер зависит от различия спинов и четностей начального и конечного состояний, между которыми происходит γ-переход.
Так же в природе встречаются спонтанное деление (распад ядра на два осколка сравнимой массы), кластерная радиоактивность, двойные бета-распады (как 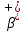 , так и , так и 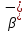 , протонная радиоактивность и (практически невозможная) нейтронная радиоактивность. , протонная радиоактивность и (практически невозможная) нейтронная радиоактивность.
Каждое радиоактивное ядро путём бомбардировки стабильных ядер частицами. С этой точки зрения, радиоактивность можно рассматривать, как распад составного ядра. Причём физической границы между радиоактивностью и распадом составного ядра нет. Несмотря на это, радиоактивность выделяется в самостоятельный раздел ядерной физики. Граница между этими процессами определяется, а возможностями измерительной аппаратуры. На практике к радиоактивным относят ядра, времена жизни которых могут быть измерены радиотехническими методами. Причём именно физическая область времён жизни их охватывает промежутки от сколь угодно больших, до превышающих характерное ядерное время пролёта.
Общие законы радиоактивного распада.
Постоянная распада.
Период полураспада и среднее время жизни.
Вековое равновесие.
Процесс радиоактивного распада – явление принципиально статистическое (случайное). Для описания протекания таких событий используют их вероятности. Атомные ядра даже одного сорта распадаются за разное время. Введена такая величина как среднее время жизни τ. Благодаря наблюдению огромного числа распадов, выяснили, что τ не зависит от способа получения этих ядер или частиц, а также от внешних условий (температура, давление, агрегатное состояние). Поэтому данная величина является физической характеристикой скорости распада, а обратная к ней величина λ называемая постоянной распада, имеет физический смысл вероятности распада в единицу времени.
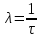
Если взять большое число N одинаковых нестабильных ядер, то за единицу времени в среднем будет распадаться λ×N ядер. Величина λN называется активностью. Она характеризует интенсивность излучения, причём не отдельных ядер, а препарата в целом.
Существенное свойство постоянной распада выражается в независимости от времени, так как различные моменты времени никак не выделены с точки зрения вероятности распада, зависит лишь от времени жизни ядра. По аналогии: если бы люди не старели, а гибли лишь в несчастных случаях.
Теперь можно сформулировать основной закон радиоактивного распада, показывающий, как со временем в среднем меняется число радиоактивных ядер в образце или нестабильных частиц в пучке.
Если в момент времени t имеется большое число N радиоактивных ядер (частиц), то за промежуток времени dt распадется в среднем dN ядер. В соответствии с определением величины λ получим:
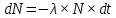
Знак минус означает уменьшение общего количества ядер (частиц). Затем нужно проинтегрировать данное соотношение. В результате получим искомый закон:
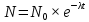 (2) (2)
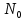 – количество ядер в выбранный произвольно начальный момент t. – количество ядер в выбранный произвольно начальный момент t.
Отмечается, что закон относится к статистически средним и справедлив лишь для существенно большого количества ядер (частиц).
Теперь можно определить ещё одну, выше введённую величину активности (интенсивности) излучения:
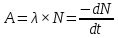
Активность так же уменьшается со временем по экспоненциальному закону. Единицей измерения её принято считать либо беккерель (1Бк = 1 распад в секунду), либо кюри (1Ки = 3,7×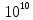 Бк). Бк).
Через постоянную распада λ выражается ещё одна величина, характеризующая интенсивность процесса радиоактивности – период полураспада 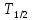 . Периодом полураспада называется время, за которое число радиоактивных ядер уменьшится в два раза. . Периодом полураспада называется время, за которое число радиоактивных ядер уменьшится в два раза.
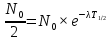
Откуда выразим:
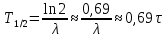
Для определения периода полураспада или же постоянной распада, рядом с препаратом можно поставить счётчик. Число отсчётов за равные промежутки времени которого пропорциональны λN. Далее строится график логарифма активности от времени. График может иметь разную форму, в зависимости от того, с какими распадами мы имеем дело. Для примера рассмотрим одиночный распад:
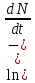
График такого распада должен иметь вид прямой, которая проводится по методу наименьших квадратов (с наименьшим среднеквадратичным отклонением полученных точек от прямой), так как мы имеем отношение со средними величинами. Тангенс этой прямой и будет равен постоянной распада λ.
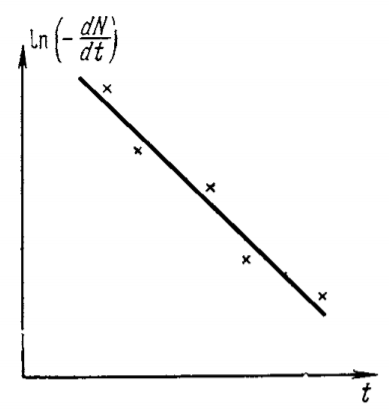
рис. 3.1
Сложный распад может случиться из-за содержания в препарате нескольких разных сортов ядер или, например, в случае, который рассмотрим ниже – при последовательном распаде одного и того же ядра. Это ситуация, когда после распада первого ядра образовавшееся ядро само оказывается радиоактивным, так что происходит последовательный распад исходного ядра: 1-2-3.
Изменение числа ядер в это случае определяется системой, смысл которой в том, что количество исходных ядер убывает, количество вторых ядер убывает за счёт их собственного распада, но пополняется за счёт распада первых:
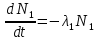
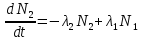
Введём начальные условия: 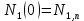 , , 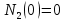
Тогда система примет вид: 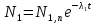 , , 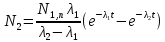
Далее рассмотрим два случая:
А) 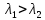 – первый распад короткоживущий, второй – долгоживущий. – первый распад короткоживущий, второй – долгоживущий.
Тогда суммарная активность будет монотонно уменьшаться (коэффициенты при обеих экспонентах имеют одинаковые знаки). (Рис.3.2)
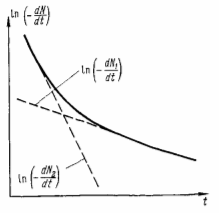 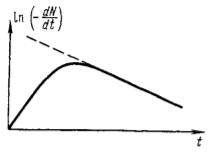
Рис.3.2
Рис. 3.3
Б) 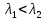 – первый распад долгоживущий, второй – короткоживущий. То вначале происходит рост суммарной активности за счёт накопления вторых ядер. Далее, при больших временах, вклад второй экспоненты становится довольно мал и активности ядер практически сравняются (Рис.3.3). Наступает радиоактивное равновесие: – первый распад долгоживущий, второй – короткоживущий. То вначале происходит рост суммарной активности за счёт накопления вторых ядер. Далее, при больших временах, вклад второй экспоненты становится довольно мал и активности ядер практически сравняются (Рис.3.3). Наступает радиоактивное равновесие:
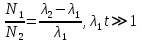
Предельным случаем радиоактивного равновесия является вековое равновесие. Оно устанавливается в случает нескольких n последовательных распадов с периодом полураспада исходных ядер намного превосходящим остальных: 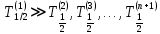
Примером может послужить цепочка из 14 последовательных распадов превращения изотопа урана 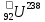 в изотоп свинца в изотоп свинца 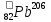 . Период полураспада первого равен . Период полураспада первого равен 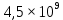 лет, а промежуточных ядер-продуктов варьируется долей секунды до сотен тысяч лет. лет, а промежуточных ядер-продуктов варьируется долей секунды до сотен тысяч лет.
При вековом равновесии, например, двух последовательных распадов  можно пренебречь, что приведёт к простому соотношению: можно пренебречь, что приведёт к простому соотношению:
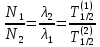
Так же и для большего числа последовательных распадов после установления векового равновесия количество ядер каждого изотопа будет пропорционально периоду полураспада этого изотопа:
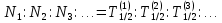
Как мы знаем, распад ядра может происходить как из основного (самого низкого по энергии состояния), так и из высоких (возбуждённых) состояний. В соответствии с принципом неопределённости Гейзенберга, энергия распадающийся системы не может быть определена точно. Всякое распадающееся состояние со средним временем жизни τ, описывается волновой функцией ψ(t), квадрат модуля которой убывает со временем по тому же экспоненциальному закону радиоактивного распада, как и в (2).
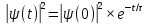
Вследствие неопределённости, о радиоактивном распаде говорят, как о статистическом процессе.
Статистический характер радиоактивного распада.
Радиоактивный распад является статистическим процессом. То есть конкретное радиоактивное ядро может распасться в любой момент времени, а закономерности процесса будут наблюдаться только в случае распада достаточно большого количества ядер.
Пусть N – общее количество ядер определённого вида, n – количество распавшихся ядер за время t, а 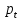 – вероятность распада отдельного ядра за это время. Тогда вероятность распада n ядер за время t будет распределяться по биномиальному закону и будет равно: – вероятность распада отдельного ядра за это время. Тогда вероятность распада n ядер за время t будет распределяться по биномиальному закону и будет равно:
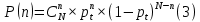
Причем 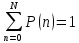 . .
Основными характеристиками случайной величины являются математическое ожидание M и дисперсия D. Для биномиального распределения имеем:
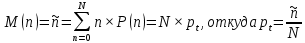
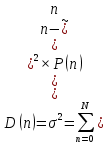
Биномиальное распределение применяется лишь при скудной статистике. В других случаях применяется распределение Пуассона.
Условиями перехода биномиального распределения в распределение Пуассона являются: 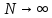 , , 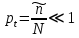 . .
Тогда уравнение (3) при 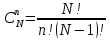 переходит в: переходит в:
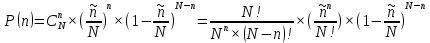
Соблюдая условия перехода, определим предельные значения членов уравнения:
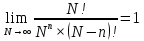
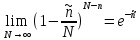
Получим финальный вид распределения Пуассона:
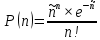
При таком распределении абсолютная флуктуация наблюдаемого числа распадов будет: 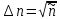
Это означается, что фактическое число распадов за заданное время в большей части будет отличаться от среднего не более, чем на 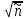 . .
Например: для препарата за 1 мсек с радиоактивностью 1 мкюри 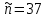 . Фактическое число распадов для данного случая лежит в интервале . Фактическое число распадов для данного случая лежит в интервале 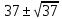 . Поэтому однократное измерение его радиоактивности в течение 1 мсек даст точность . Поэтому однократное измерение его радиоактивности в течение 1 мсек даст точность 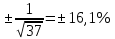 . При измерении этого же препарата в течение 1 сек, . При измерении этого же препарата в течение 1 сек, 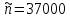 , , 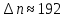 , следовательно точность величины радиоактивности возрастёт до , следовательно точность величины радиоактивности возрастёт до 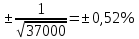 . .
Получается, что, вследствие статистического характера закона радиоактивного распада точность всяких измерений радиоактивности улучшается с увеличением числа зарегистрированных актов распада, и зачастую именно требование определённой точности результатов задаёт необходимую длительность измерений.
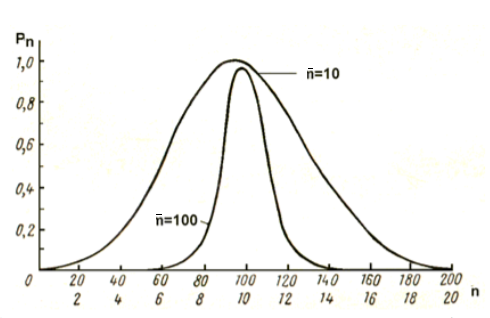
Рис. 4.1
Относительные вероятности чисел актов распада 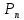 в единицу времени при двух различных средних числах распада. в единицу времени при двух различных средних числах распада.
Подытожим: законы радиоактивного распада носят статистический характер. Они верны лишь в тех случаях, когда числа атомов, распадающихся за единицу времени, достаточно велики, так что можно пренебречь относительно незначительными отклонениями от средних значений рассматриваемых статистических величин. Но при малых скоростях распада статистические отклонения от среднего могут сыграть существенную роль.
Статистические отклонения при радиоактивном распаде подчиняются определённым закономерностям:
- Вероятность появления малых отклонений больше вероятности больших отклонений от среднего, иначе говоря, вероятность 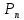 появления статистических отклонений есть убывающая функция их величины. появления статистических отклонений есть убывающая функция их величины.
- Вероятность появления случайных отклонений не зависит от их знака, т.е. статистические отклонения, равные по абсолютной величине, но противоположные по знаку, встречаются одинаково часто. Значение истинной скорости распада может быть получено лишь как среднее при достаточно большой продолжительности наблюдений (если, конечно, можно пренебречь уменьшением количества радиоактивного изотопа за выбранное время). Различия в скоростях распада за равные промежутки времени при постоянной средней скорости распада называются радиоактивными флуктуациями.
Вывод.
Открытие радиоактивности оказало огромное влияние на развитие науки и техники. Оно ознаменовало начало эпохи интенсивного изучения свойств и структуры вещества. Новые перспективы, возникшие в энергетике, промышленности и многих других областях человеческой деятельности благодаря овладению ядерной энергией, были вызваны к жизни обнаружением способности химических элементов к самопроизвольным превращениям. За работы, связанные с исследованием и применением радиоактивности, было присуждено более 10 Нобелевских премий по физике и химии.
Например, в настоящее время, благодаря открытию сверхтяжёлых ядер, прогнозируется существование ещё одного острова стабильности в Z = 110-114 и N = 178-184 на N-Z диаграмме (Рис 1.1). Но трудность проникновения на остров стабильности связана с тем, что нет комбинации соответствующих ядер, использование которых в качестве мишени и налетающей частицы позволили бы попасть в центр острова стабильности. Достаточно хорошее согласие теоретических расчетов с полученными в последнее время экспериментальными данными, говорят о перспективности нахождения и подтверждения существования долины стабильности.
Так же получение и использование пучков радиоактивных ядер используется, как один из эффективных методов изучения экзотических ядер.
Список литературы.
1. Ю. М. Широков, Н. П. Юдин. Ядерная физика. М.: Наука, 1980.
2. Б. С. Ишханов, И. М. Капитонов, Н.П. Юдин. «Частицы и атомные ядра». Москва, 2007.
3. К. Н. Мухин, Экспериментальная ядерная физика, -М., Энергоатомиздат, 1993.
4. Физические основы радиохимии. В.П. Медведев, А.В. Очкин, М.А. Семенов; Под редакцией А.В. Очкина. – М.: Изд-во НИЯУ МИФИ, 2011.
5. Б.С. Ишханов, Э. И. Кэбин. Экзотические ядра. М.: Изд. Московского университета, 2002.
6. Б. С. Ишханов, Радиоактивность.
7. Методическое описание Т. А. Тулиной, «Радиоактивность. Вводная лекция для студентов». (https://nuclab.spbu.ru/old/common/)
|
|
|
 Скачать 302.43 Kb.
Скачать 302.43 Kb.


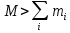
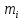 – массы продуктов распада;
– массы продуктов распада;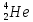 , при этом массовое число ядра уменьшается на четыре единицы, а атомный номер на две:
, при этом массовое число ядра уменьшается на четыре единицы, а атомный номер на две: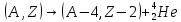
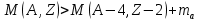
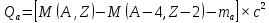
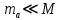 .
.
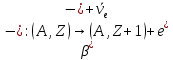
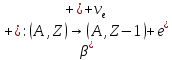
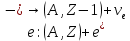
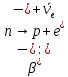
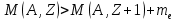
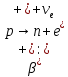
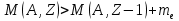
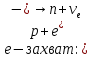
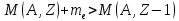
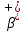 , так и
, так и 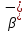 , протонная радиоактивность и (практически невозможная) нейтронная радиоактивность.
, протонная радиоактивность и (практически невозможная) нейтронная радиоактивность.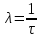
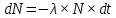
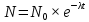 (2)
(2)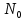 – количество ядер в выбранный произвольно начальный момент t.
– количество ядер в выбранный произвольно начальный момент t. 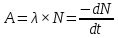
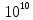 Бк).
Бк).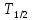 .
. 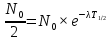
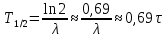
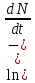

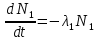
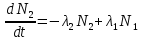
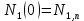 ,
, 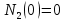
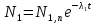 ,
, 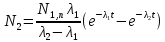
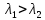 – первый распад короткоживущий, второй – долгоживущий.
– первый распад короткоживущий, второй – долгоживущий.

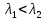 – первый распад долгоживущий, второй – короткоживущий. То вначале происходит рост суммарной активности за счёт накопления вторых ядер. Далее, при больших временах, вклад второй экспоненты становится довольно мал и активности ядер практически сравняются (Рис.3.3). Наступает радиоактивное равновесие:
– первый распад долгоживущий, второй – короткоживущий. То вначале происходит рост суммарной активности за счёт накопления вторых ядер. Далее, при больших временах, вклад второй экспоненты становится довольно мал и активности ядер практически сравняются (Рис.3.3). Наступает радиоактивное равновесие: 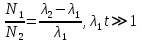
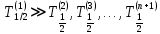
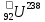 в изотоп свинца
в изотоп свинца 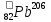 . Период полураспада первого равен
. Период полураспада первого равен 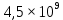 лет, а промежуточных ядер-продуктов варьируется долей секунды до сотен тысяч лет.
лет, а промежуточных ядер-продуктов варьируется долей секунды до сотен тысяч лет.  можно пренебречь, что приведёт к простому соотношению:
можно пренебречь, что приведёт к простому соотношению: 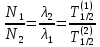
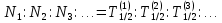
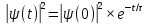
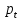 – вероятность распада отдельного ядра за это время. Тогда вероятность распада n ядер за время t будет распределяться по биномиальному закону и будет равно:
– вероятность распада отдельного ядра за это время. Тогда вероятность распада n ядер за время t будет распределяться по биномиальному закону и будет равно: 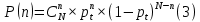
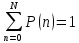 .
.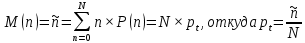
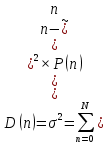
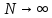 ,
, 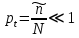 .
. 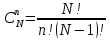 переходит в:
переходит в: 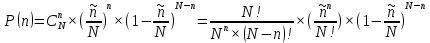
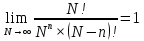
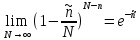
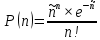
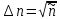
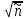 .
. 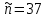 . Фактическое число распадов для данного случая лежит в интервале
. Фактическое число распадов для данного случая лежит в интервале 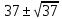 . Поэтому однократное измерение его радиоактивности в течение 1 мсек даст точность
. Поэтому однократное измерение его радиоактивности в течение 1 мсек даст точность 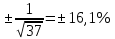 . При измерении этого же препарата в течение 1 сек,
. При измерении этого же препарата в течение 1 сек, 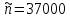 ,
, 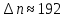 , следовательно точность величины радиоактивности возрастёт до
, следовательно точность величины радиоактивности возрастёт до 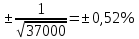 .
.
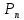 в единицу времени при двух различных средних числах распада.
в единицу времени при двух различных средних числах распада.