Вискозиметр. Вискозиметр DV3T. Ротационный вискозиметр Brookfield dv3t общее описание
 Скачать 331.94 Kb. Скачать 331.94 Kb.
|
Обработка результатов измерений динамической вязкости с помощью программы Rheocalc V3.2Для получения исходных данных в качестве реологического объекта была исследована система, представляющая собой концентрированный мицеллярный раствор анионактивных и неионогенных поверхностно-активных веществ (ПАВ), используемый в качестве средства для мытья посуды и реализуемый под товарным названием «Dish Drops». Для проведения измерений был выбран UL- адаптер, предназначенный для измерения динамической вязкости образцов с вязкостью менее 2000 мПа·с. При этом для получения результатов с допустимой ошибкой необходимо, чтобы минимальная вязкость образцов превышала значение 3,2 мПа·с и процент закручивания калиброванной пружины был не менее 10 %. Для этого в ячейку UL-адаптера помещали 16 см3 мицеллярного раствора ПАВ, ячейку с погруженным шпинделем термостатировали при температуре 30 °С и определяли динамическую вязкость при постепенно увеличиваемой скорости сдвига и затем при ее уменьшении. Скорость сдвига регулировали путем задания набора скоростей вращения с помощью программы Rheocalc V 3.2 (внешнее управление). На рис. 6 представлен график зависимости динамической вязкости (мПа·с) от скорости сдвига (1/с) для исследуемого объекта, получаемый автоматически с помощью программы Rheocalc V 3.2. 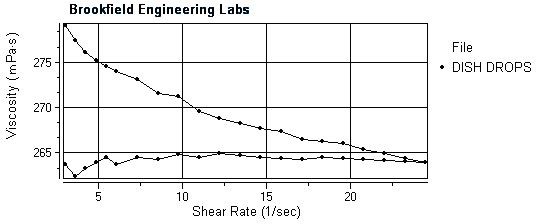 Рисунок 6 – Изменение динамической вязкости в зависимости от скорости сдвига для мицеллярного раствора ПАВ В процессе построения графика было установлено, что динамическая вязкость системы понижается с повышением скорости сдвига, а при последующем ее понижении практически не изменяется. Таким образом, данная система изменяет свои свойства с продолжительностью сдвиговой деформации (происхо-дит понижение динамической вязкости). Следовательно, систему можно отнести к тиксотропному типу поведения. Среди моделей, предлагаемых программой Rheocalc V3.2, для описания таких систем могут быть использованы только обобщенные модели неньютоновских жидкостей и тел (степенной закон и закон Хершель – Балклей). При расчете этих моделей было установлено, что предельное напряжение сдвига, определяемое по модели Хершель – Балклей незначительно, а следовательно, система ведет себя как неньютоновская жидкость (способна течь при любых напряжениях сдвига). В таком случае целесообразно описать полученные экспериментальные данные с помощью степенного закона. Программа рассчитывает постоянные модели и представляет график зависимости напряжения сдвига (Н/м2) от скорости сдвига (1/с) экспериментальных (Raw Data) и расчетных (Fitted Curve) данных (рис. 7). На графике также представлены расчетные значения индекса консистенции (Consistency Index), индекс течения (Flow Index) и коэффициент сходимости экспериментальных и расчетных данных (CoF). Значение индекса течения, близкого к единице, свидетельствует о том, что реологическое поведение системы (при данной температуре) близко к ньютоновскому, и тиксотропные свойства проявляются только в небольшой степени (понижение динамической вязкости в процессе измерения составило всего 5 %). 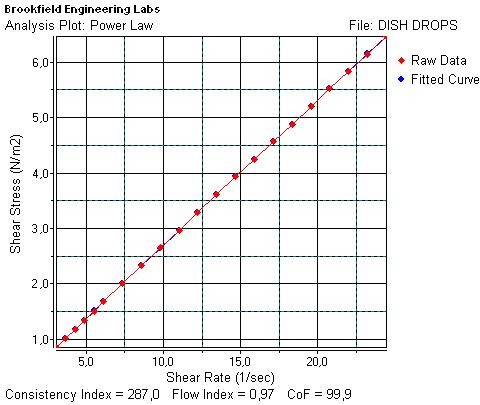 Рисунок 7 – Результат обработки экспериментальных данных программой Rheocalc V 3.2 с применением степенного закона В табл. 1 представлены коды измерительных шпинделей и диапазоны вязкости. Таблица 1 - Коды измерительных шпинделей и диапазоны вязкости
|
