Курсова. Розрахунки й оптимізація характеристик
 Скачать 0.54 Mb. Скачать 0.54 Mb.
|
|
Так як в каналі зв’язку не використовується завадостійке кодування, то припустима імовірність помилки символу на виході демодулятора дорівнює значенню 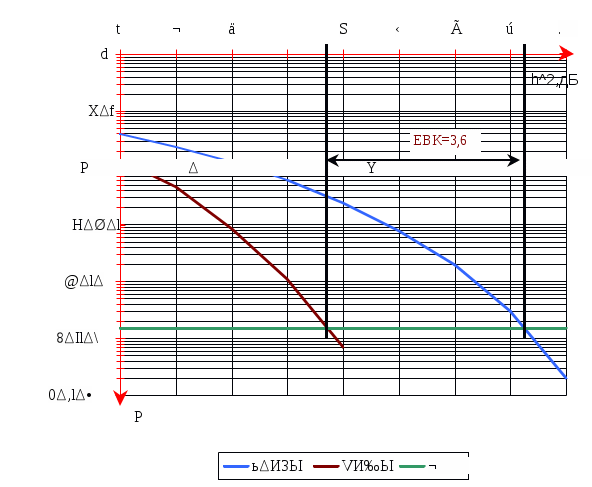 Рис.5 – Завадостійкість систем передачі без завадостійкого кодування та з ним. З графіка визначаємо Розрахуємо необхідне відношення сигнал-шум на вході демодулятора 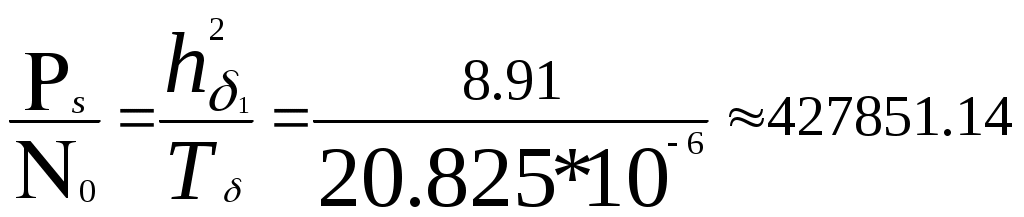 5. Вибір коректуючого коду та розрахунок завадостійкості систем зв’язку з кодуванням. Коректуючи коди дозволяють підвищити завадостійкість і завдяки цьому зменшити необхідне відношення сигнал-шум на вході демодулятора для заданої ймовірності помилки прийнятих сигналів. Величина, що показує в скільки разів (на скільки децибел) зменшується необхідне відношення сигнал-шум на вході демодулятора завдяки використанню кодування, називається енергетичним виграшем кодування (ЕВК). Широке розповсюдження дістали циклічні коди Боуза-Чоудхурі-Хоквінгема (БЧХ). За параметрами вони близькі до досконалих кодів і разом з тим вимагають відносно простих схем кодерів та декодерів. У кодів БЧХ основні параметри пов’язані співвідношеннями : де k- число інформаційних символів, а m- найменше ціле, за якого задовольняється співвідношення Вибираючи коректуючий код, я зупинився на кодові з довжиною n=108 та кратністю помилок що виправляються Якщо в каналі зв’язку без кодування для забезпечення заданої ймовірності помилки необхідне відношення сигнал-шум 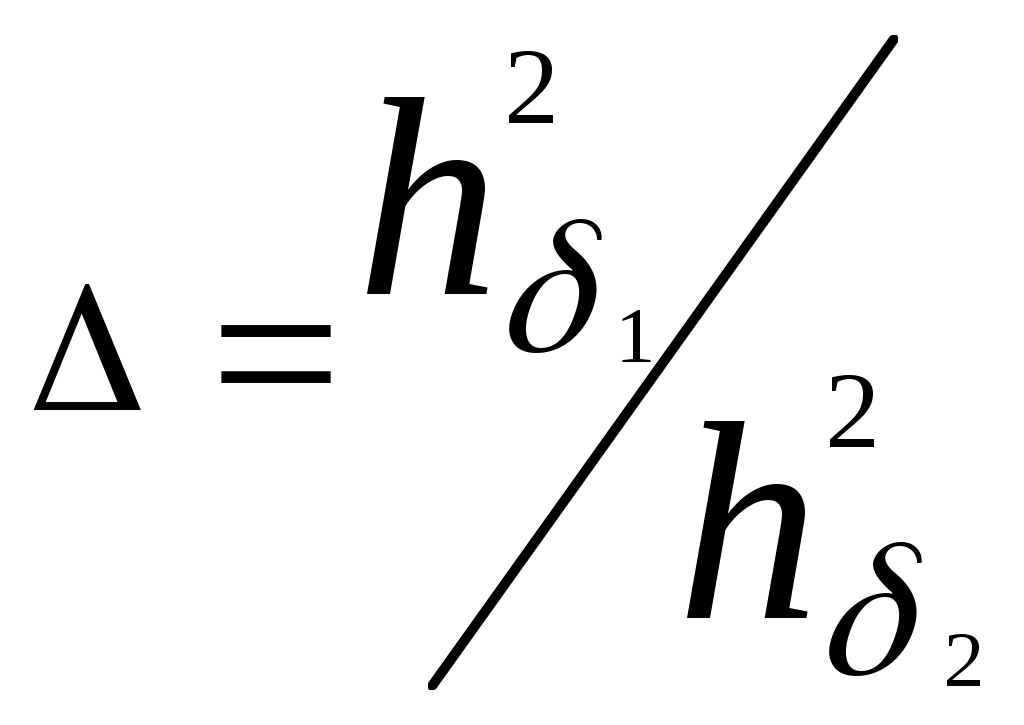 або або Під декодування з виправленням помилок імовірність помилкового декодування кодових комбінацій 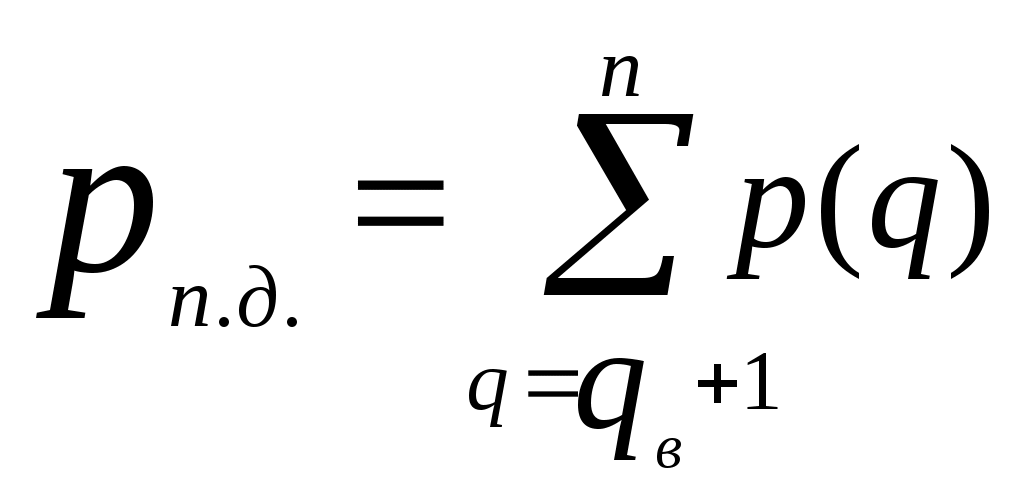 , (5.4) , (5.4)де імовірність помилки кратності q; (5.6) число сполучень із n по q; р- імовірність помилки двійкового символу на вході декодера, розрахунок якої для гауссового каналу зв’язку з постійними параметрами розглянутий у розділі 4. Для переходу від імовірності Оскільки при помилковому декодуванні кодової комбінації 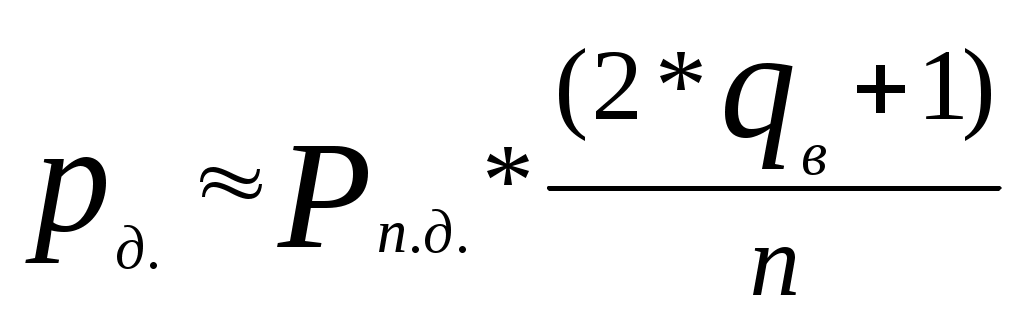 . .Розрахувавши імовірність помилки заносимо результати в таблицю2 та на графік [рис.5.частина 4 даної к. Р.]. Таблиця 2.
Побудувавши другий графік визначаємо значення Тривалість імпульсу з кодуванням : 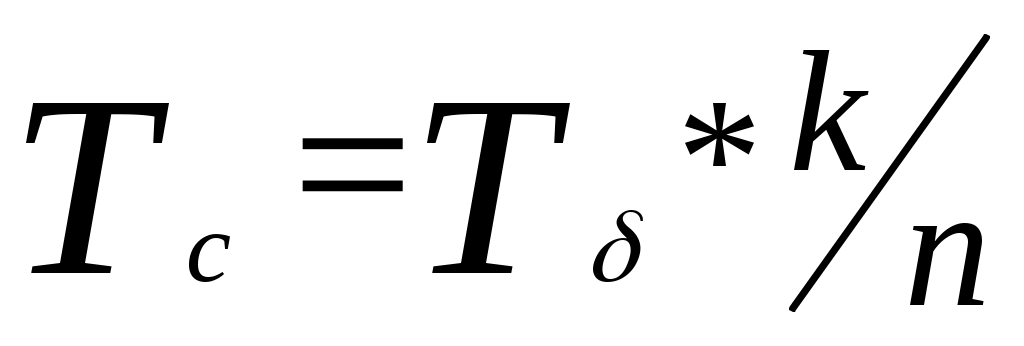 , підставимо значення , підставимо значення Відношення сигнал-шум : 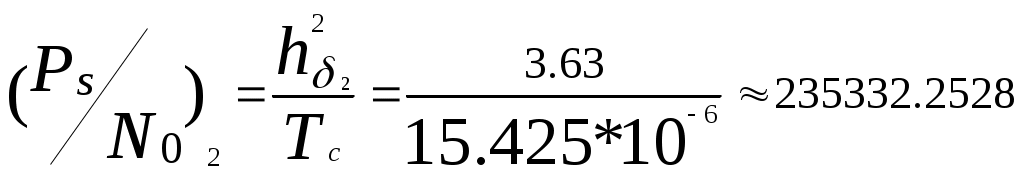 6. Розрахунок основних параметрів аналогової системи передачі. Для вибору індексу частотної модуляції ми повинні порівняти значення 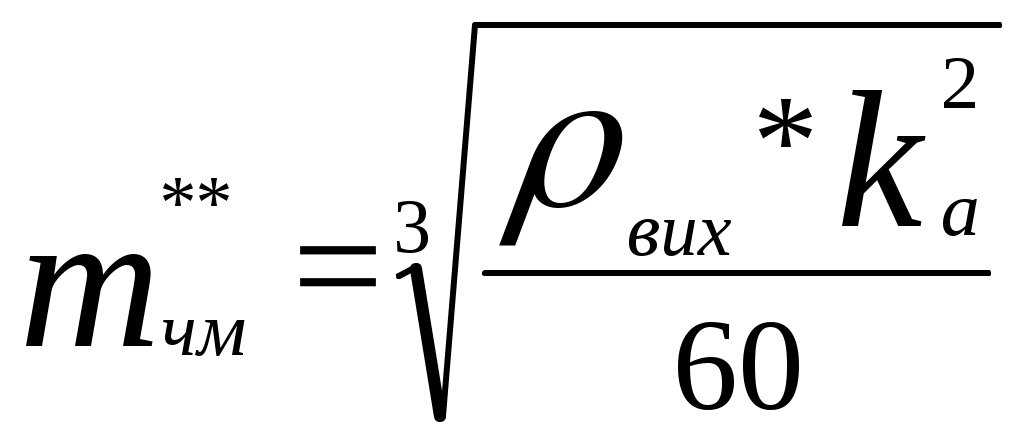 , (6.1) , (6.1)При частотній модуляції виграш знаходимо за формулою 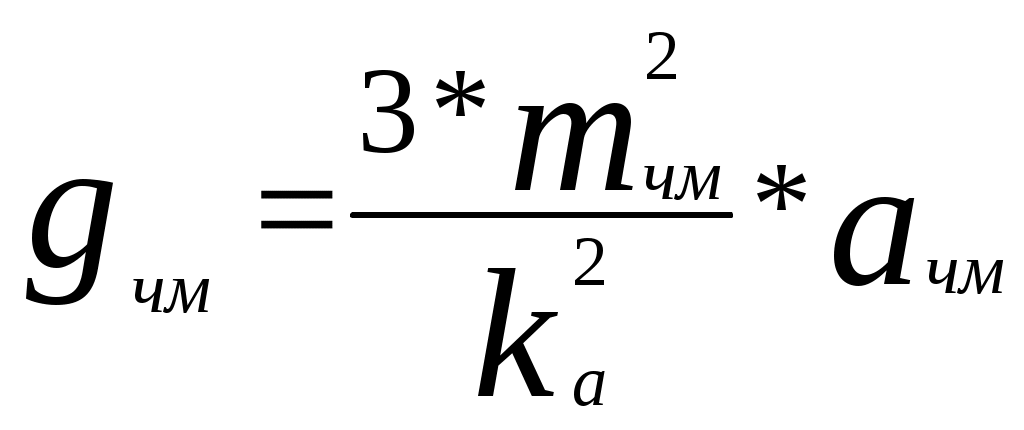 , (6.2) , (6.2)де 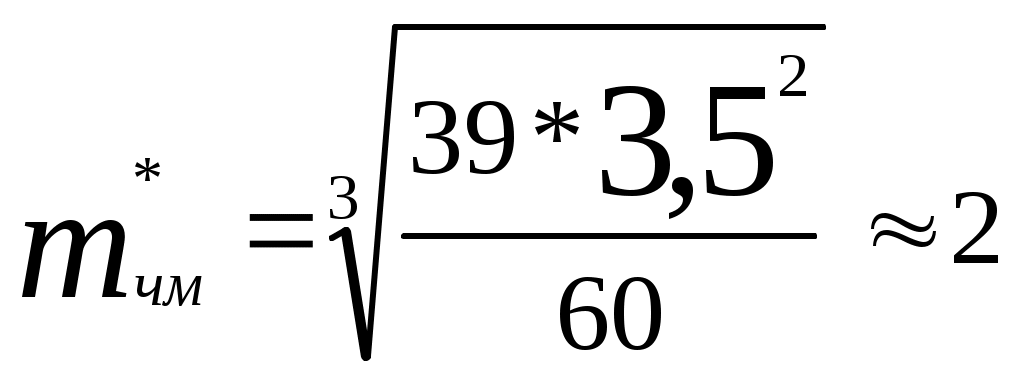 , ,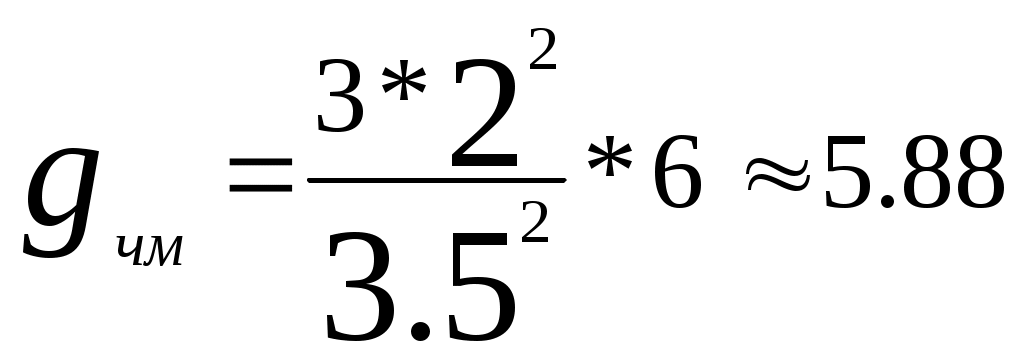 - виграш демодулятора за умови, що - виграш демодулятора за умови, що Залежність 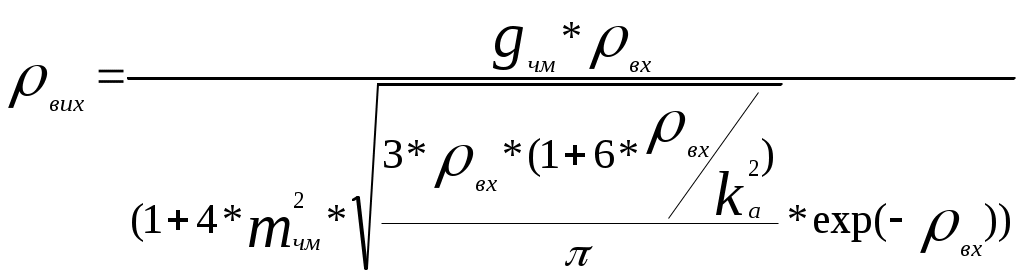 , (6.3) Будуємо графіки залежностей Таблиця 3.
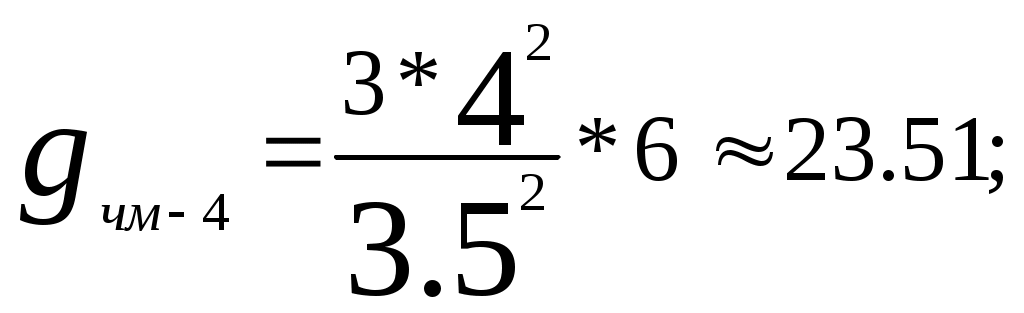 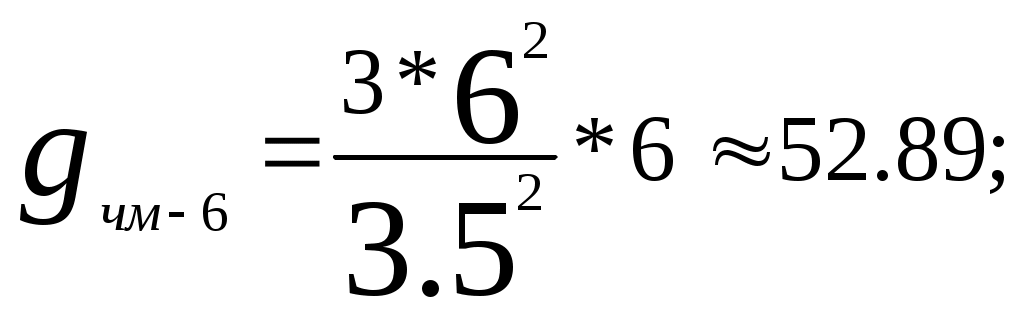 Знайдемо смугу пропускання каналу зв’язку : звідси отримуємо вираз для 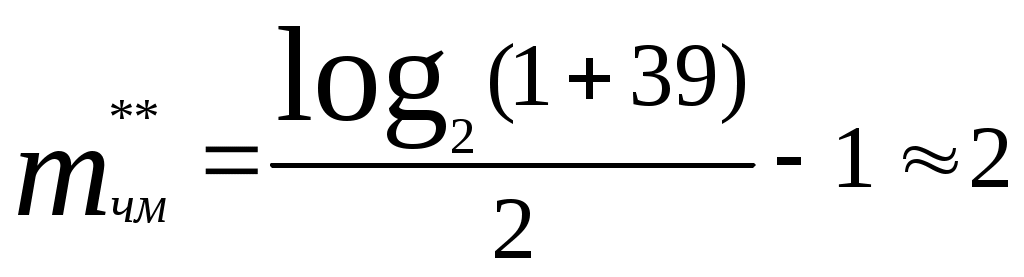 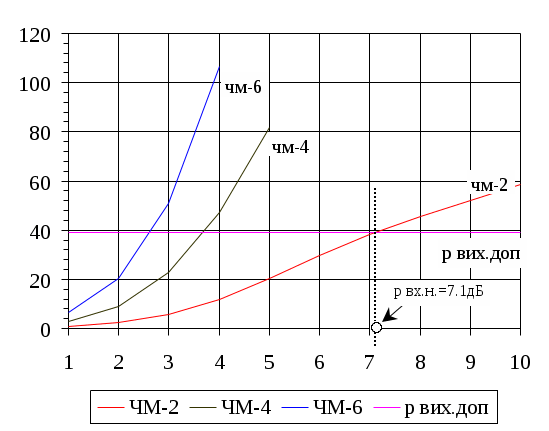 Рис.6 Графік залежності Зобразимо структурну схему аналогової системи передачі методом ЧМ.  Рис. 7 Структурна схема аналогової системи передачі методом ЧМ. |
