Курсова. Розрахунки й оптимізація характеристик
 Скачать 0.54 Mb. Скачать 0.54 Mb.
|
У сигналів з середнім значенням bmin =bmax . Значення bmax визначається по формулі:bmax= 9.5*1.4 = 11.24, відл. b=2*11.24 / 256 = 0.087 B Знайдемо 2 та кв2 : (вих=100,1*3.7=5011.87) 2= 1.4 / 5011.87 = 0.279 мВт кв2 = 1.4 / 20695.57 = 0.067 мВт Звідси х.і.2 = 0.279 - 0.067 = 0.212 мВт Згідно формули (2.6) виразимо доп : 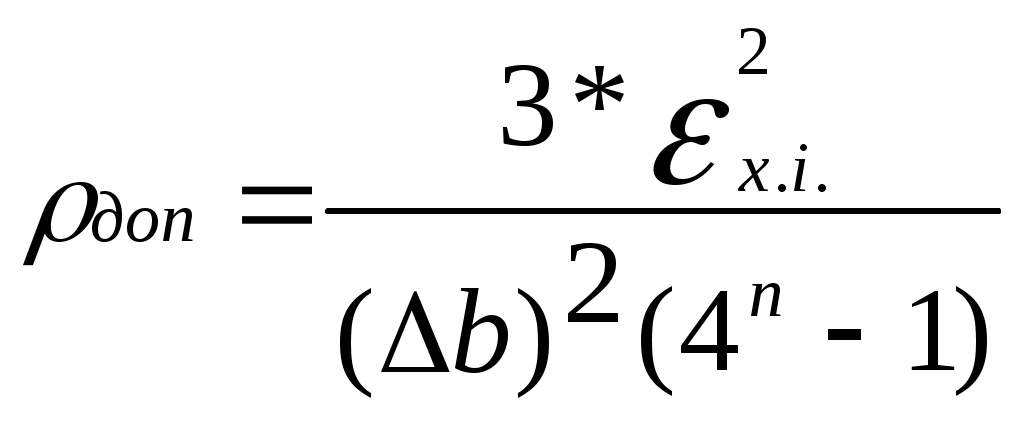 ; ;доп = 3 * 0.212*10-3 / (0.087)2 * (49 – 1) = 0.31*10-6; Розрахунки інформаційних характеристик джерела повідомлень і первинних сигналів. Повідомлення неперервного джерела перетворюється в первинний аналоговий сигнал b(t) за звичай без втрати інформації , тому розрахунки ін формаційних характеристик джерела будемо проводити для первинного сигналу. 1) Епсилон-ентропія розраховується за формулою: 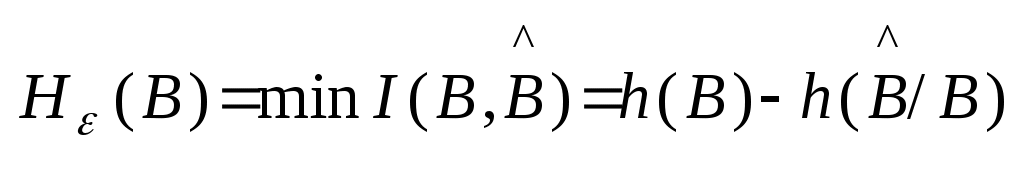 (3.1) (3.1)h(B)-диференційна ентропія Диференціальна ентропія залежить від виду розподілу імовірності P(b) та дисперсії сигналу Так як середнє значення первинного сигналу дорівнює нулю, то 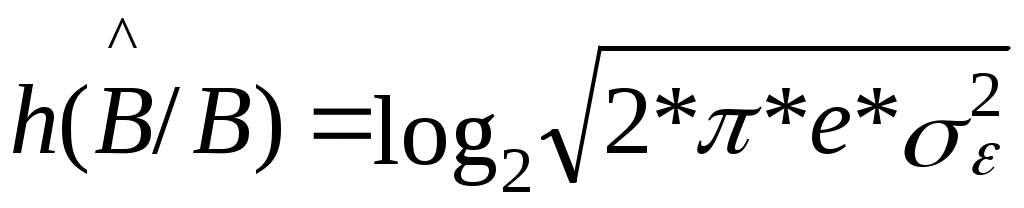 (3.3) (3.3)де Підставимо формули 3.3 та 3.2 в формулу 3.4, одержимо вираз для визначення епсилон-ентропії ,при цьому переведемо дБ в рази 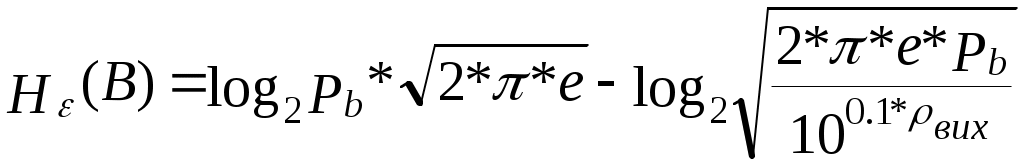 (3.4). (3.4).Підставивши числові значення, одержимо : 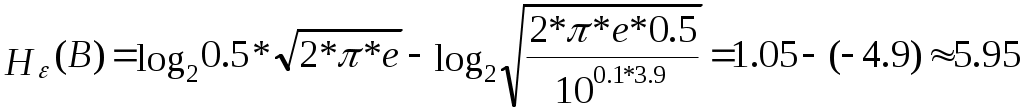 біт/відлік біт/відлік2) Коефіцієнт надлишку джерела обчислюється за формулою : ǽ 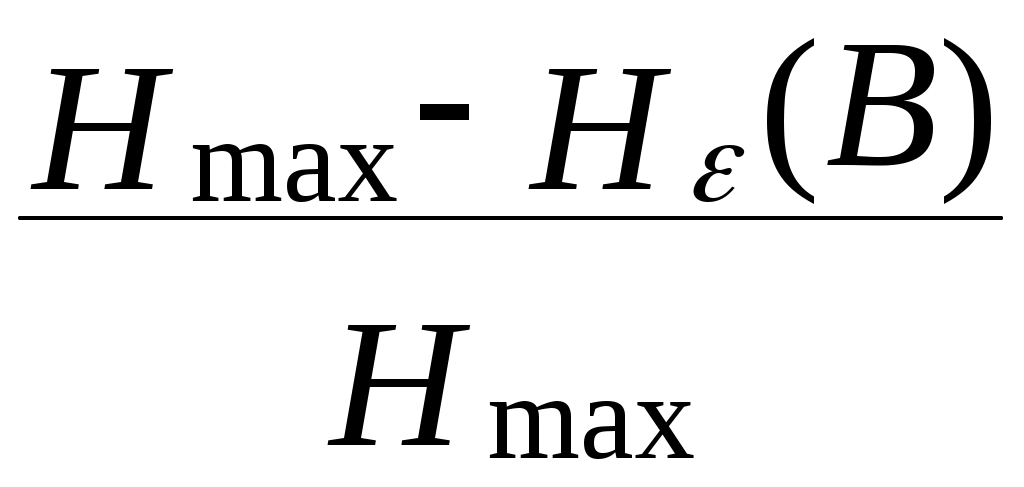 , де , де 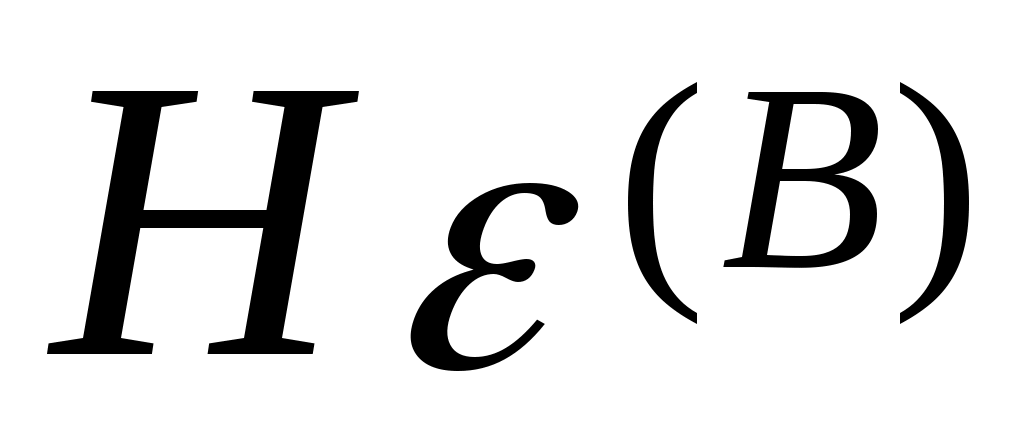 - епсилон-ентропія джерела ; - епсилон-ентропія джерела ; З вище розрахованого отримуємо ǽ= 3) Продуктивність джерела Причини надлишковості джерела : Під надлишковістю розуміють щось лишнє. Надлишковими в джерелі вважаються ті повідомлення, які переносять малу, а іноді і нульову кількість інформації. Час на їхню передачу затрачується, а інформації передається мало. Присутність надлишковості означає, що частину повідомлень можна і не передавати по каналу зв’язку, а відновити на прийомі по відомим статистичним зв’язкам. Основними причинами надлишковості являються : Будь-які імовірності окремих повідомлень. Присутність статистичних зв’язків між повідомленнями джерела. Вимоги до пропускної можливості каналу зв’язку. Найбільше значення швидкості R передачі інформації по каналу зв’язку при заданих обмеженнях називають пропускною можливістю каналу, яка вимірюється в [біт/с] : Під заданими обмеженнями розуміють тип каналу (дискретний або неперервний ) , характеристики сигналів та завад . Пропускна можливість каналу зв’язку характеризує потенційні можливості передачі інформації. Вони описані в фундаментальній теоремі теорії інформації, відомій як основна теорема кодування К.Шенона. Для дискретного каналу вона формулюється слідуючим чином : якщо продуктивність джерела Пропускна можливість каналу, як граничне значення безпомилкової передачі інформації, являється одною з основних характеристик будь-якого каналу. Знаючи пропускну можливість каналу та інформаційні характеристики повідомлень (первинних сигналів) можна передавати по заданому каналу. 4. Розрахунок завадостійості демодулятора. Імовірність помилки двійкового символу для ФМ-2 при оптимальному когерентному прийомі обчислюється за формулою : h- відношення енергії сигналу, що затрачується на передачу одного двійкового символу Ec до питомої потужності шуму N0. Результати розрахунків імовірність помилки двійкового символу заносимо в таблицю 1. Таблиця 1.
|
