|
|
математика теория к контрольным 1 курс 1 семестр. шпора по матану. С доквом) и второй (без доква)
1.Предел функции в точке. Бесконечно малые функции и их свойства (без док-ва).
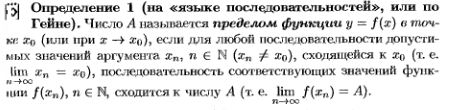
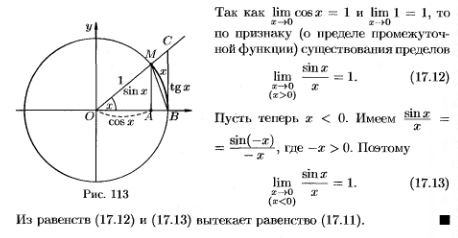
3.Первый (с док-вом) и второй (без док-ва) замечательные пределы.
   
|
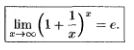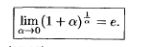
2. Свойства конечных пределов (с док-вом св-в суммы, произведения, частного).
       
|
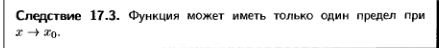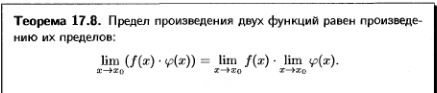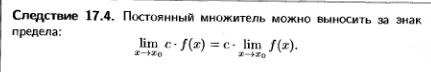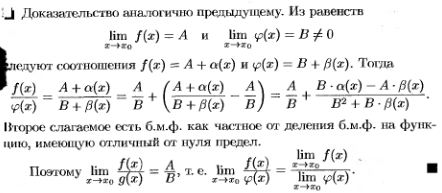
4.Непрерывность функции. Точки разрыва функции и их классификация.
    
 
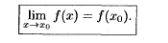
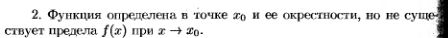
5.Определение производной и ее геометрический смысл.
 
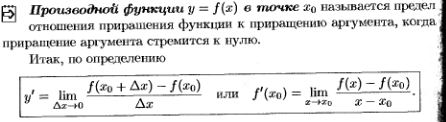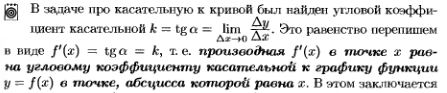
6.Уравнения касательной и нормали (с выводом).
   
|
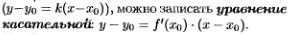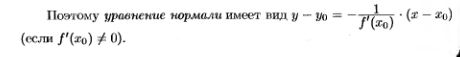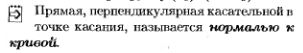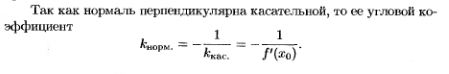
7.Таблица производных. Вывод производных следующих функций:  .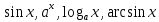
     
|
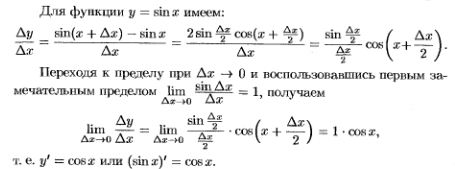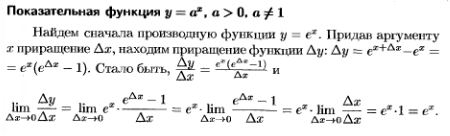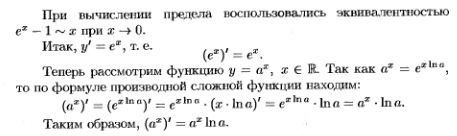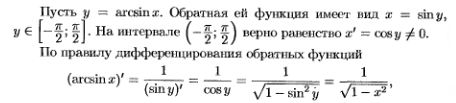
8.Правила дифференцирования (с док-вом).
     
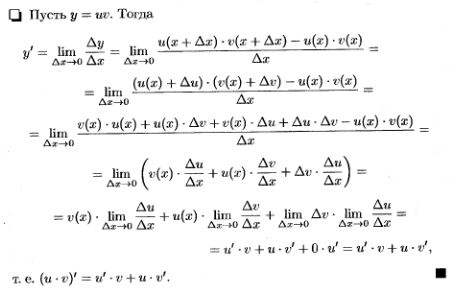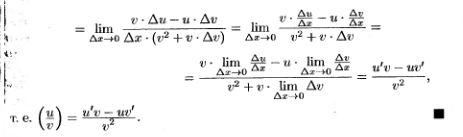
12. Свойства функций, непрерывных на отрезке. Теоремы Ролля и Лагранжа (с док-вом).
   
15.Монотонность функции на промежутке. Необходимые и достаточные условия монотонности функции (с док-вом).
  
Функция возрастает на определенном промежутке, если на этом промежутке большему значению аргумента соответствует большее значение функции.
Функция убывает на определенном промежутке, если на этом промежутке большему значению аргумента соответствует меньшее значение функции.
|
9.Определение дифференцируемости функции. Теорема о связи непрерывности и дифференцируемости (с док-вом).
Функция y=f(x), имеющая производную в каждой точке интервала (a;b), называется дифференцируемой в этом интервале. Операция нахождения производной функции называется дифференцированием.
10. Определение дифференцируемости функции. Теорема о связи дифференцируемости с существованием производной (с док-вом).
Функция y=f(x), имеющая производную в каждой точке интервала (a;b), называется дифференцируемой в этом интервале. Операция нахождения производной функции называется дифференцированием.
11 Дифференциал функции. Инвариантность формы дифференциала первого порядка (с док-вом).
 
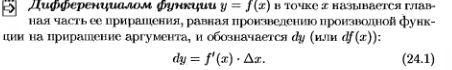
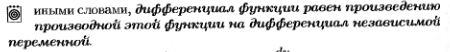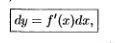
13. Правило Лопиталя для раскрытия неопределенностей вида (без док-ва).
 
14.Теорема о производной сложной функции (с док-вом).
16. Экстремумы функции. Необходимые и достаточные условия экстремумов (с док-вом).
Экстремум - максимальное или минимальное значение функции на заданном множестве.
Точка экстремума - точка, в которой достигается экстремум.
  19. Определение первообразной. Теорема об общем виде первообразной (с док-вом).
 
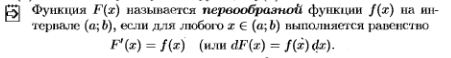
20. Определение неопределенного интеграла, его свойства (без док-ва).
     
|
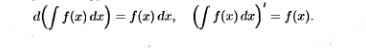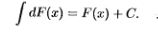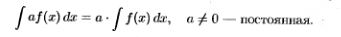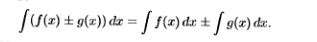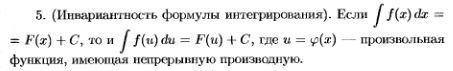
17. Выпуклость, вогнутость. Точки перегиба графика функции. Достаточные условия выпуклости, вогнутости и точек перегиба графика функции (с док-вом).
   
|
23. Определенный интеграл: определение и геометрический смысл.
  
24.Свойства определенного интеграла. Теорема о среднем значении (с док-вом).
           
|
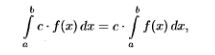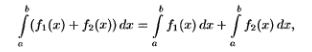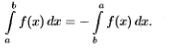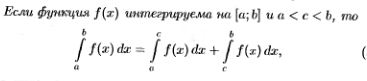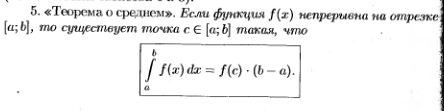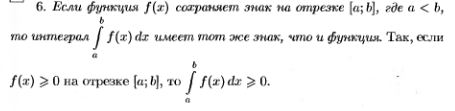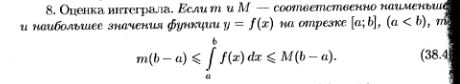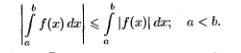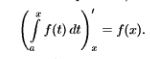
26.Формула Ньютона-Лейбница (с док-вом).
  
|
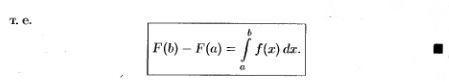
27. Замена переменной (с док-вом) и интегрирование по частям в определенном интеграле (без док-ва).
  
| |
|
|
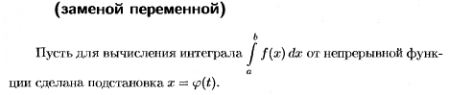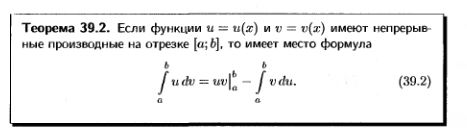
Скачать 2.03 Mb.