Физика ИТМО лабораторная работа 1. Сафонова Арина Олеговна Работа выполнена Преподаватель Афанасьева Т. В. отчет принят Рабочий протокол и отчет
 Скачать 114.98 Kb. Скачать 114.98 Kb.
|
|
Санкт-Петербургский национальный исследовательский университет информационных технологий, механики и оптики  Группа Р3123 К работе допущен Студент Сафонова Арина Олеговна Работа выполнена Преподаватель Афанасьева Т.В. Отчет принят Рабочий протокол и отчет по лабораторной работе №1  Исследование распределения случайной величины  Цель работы. 1) Провести многократные измерения определенного интервала времени. 2) Построить гистограмму распределения результатов измерения. 3) Вычислить среднее значение и дисперсию полученной выборки. 4) Сравнить гистограмму с графиком функции Гаусса с такими же, как и у экспериментального распределения средним значением и дисперсией. Задачи, решаемые при выполнении работы. Провести 50 измерений, устанавливая промежуток времени в 5с. Результат каждого измерения заносить во второй столбец Табл. 1; Построим гистограмму, выполняя следующие действия: - взять tmin и tmax из Табл. 1. - разбить промежуток на m равных интервалов, где m должно быть близко к 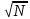 (N – число измерений). Измеренные значения 𝑡𝑚𝑖𝑛 и 𝑡𝑚𝑎𝑥 должны попадать внутрь «крайних» интервалов; Границы выбранных интервалов занесем в первый столбец Табл. 2 (N – число измерений). Измеренные значения 𝑡𝑚𝑖𝑛 и 𝑡𝑚𝑎𝑥 должны попадать внутрь «крайних» интервалов; Границы выбранных интервалов занесем в первый столбец Табл. 2- подсчитаем число результатов измерений ∆𝑁𝑖, из Табл. 1, попавших в каждый из интервалов ∆𝑡, заполнив таким образом второй столбец Табл. 2; – вычислим опытное значение плотности вероятности (третий столбец Табл. 2); – построим на миллиметровой бумаге гистограмму. По данным Табл. 1 вычислим выборочное значение среднего ⟨𝑡⟩𝑁 и выборочное среднеквадратичное отклонение 𝜎𝑁; Запишем результат «в подвал» Табл.1; По формуле (5) вычислите максимальное значение плотности распределения 𝜌𝑚𝑎𝑥, соответствующее 𝑡 = ⟨𝑡⟩, занесите его в «подвал» Табл. 1; Найдем значения 𝑡, соответствующие серединам выбранных ранее интервалов, занесем их в четвертый столбец Табл. 2. Для этих значений, используя параметры ⟨𝑡⟩𝑁 и 𝜎𝑁 в качестве ⟨𝑡⟩ и 𝜎, вычислим значения плотности распределения 𝜌 (𝑡), занесем их в пятый столбец Табл. 2. Нанесем все расчетные точки на график, на котором изображена гистограмма, и проведем через них плавную кривую; Проверим, насколько точно выполняется в наших опытах соотношение между вероятностями и долями 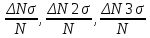 . Для этого вычислим границы интервалов для найденных вами значений ⟨𝑡⟩𝑁 и 𝜎𝑁, занесем их во второй и третий столбцы Табл. 3; . Для этого вычислим границы интервалов для найденных вами значений ⟨𝑡⟩𝑁 и 𝜎𝑁, занесем их во второй и третий столбцы Табл. 3;По данным Табл. 1 подсчитаем и занесем в Табл. 3 количество ∆𝑁 измерений, попадающих в каждый из этих интервалов, и отношение 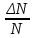 этого количества к общему числу измерений. Сравним их с соответствующими нормальному распределению значениями 𝑃 вероятности; этого количества к общему числу измерений. Сравним их с соответствующими нормальному распределению значениями 𝑃 вероятности;Рассчитаем среднеквадратичное отклонение среднего значения; Найдем табличное значение коэффициента Стьюдента 𝑡𝛼,𝑁 для доверительной вероятности 𝛼 = 0,95. Запишем доверительный интервал для измеряемого в работе промежутка времени. Объект исследования. Промежуток времени длительностью в 5 секунд Метод экспериментального исследования. Стрелочным секундомером задается интервал времени, который многократно измеряется цифровым секундомером Рабочие формулы и исходные данные.
Измерительные приборы.
Результаты прямых измерений и их обработки (таблицы, примерырасчетов).
Расчет результатов косвенных измерений (таблицы. примерырасчетов).
Δt = 0.0825 Расчет погрешностей измерений (для прямых и косвенныхизмерений).
Графики (перечень графиков. которые составляют Приложение2). Выводы и анализ результатов работы. Так как в данном эксперименте большую роль играл человеческий фактор и неконтролируемые факторы (ручное нажатие кнопки секундомера), то гистограмма и кривая имеют отличия с нормальным распределением Гаусса. Также на результат повлияла малая выборка: при большем количестве измерений обработанные данные были бы точнее. Однако, можно заметить, что они имеют схожую динамику. Дополнительные задания. Выполнение дополнительных заданий. Замечания преподавателя (исправления, вызванные замечаниями преподавателя, также помещают в этот пункт. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

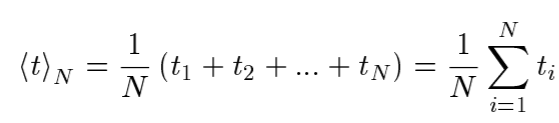
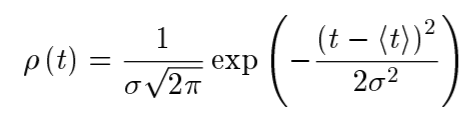
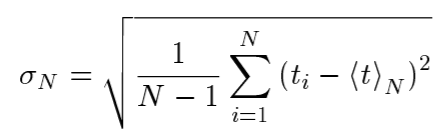
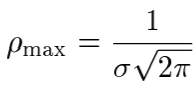
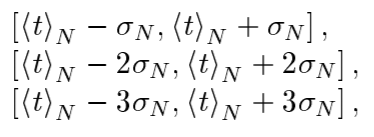
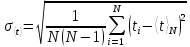
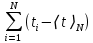 = -8Е-15
= -8Е-15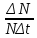 . c-1
. c-1