критерий пирсона. Критерий пирсона
 Скачать 37.87 Kb.
|
КРИТЕРИЙ ПИРСОНАВ соответствии с критерием, область в пределах которой лежат значения выборки случайных величин xi, i=1,2,......,n, разбивается на m интервалов (не обязательно равных). Положим для простоты, что интервалы одинаковы, тогда длина интервала будет равна  .Обозначим через mkчисло попаданий случайной величины xi в k- тый интервал K, тогда случайная величина 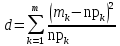 ,где  вероятность попадания случайной величины x в k-тый интервал  .WT- аналитическое выражение для плотности вероятности случайного процесса, на соответствие которой проверяют экспериментальные данные. При достаточно большом объеме выборки n30 случайная величина  будет распределена по закону хи - квадрат с числом степеней свободы, равным ,где r - число связей, определяемых, как число параметров теоретической плотности вероятности, вычисляемых по выборке случайной величины. Рис.1. Так, например, для задания нормального закона распределения необходимо знать два параметра - математическое ожидание и дисперсию. Если значения математического ожидания и дисперсии неизвестны до эксперимента, то их оценки определяют из выборки случайной величины и, следовательно, r равно 2. При использовании критерия Пирсона гипотеза о том, что экспериментальные данные имеют теоретический закон распределения, принимается, если  , где 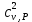 табличное значение распределения хи - квадрат с степенями свободы и доверительной вероятностью, равной Р. В противном случае гипотеза отвергается.Недостатком критерия Пирсона является то, что экспериментальные данные необходимо разбивать на группы, а поскольку строгого критерия, в соответствии с которым это можно было бы сделать нет, то возникает определенный субъективизм при применении этого критерия. В литературе по метрологии предлагаются различные критерии выбора числа интервалов m  и другие. Список использованной литературы: Пастушков, А. А. КРИТЕРИЙ ПИРСОНА / А. А. Пастушков [Текст] // Метрологическое обеспечение средств измерений: Учебное пособие / Московский государственный институт радиотехники, электроники и автоматики (Технический университет). — Москва:Печатается по решению редакционно-издательского совета Московского государственного института радиотехники, электроники и автоматики (Технический университет)., 1996. — С. 114-115. |