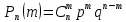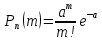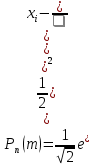Экология. Самостоятельная работа 2 Расчет основных показателей описательной статистики
 Скачать 21.9 Kb. Скачать 21.9 Kb.
|
|
Асипенко Илья Игоревич 18НПД-1 Управляемая самостоятельная работа №2 Расчет основных показателей описательной статистики Случайной величиной называют переменную величину, которая в одних и тех же условиях принимает различные числовые значения, зависящие от случая. Случайная величина называется дискретной, если она может принимать только целые значения. Случайная величина, принимающая все значения из некоторого промежутка, называется непрерывной случайной величиной. Значения случайных величин невозможно предугадать даже при полностью известных условиях эксперимента, в котором они измеряются. Можно лишь указать вероятности того, что случайная величина принимает то или иное значение или попадает в то или иное множество. Законом распределения случайной дискретной величины (X) называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. К дискретным относятся распределение Бернулли, биномиальное и пуассоновское распределения. Распределение Бернулли используется для того, чтобы определить вероятность успешного исхода при одном испытании. Биномиальное распределение используется для определения вероятности появления определенного числа успешных исходов при n независимых испытаниях. Распределение Пуассона описывает число событий, происходящих в одинаковых промежутках времени или на одинаковых площадях, при условии, что события происходят независимо друг от друга. К непрерывным распределениям относят нормальное, а также связанные с нормальным распределения: Стьюдента, F – распределение Фишера. Биномиальное распределение. Пусть производится n последовательных независимых одинаковых испытаний, в каждом из которых может наступить или не наступить событие А. Вероятность наступления события А в каждом испытании – р, а события – q=1–р. Обозначим Рn(m) = р (событие А наступило m раз в n испытаниях). Тогда:
Распределение Пуассона. Если случайная величина X распределена по закону Пуассона, тогда вероятность того, что при n независимых испытаниях она примет определенное значение m, выражается формулой:
Нормальное распределение. В любом симметричном вариационном ряду заметна одна характерная особенность – накапливание вариант в центральных классах и постепенное убывание их численности по мере удаления от центра ряда. Таким образом, прослеживается широко распространенная в природе закономерность: в статической совокупности большинство вариант оказывается среднего или близкого к нему размера, чем дальше они отстоят от среднего значения, тем реже встречаются в данной совокупности. Такая закономерность описывается законом нормального распределения. Функцией Гаусса-Лапласа (нормальное распределение):
Для нормального распределения характерно совпадение по абсолютной величине средней арифметической, медианы и моды. Равенство между этими показателями указывает на нормальность данного распределения. Для кривой нормального распределения характерно, что на равные интервалы, измеряемые стандартным отклонением от центра распределения, приходится равное число вариант. Закон больших чисел и центральная предельная теорема. Практика изучения случайных явлений показывает, что хотя результаты отдельных наблюдений, проведенных в одинаковых условиях, могут сильно отличаться, средние результаты для достаточно большого числа наблюдений устойчивы и слабо зависят от результатов отдельных наблюдений. Теоретическим обоснованием этого свойства случайных явлений является закон больших чисел, который утверждает, что при определенных, достаточно общих условиях, с увеличением числа случайных величин (объема выборки) их выборочное среднее арифметическое стремится к генеральной средней величине и перестает быть случайным. Центральная предельная теорема утверждает, что всегда, когда случайная величина образуется в результате сложения большого числа независимых случайных величин с конечными дисперсиями, закон распределения этой случайной величины оказывается практически нормальным законом. |