202163_б2-СТЗСз-31_Астарханов. Самостоятельная работа По дисциплине Проектирование гражданских зданий
 Скачать 1.27 Mb. Скачать 1.27 Mb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное образовательное учреждение высшего образования «Саратовский государственный технический университет имени Гагарина Ю.А.» Кафедра: «Строительные материалы, конструкции и технологии» (СМКТ) Самостоятельная работа По дисциплине «Проектирование гражданских зданий» Вариант № 1 Выполнил студент группы: Б-СТЗСз-31 Астарханов Р.А. Шифр: 202163 Проверил: ст. преп.каф. СМКТ: Пименов Д.А. Саратов 2023 СодержаниеЛист задания 3 Задание 1 3 Задание 2 6 Задание 3 13 Задание 4 19 Задание 5 25 Задание 6 25 Заключение 26 Список литературы 27
Задание №1 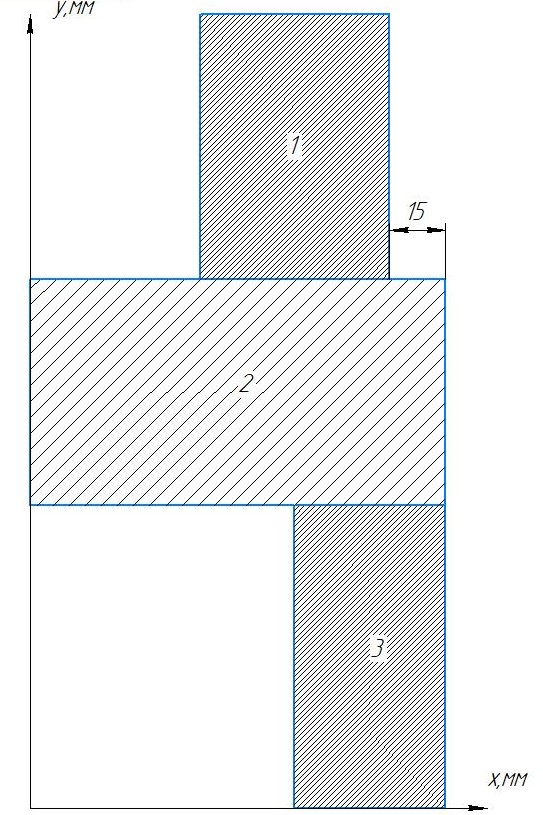 Рис.1- Поперечное сечение конструкции Решение 1)Для определения статистического момента площади поперечного сечения конструкции (ПСК) расположим оси х и у согласно рис.1 Для интегрального выражения координат центра тяжести воспользуемся формулой: Ус= 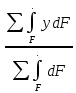 (1) (1)где выражение в числителе дроби значит интегральная сумма от произведения бесконечно малой площадки dF на расстояние от её центра тяжести до оси х. А в знаменателе интегральная сумма от площади ПСК из множества бесконечно малых площадок dF Аналогичное выражение для хс хс= 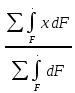 (2) (2)Так как большинство известных строительных сечений состоят из простых сечений, то формулы (1) и (2) можно выразить так: ус= 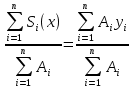 (3) (3)xс= 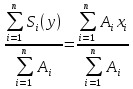 (4) (4)Итого, статический момент площади ПСК для выбранного вариант будет вычислен следующим образом: ус= 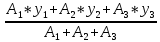 = =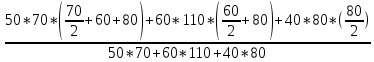 =110мм =110ммхс= 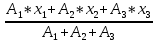 = =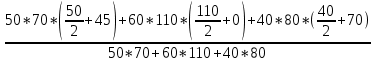 =67мм =67ммКоординаты центра тяжести ПСК: хс=67 мм ус=110 мм 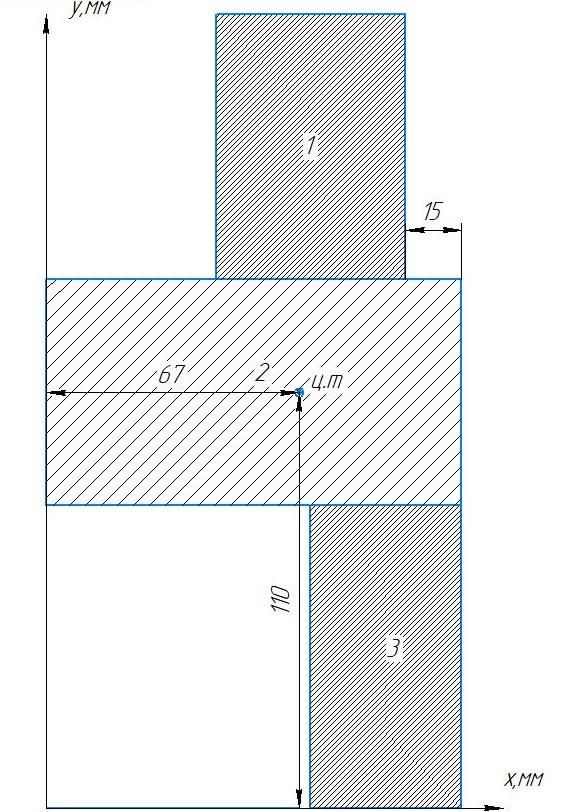 Рис 2- центр тяжести сложного поперечного сечения конструкции 2)Осевой момент инерции ПСК относительно его центра тяжести для осей у и х выразим в интегральном виде, как: Jx= 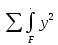 dF ; Jy= dF ; Jy=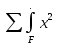 dF dFТакже интегрально выразим центробежный момент инерции ПСК: Jyх= 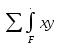 dF; dF;Так как для центры тяжести размеров 1-3 не совпадают с центром тяжести ПСК, то при вычислении Jx, Jy, Jyх учтём добавление соответственно: 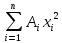 ; ;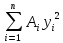 ; ; 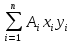 Следовательно, значение этих характеристик ПСК, используя известную формулу для прямоугольников вида 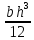 , находим, как: , находим, как:Jy= 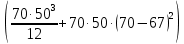 + +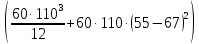 + +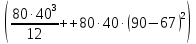 =10 485 533 мм^4 =10 485 533 мм^4Jx 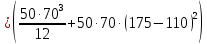 + +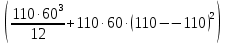 + +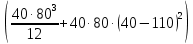 =35 583 333 мм^4 =35 583 333 мм^4Jyх= 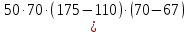 + +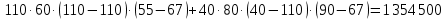 мм^4 мм^4Итого в см^4 Jx 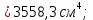 Jy=1048,6 см^4 ; Jyх=1354,5 . Jy=1048,6 см^4 ; Jyх=1354,5 .3) Момент сопротивления изгибу ПСК находим для верхнего и нижнего крайних волокон, как: 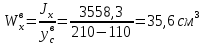 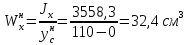 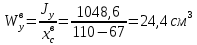 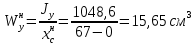 Задание №2 Конструктивный элемент 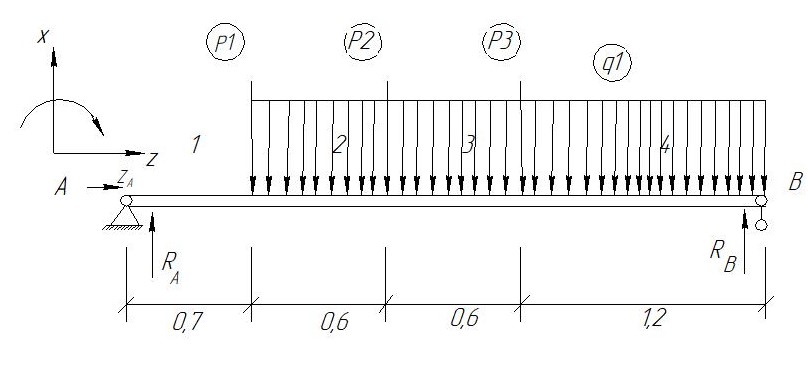 Рис 3-Конструктивный элемент Дано: Р1=100 кг Р2=110 кг Р3=50 кг q1=25 кг/м Решение: 1) ОХ: 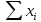 =0 ; =0 ;ОZ: 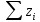 =0 ; =0 ;MA: 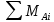 =0 ; =0 ;Выше приведены условия равенства нагрузок и опорных реакций нулю составляют три уравнения статики. Решением этой системы уравнений и будут искомые опорные реакции. Выразим эти условия для данного варианта: 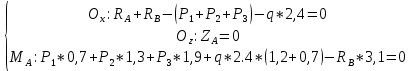 Из 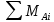 =0 получаем =0 получаем 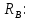 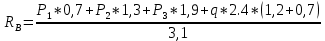 =242,03 кгс =242,03 кгсПодставляя в 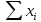 =0, получим =0, получим 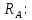 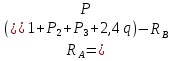 =287,2кгс =287,2кгсИтого 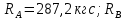 = =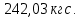 2)Для определения поперечных сил в балке разделим её на 4 сектора Сектор 1-1 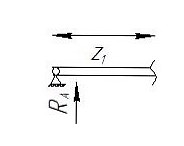 Рис 4-Исследуемый участок №1 Q( 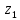 )= )=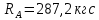 Сектор 2-2 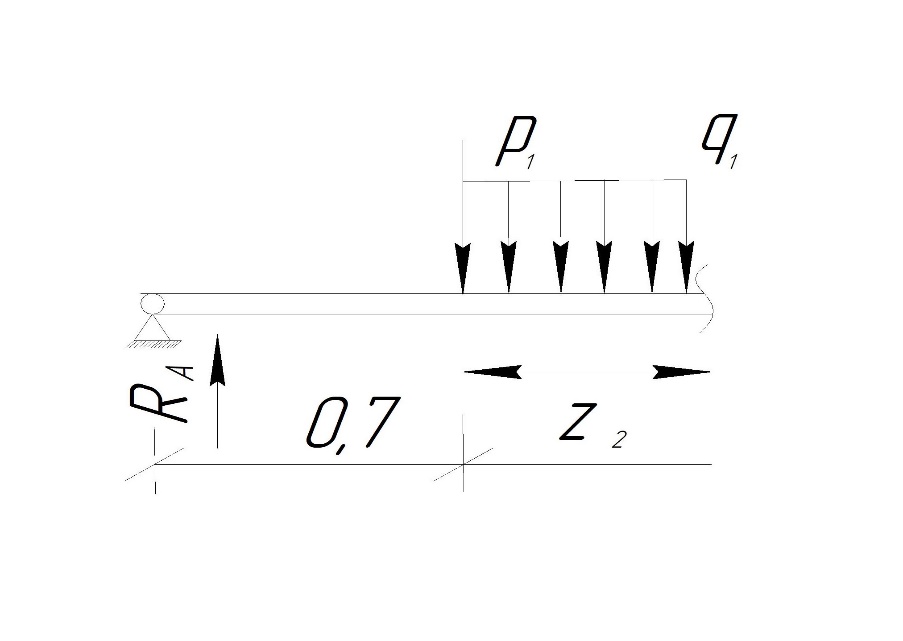 Рис 5-Исследуемый участок №2 Q( 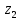 )= )=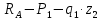 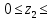 0,6м 0,6мQ(  )= )=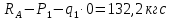 Q( 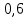 )= )=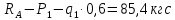 Сектор 3-3 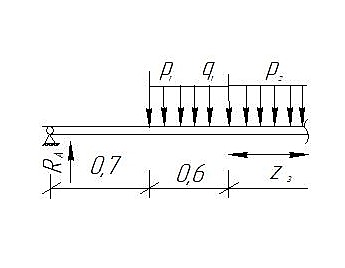 Рис 6-Исследуемый участок № 3 Q( 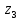 )= )=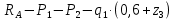 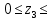 0,6м 0,6мQ(  )= )=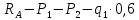 =-6,6 кгс =-6,6 кгсQ( 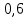 )= )=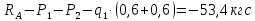 Сектор 4-4 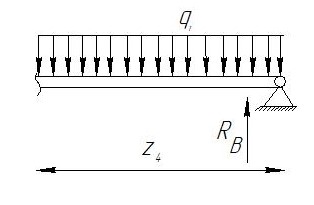 Рис 5-Исследуемый участок №4 Q( 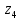 )= )=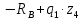 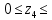 1,2м 1,2мQ(  )= )=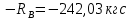 Q( 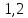 )= )=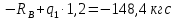 По полученным значениям поперечных сил в характерных точках балки построим эпюру этих сил: 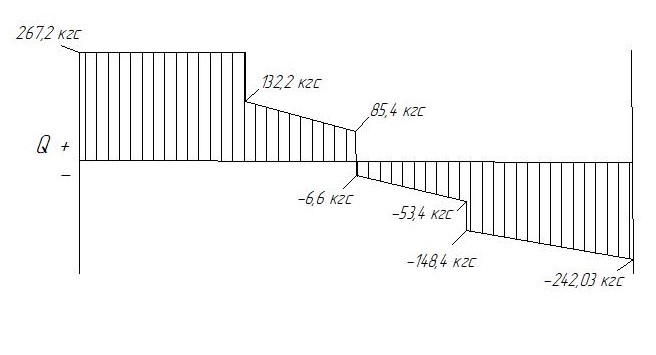 Рис 6- Эпюра поперечных сил 3) По тому же методу определим значение изгибающих моментов, возникающих в точках балки: Сектор 1-1  M( 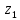 )= )=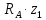 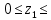 0,7м 0,7мM(  )= )= 0 кгс 0 кгс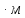 M( 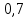 )= )=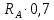 =187,0 кгс =187,0 кгс Сектор 2-2 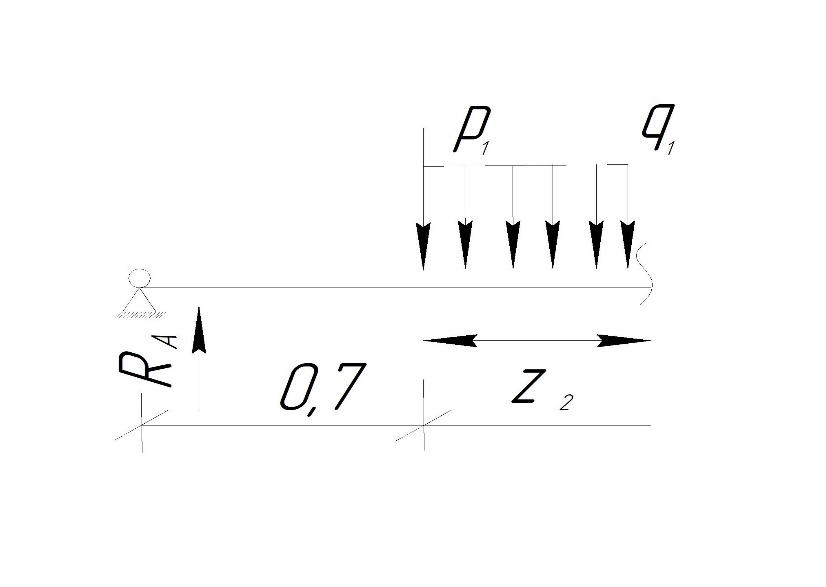 M( 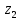 )= )=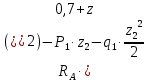 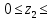 0,6м 0,6мM(  )= )=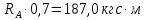 M( 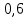 )= )=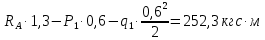 Так как на секторе 2-2 эпюра поперечных сил не является двухзначной , экстремумов функции M( 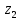 ) на этом секторе нет. ) на этом секторе нет.Сектор 3-3  M( 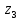 )= )=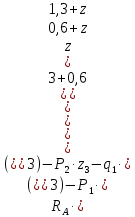 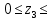 0,6м 0,6мM(  )= )=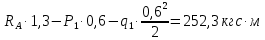 M( 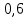 )= )=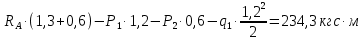 На этом секторе нет экстремумов функции M( 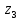 ), т.к. функция Q( ), т.к. функция Q(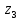 ) не двузначна. Переход от +Q к –Q происходит в пределе границ секторов 2-2 и 3-3,поэтому максимальное значение изгибающего момента будет в этой точке. ) не двузначна. Переход от +Q к –Q происходит в пределе границ секторов 2-2 и 3-3,поэтому максимальное значение изгибающего момента будет в этой точке.Сектор 4-4  M( 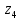 )= )=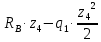  1,2м 1,2мM(  )= )= M(  )= )=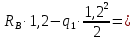 234,2 кгс 234,2 кгс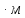 По вычисленным значениям изгибающего момента в балке построим эпюру: 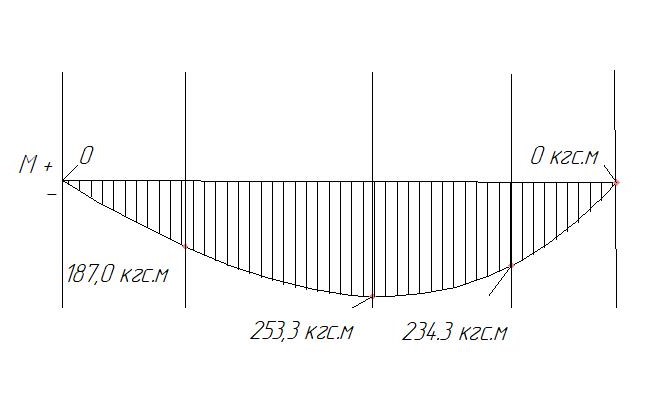 Задание 3 Дано
Условие допустимого напряжения в конструктивном элементе выражается, как:  где 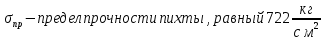 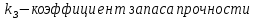 Максимальное значение напряжения 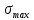 будет определено в зависимости от максимального изгибающего момента , возникающего в балке с учётом всех коэффициентов надёжности для нагрузок. будет определено в зависимости от максимального изгибающего момента , возникающего в балке с учётом всех коэффициентов надёжности для нагрузок.Для этого определим расчётное значение нагрузок: Сосредоточенные: 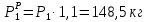 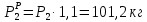 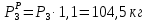 Распределённая: 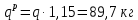 Собственный вес: 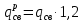 Нормативное значение собственного веса балки определим , как : 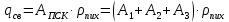 = =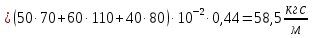 Итак, расчётное значение ,равно: 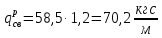 Определим опорные реакции расчётной схемы для нашего варианта по последовательности аналогичной, как в задании №2 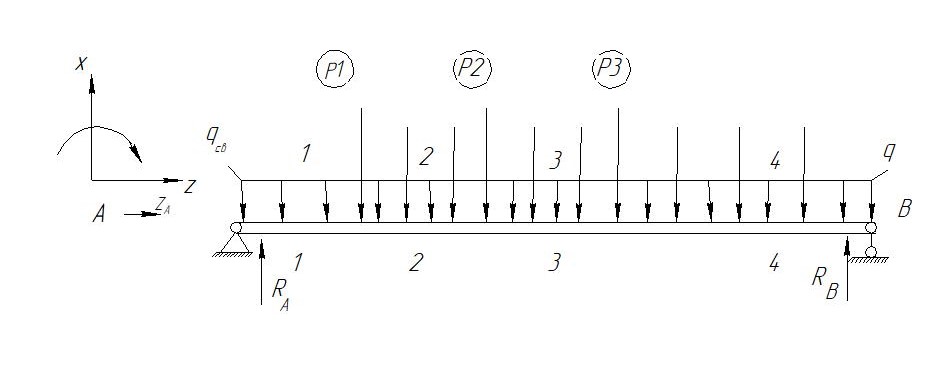 Условие геометрической неизменяемости: ∑ 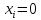 ; ∑ ; ∑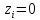 ; ∑ ; ∑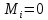 Находим исходные опорные реакции: 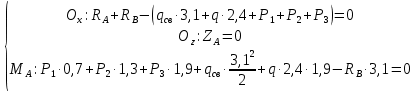 Из 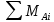 =0 получаем =0 получаем 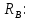 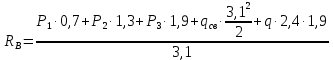 =380,4 кгс =380,4 кгс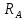 = =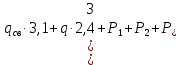 =405,6 кгс =405,6 кгсВеличины поперечных сил изгибающих моментов по секторам будут выражены, так: Сектор 1-1 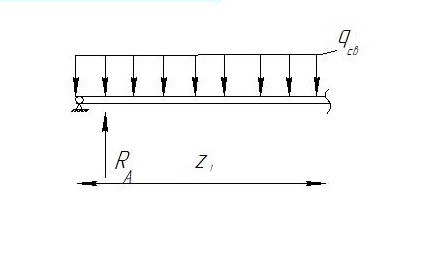 Q(  )= )= 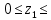 0,7м 0,7мQ(  )= )=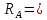 405,6кгс 405,6кгсQ( 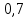 )= )=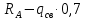 =356,6 кгс =356,6 кгсM( 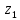 )= )=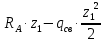 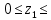 0,7м 0,7мM(  )= )= 0 кгс 0 кгс M( 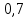 )= )=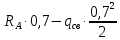 =266,8 кгс =266,8 кгс Сектор 2-2 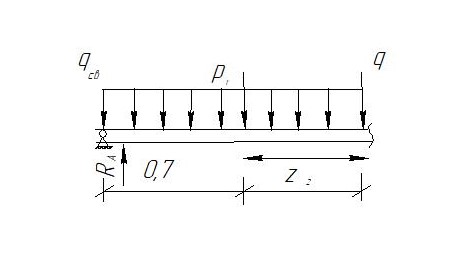 Q( 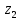 )= )=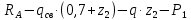 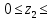 0,6м 0,6мQ(  )= )=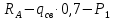 =208,6 кгс =208,6 кгсQ( 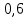 )= )=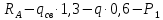 =112,6 кгс =112,6 кгсM( 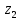 )= )=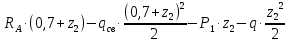 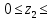 0,6м 0,6мM(  )= )=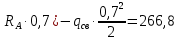 кгс кгс M( 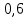 )= )=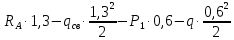 =363,2 кгс =363,2 кгс Сектор 3-3 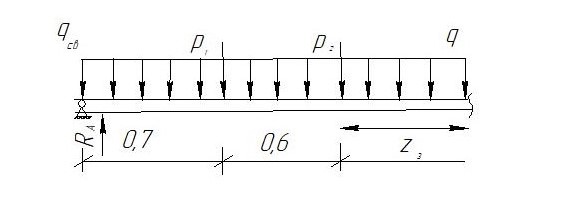 Q(  )= )=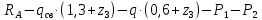 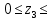 0,6 м 0,6 мQ(  )= )=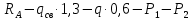 =11,6 кгс =11,6 кгсQ( 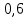 )= )=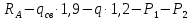 =-84,4 кгс =-84,4 кгсM( 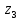 )= )=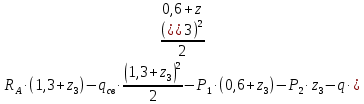 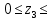 0,6м 0,6мM(  )= )=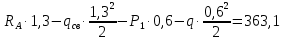 кгс кгс M(  )= )=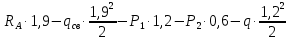 =341,2 кгс =341,2 кгс Сектор 4-4 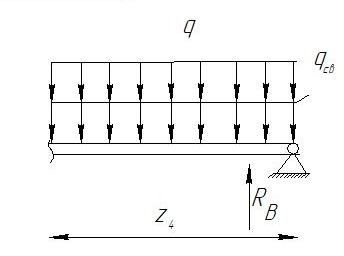 Q(  )= )=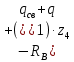 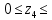 1,2м 1,2мQ(  )= )=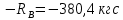 Q(  )= )=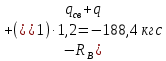 M( 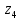 )= )=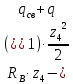 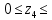 1,2м 1,2мM(  )= )=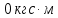 M(  )= )=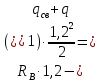 341,3 кгс 341,3 кгс По вычисленным значениям внутренних усилий построим эпюры: поперечных сил Q и изгибающих моментов М 1.Эпюра поперечных сил 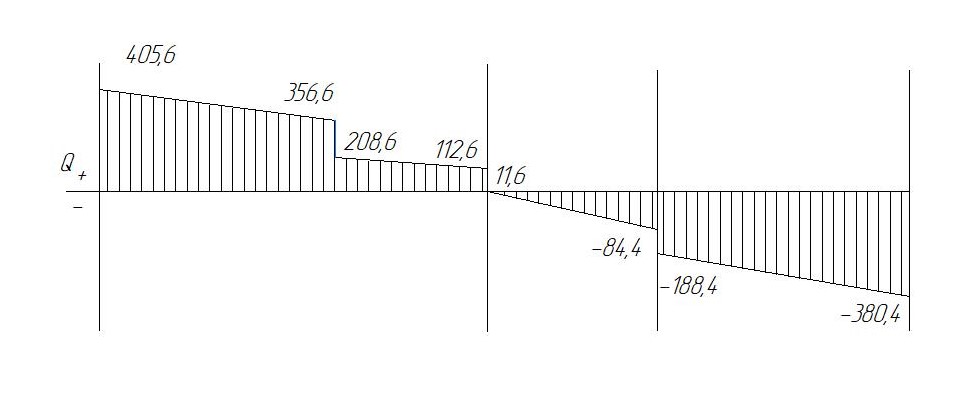 2.Эпюра изгибающих моментов 2.Эпюра изгибающих моментов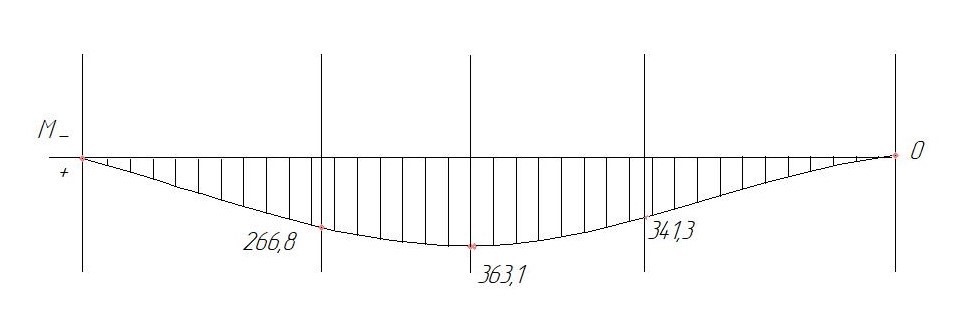 Так как переход +Q к Q переходит фактически в характерной точке под приложением P2. Значит, максимальное значение изгибающего момента, будет в этой точке: Ммах= 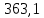 кгс кгс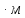 Максимальное напряжение для верхних волокон ПСК выражается, как: 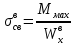 = =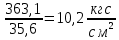 Аналогично для нижних волокон 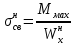 = =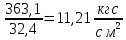 Примем 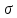 мах= мах=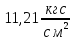 В соответствии с выше приведённом условием: 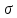 мах= мах=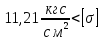 = =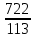 =555,4 =555,4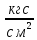 Делаю вывод, что прочность конструктивного элемента при заданном ПСК обеспечена с большим запасом. Задание №4 Также вычислим условия перемещения и прогибы балки от заданных нормативных нагрузок с учётом добавленного собственного веса балки. 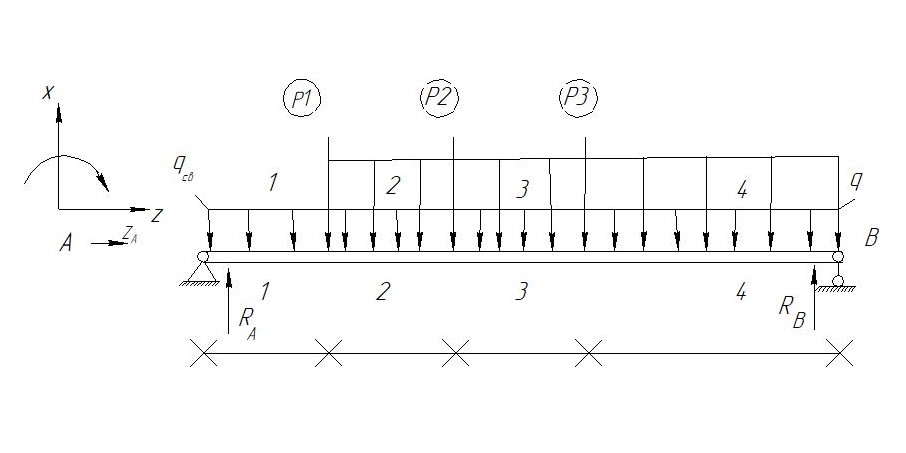 Условие геометрической неизменяемости: ∑  ; ∑ ; ∑ ; ∑ ; ∑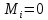 Искомые опорные реакции будут выражены, как : 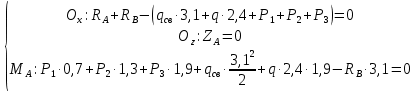 Из 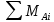 =0 получаем =0 получаем 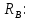 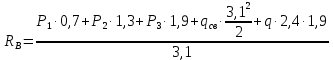 =331,9 кгс =331,9 кгс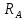 = =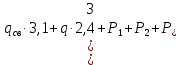 =357,1 кгс =357,1 кгсЗапишем для каждого сектора уравнение поперечных сил, изгибающих моментов, угловых перемещений и прогибов: Сектор 1-1 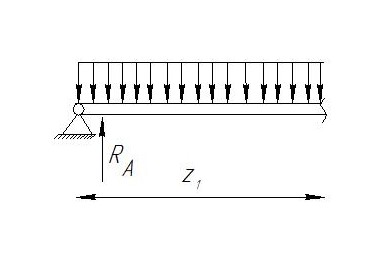 Q( 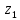 )= )=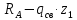 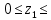 0,7м 0,7мQ(  )= )=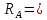 357,1 кгс 357,1 кгсQ( 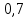 )= )=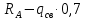 =316,5 =316,5M( 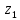 )= )=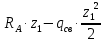 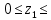 0,7м 0,7мM(  )= )= 0 кгс 0 кгс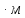 M( 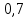 )= )=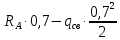 =235,7 кгс =235,7 кгс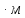 Для шарниров А и В граничные условия по угловым перемещениям и деформациям выразим, как: 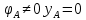 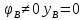 Для определения 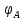 выразим выразим 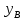 через условие метода начальных параметров (МНП): через условие метода начальных параметров (МНП):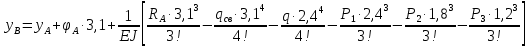 =0 =0Отсюда получим: 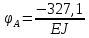  ( (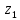 )= )=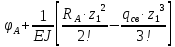 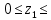 0,7м 0,7м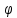 ( ( )= )=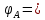 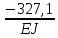 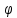 ( (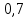 )= )=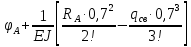 = =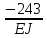 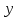 ( (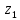 )= )=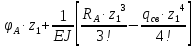  0,7м 0,7м ( ( )=0 )=0 ( (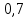 )= )=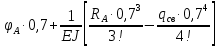 = =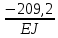 Сектор 2-2 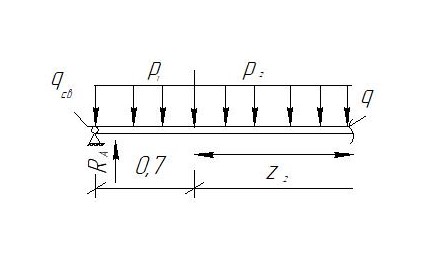 Q( 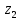 )= )=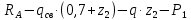 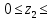 0,6м 0,6мQ(  )= )=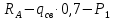 =181,5 кгс =181,5 кгсQ( 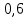 )= )=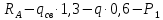 =99,9 кгс =99,9 кгсM( 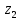 )= )=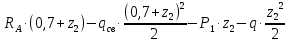 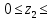 0,6м 0,6мM(  )= )=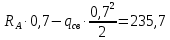 кгс кгс M(  )= )=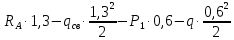 =320,1 кгс =320,1 кгс  ( ( )= )=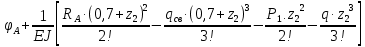  0,6м 0,6м ( ( )= )=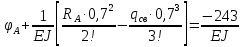 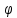 ( (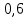 )= )=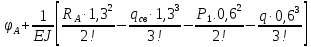 = =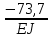 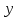 ( (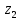 )= )=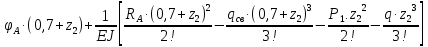 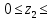 0,6м 0,6м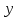 ( ( )= )=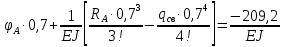 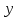 ( (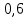 )= )=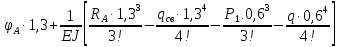 = =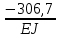 Сектор 3-3 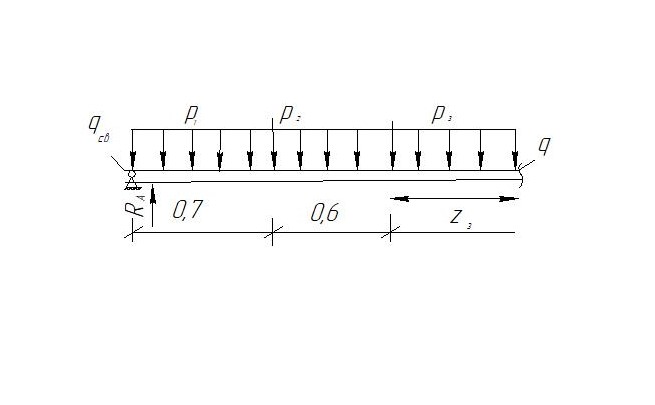 Q( 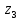 )= )=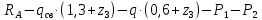 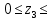 0,6 м 0,6 мQ(  )= )=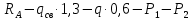 =7,9 кгс =7,9 кгсQ( 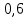 )= )=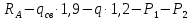 =-73,7 кгс =-73,7 кгсM( 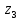 )= )=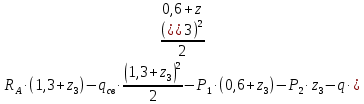 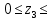 0,6м 0,6мM(  )= )=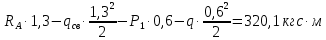 M( 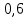 )= )=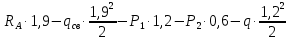 =300,4 кгс =300,4 кгс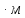 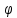 ( (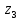 )= )=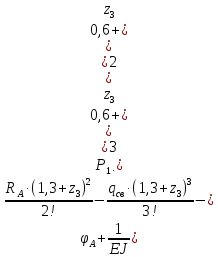  0,6м 0,6м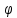 ( ( )= )=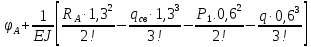 = =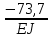 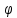 ( (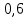 )= )=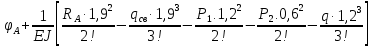 = =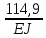 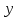 ( (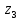 )= )=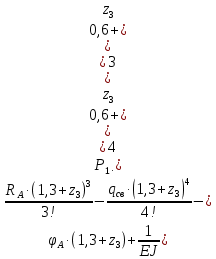 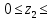 0,6м 0,6м ( ( )= )=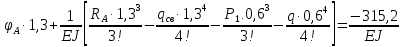  ( ( )= )=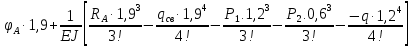 = =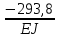 Сектор 4-4 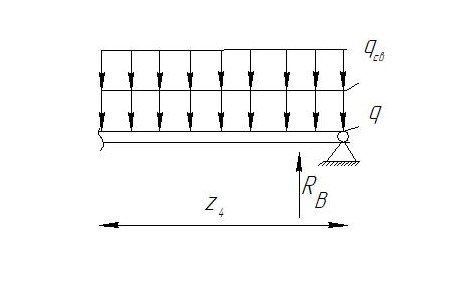 Q(  )= )=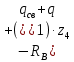 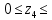 1,2м 1,2мQ(  )= )=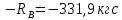 Q(  )= )=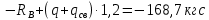 M( 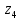 )= )=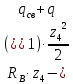 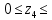 1,2м 1,2мM(  )= )=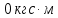 M( 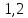 )= )=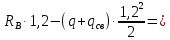 300,4 кгс 300,4 кгс  ( (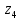 )= )=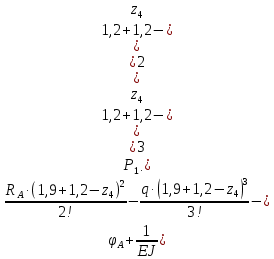 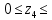 1,2 м 1,2 м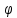 ( ( )= )=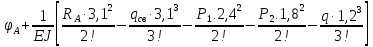 = =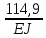 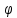 ( (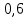 )= )=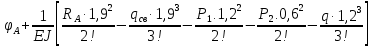 = =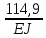 Так как мы получили значения прогибов на границах сектора 4-4,то можно перейти к построению эпюр. 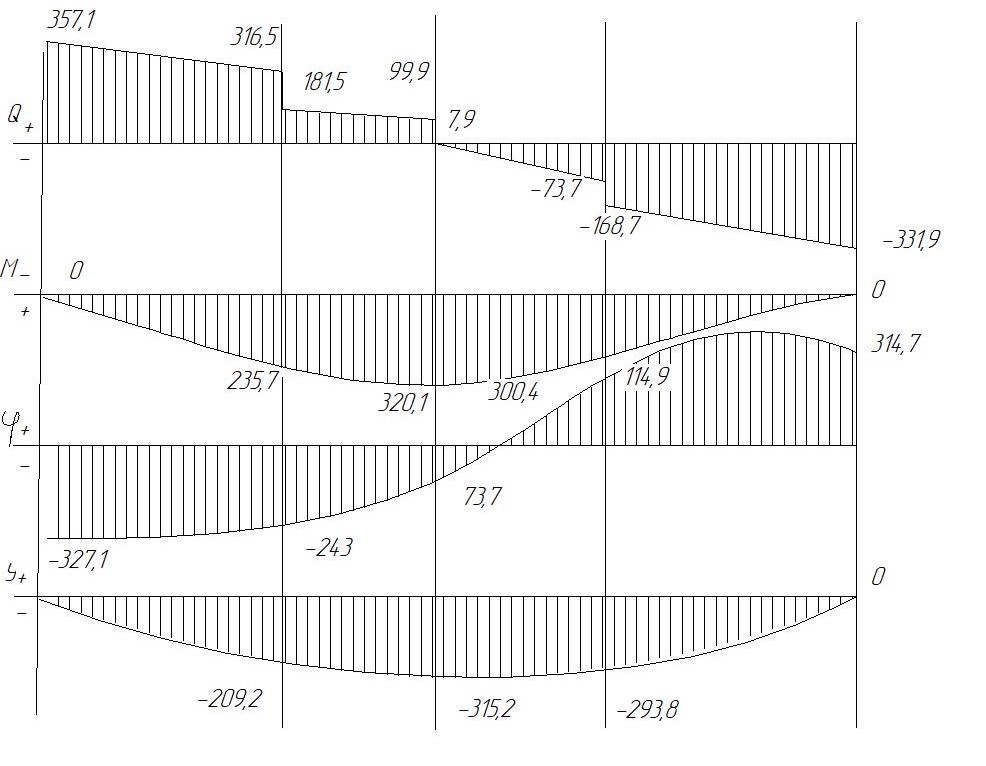 Задание №5 Для определения максимального прогиба необходимо найти аргумент 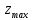 . Для этого воспользуемся равенством . Для этого воспользуемся равенством 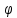 ( (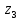 )=0, что является аналогичным условию: )=0, что является аналогичным условию: 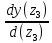 =0: =0: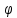 ( (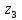 )= )=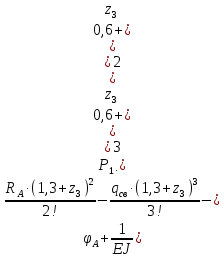 Решением кубического уравнения относительно 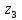 будет решение с положительным знаком: будет решение с положительным знаком: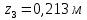 Деформация в этой точке для 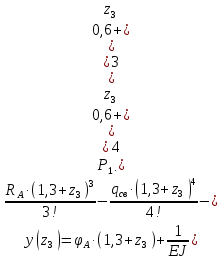 С учётом модуля упругости пихты и момента инерции для ПСК получим максимальный прогиб: 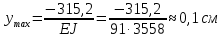 Допустимый прогиб для пихты: 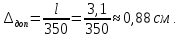 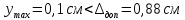 Таким образом: запас по жёсткости обеспечен. Задание №6 Функция зависимости момента инерции ПСК J( 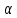 ) от угла наклона ) от угла наклона 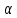 ПСК в плоскости ХОУ лежит в диапазоне её значений для ортогональных осей x и y. ПСК в плоскости ХОУ лежит в диапазоне её значений для ортогональных осей x и y.Так как отношение 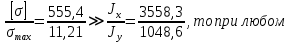 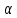 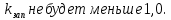 Заключение В курсовой работе мною был проведен расчет конструктивного элемента на нормативные и расчетные сочетания нагрузки в соответствии с исходными данными, приведенными в методическом приложении к курсовой. В задании 1 я определил центр тяжести сложного сечения применяя формулы статического момента площади, а также вычислил осевые моменты инерции, центробежный момент инерции и моменты сопротивления изгибу. В задании 2 я для расчетной схемы конструктивного элемента их исходных данных построил эпюры поперечных сил и изгибающих моментов, используя метод секторов. В задании 3 я провел аналогичный расчет, как и в задании 2, но уже с учетом коэффициентов надежности к нагрузкам и собственного веса конструктивного элемента. По вычисленному максимальному изгибающему моменту я проверил условие прочности с учетом запаса и установил, что запас обеспечен заведомо. В задании 4 я провел расчет в той же постановке, что и в задании 3, но уже в нормативном сочетании, так как это требуется при вычислении углов и прогибов конструктивного элемента в соответствии с 2 предельным состоянием. После построения уравнений внутренних усилий и перемещений, а также их эпюр, я перешел к заданию 5, в котором требовалось проверить условие жесткости конструктивного элемента. Для этого я сравнил максимальный прогиб конструкции, вычисленный из соображений равенства углового перемещения в этой точке нулю, и допустимый прогиб конструкции, определяемый для материала исходными данными, и установил, что жесткость заведомо обеспечивается большим запасом. В последнем задании я проверил возможность «истощения» запаса по прочности при поворачивании поперечного сечения конструкции (ПСК) перпендикулярно ее продольной оси и установила невозможность этого «истощения» ввиду заданных ПСК, нагрузок и пролета конструкции. Список литературы Беляев, Н.М. Сопротивление материалов / Н.М. Беляев. - М.: Альянс, 2015. - 608 c. Березина, Е.В. Сопротивление материалов: учебное пособие / Е.В. Березина. - М.: Альфа-М, 2017. - 416 c. Котляров, А.А. Теоретическая механика и сопротивление материалов: компьютерный практикум. / А.А. Котляров. - Рн/Д: Феникс, 2017. - 384 c. Кривошапко, С.Н. Сопротивление материалов. практикум.: Учебное пособие для прикладного бакалавриата / С.Н. Кривошапко, В.А. Копнов. - Люберцы: Юрайт, 2016. - 353 c. Кривошапко, С.Н. Сопротивление материалов: Учебник и практикум для прикладного бакалавриата / С.Н. Кривошапко. - Люберцы: Юрайт, 2016. - 413 c. Работнов, Ю.Н. Сопротивление материалов / Ю.Н. Работнов. - М.: Ленанд, 2019. - 456 c. Сидорин, С.Г. Сопротивление материалов: теория, тестовые.: Учебное пособие / С.Г. Сидорин, Ф.С. Хайруллин. - М.: Риор, 2017. - 352 c. Сидорин, С.Г. Сопротивление материалов. Пособие для решения контрольных работ студентов-заочников: Учебное пособие / С.Г. Сидорин. - СПб.: Лань, 2018. - 212 c. Шатохина, Л.П. Сопротивление материалов. Расчёты при сл.: Учебное пособие / Л.П. Шатохина, Е.М. Сигова, Я.Ю. Белозёрова и др. - М.: Инфра-М, 2018. - 455 c. | ||||||||||||||||||||||||||||
