признак. Самостоятельная работа по теме 1 признак равенства треугольников
 Скачать 122.54 Kb.
|
№1. Вариант 1. Контрольная работа №1. Вариант 2. 1)Три точки P, Q и R лежат на одной прямой. Известно, что PQ=16см,QR=28см. Каким может быть расстояние PR? 2)Сумма вертикальных углов, образованных при пересечении прямых a и b, равна 114°.Найдите все образовавшиеся углы. 3) С помощью транспортира начертите угол, равный 114°, и проведите биссектрису одного из смежных с ним углов. Контрольная работа №2. Вариант 1. 1)На рис.1 отрезки АВ и СД имеют общую середину О.Докажите, что< ДАО= <СВО. 2)Луч АД - биссектриса угла А.На сторонах угла А отмечены точки В и С так, что <АДВ=<АДС. Докажите, что АВ=АС. 3)Начертите равнобедренный треугольник АВС с основанием ВС. С помощью циркуля и линейки проведите медиану ВВ1 к боковой стороне АС. Вариант 2. 1)На рис. 2 отрезки МЕ и РК точкой Д делятся пополам. Докажите, что <КМД=<РЕД. 2)На сторонах угла Д отмечены точки М и К так, что ДМ=ДК. Точка Р лежит внутри угла Д и РК=РМ. Докажите, что луч ДР- биссектриса угла МДК. 3) Начертите равнобедренный треугольник АВС с основанием АС и острым углом В. С помощью циркуля и линейки проведите высоту из вершины угла А. 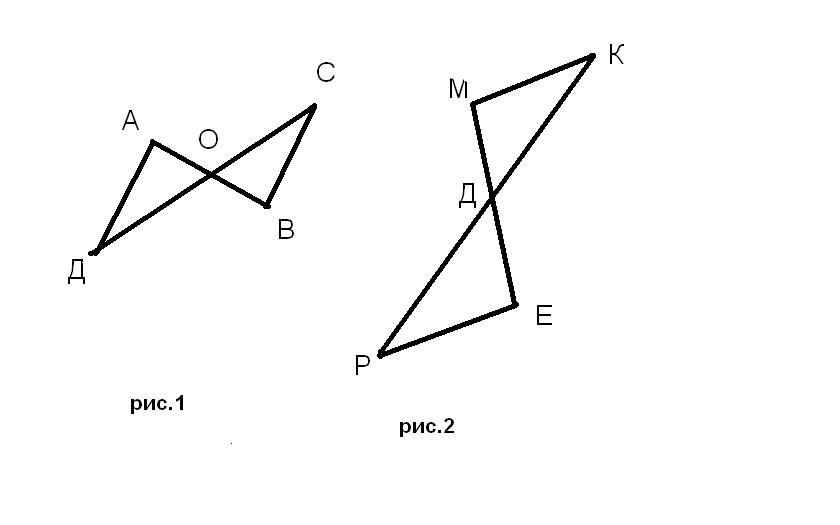 Контрольная работа №3. Вариант 1. 1)Отрезки ЕF и РД пересекаются в их середине М.Докажите, что РЕ II ДF. 2)Отрезок ДМ- биссектриса треугольника СДЕ. Через точку М проведена прямая, параллельная стороне СД и пересекающая сторону ДЕ в точке N.Найдите углы треугольника ДМN, если <СДЕ=68°. Контрольная работа №3. Вариант 2. Отрезки MN и EF пересекаются в их середине Р. Докажите, что EN II MF. Отрезок АД-биссектриса треугольника АВС. Через точку Д проведена прямая, параллельная стороне АВ и пересекающая сторону АС в точке F.Найдите углы треугольника АДF, если <ВАС=72°. Контрольная работа №4.  Вариант 1. 1)На рис.1 угол АВЕ равен 104°, угол ДСF равен 76°,АС=12 см.Найдите сторону АВ треугольника АВС. 2)В треугольнике СДЕ точка М лежит на стороне СЕ, причём угол СМД острый. Докажите, что ДЕ> ДМ. 3)Периметр равнобедренного тупоугольного треугольника равен 45 см, а одна из его сторон больше другой на 9 см. Найдите стороны треугольника. Вариант 2. 1)На рис.2 угол ВАЕ равен 112 °, угол ДВF равен 68° , ВС=9см.Найдите сторону АС треугольника АВС. 2)В треугольнике MNP точка К лежит на стороне МN, причём угол NКР острый. Докажите, что КР<МР. 3)Одна из сторон равнобедренного тупоугольного треугольника на 17см меньше другой. Найдите стороны этого треугольника, если его периметр равен 77см. Контрольная работа №5. Вариант 1. 1)В остроугольном треугольнике MNP биссектриса угла М пересекает высоту NК в точке О, причём ОК=9см.Найдите расстояние от точки О до прямой МN. 2)Постойте прямоугольный треугольник по гипотенузе и острому углу. Дополнительное задание. С помощью циркуля и линейки постройте угол равный 150°. Контрольная работа №5. Вариант 2. 1)В прямоугольном треугольнике ДСЕ с прямым углом С проведена биссектриса ЕF, причём FC=13cм.Найдите расстояние от точки F до прямой ДЕ. 2) Постойте прямоугольный треугольник по катету и прилежащему к нему острому углу. Дополнительное задание. С помощью циркуля и линейки постройте угол равный 105°. Вариант 2 1. BD=AC и BC = AD. Докажите, что ADB = ACB. 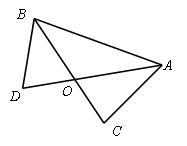 2. В MNK MN = NK, NC – медиана, MNK = 120°. Найдите MNC. 3. Периметр равнобедренного треугольника равен 13,6см. Его основание меньше боковой стороны на 2 см. Найдите стороны треугольника. 4. На сторонах угла А отмечены точки М и K так, что АМ = АK. Точка Р лежит внутри угла А и РK = РМ.Докажите, что луч АР – биссектриса угла МАK. |
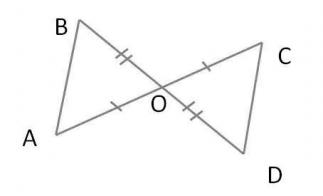
) Дано: ВО=ОD, AO=OС.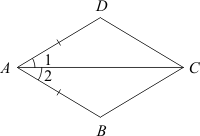 
) А)Докажите равенство треугольников ADC и ABC, 
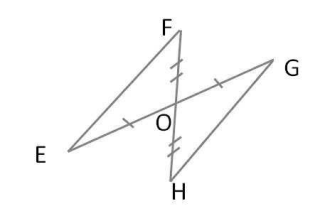) угол, противолежащий стороне МQ.
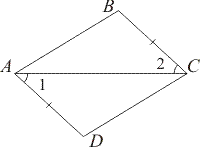) А) Докажите равенство треугольников ABC и СDА, изображенных на рисунке, если BC = AD и ∠1 = ∠2. 
) 
)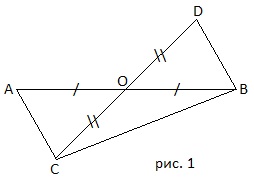