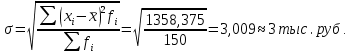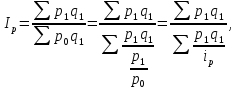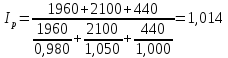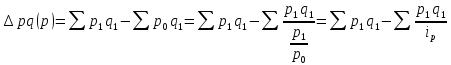|
|
практическое задание по статистике. статистика. Самсонова Алина Алексеевна
Практическое задание
дисциплине
Выполнил(а) студент(ка)
|
Самсонова Алина Алексеевна
|
|
фамилия имя отчество
|
Идентификационный номер:
|
2101-0700-2101411
|
|
|
|
|
|
|
|
|
|
|
|
|
Пермь 2023_
Задача 1.
Имеются следующие данные за год по заводам одной промышленной компании:
Завод
|
Среднее число рабочих, чел.
|
Основные фонды, млн руб.
|
Продукция, млн руб.
|
Завод
|
Среднее число рабочих, чел.
|
Основные фонды, млн руб.
|
Продукция, млн руб.
|
1
|
700
|
250
|
300
|
9
|
1 400
|
1 000
|
1 600
|
2
|
800
|
300
|
360
|
10
|
1 490
|
1 250
|
1 800
|
3
|
750
|
280
|
320
|
11
|
1 600
|
1 600
|
2 250
|
4
|
900
|
400
|
600
|
12
|
1 550
|
1 500
|
2 100
|
5
|
980
|
500
|
800
|
13
|
1 800
|
1 900
|
2 700
|
6
|
1 200
|
750
|
1 250
|
14
|
1 700
|
1 750
|
2 500
|
7
|
1 100
|
700
|
1 000
|
15
|
1 900
|
2 100
|
3 000
|
8
|
1 300
|
900
|
1 500
|
|
|
|
|
На основании приведенных данных составьте групповую таблицу зависимости выработки на одного рабочего от величины заводов по числу рабочих. Число групп – три
Решение:
Выработка на одного работающего количества произведенной продукции: В=К/(Ч)
Выработка для каждого завода:
Завод
|
Среднее число рабочих, чел.
|
Основные фонды, млн руб.
|
Продукция, млн руб.
|
Выработка на одного работающего
|
1
|
700
|
250
|
300
|
0,43
|
2
|
800
|
300
|
360
|
0,45
|
3
|
750
|
280
|
320
|
0,43
|
4
|
900
|
400
|
600
|
0,67
|
5
|
980
|
500
|
800
|
0,82
|
6
|
1200
|
750
|
1250
|
1,04
|
7
|
1100
|
700
|
1000
|
0,91
|
8
|
1300
|
900
|
1500
|
1,15
|
9
|
1400
|
1000
|
1600
|
1,14
|
10
|
1490
|
1250
|
1800
|
1,21
|
11
|
1600
|
1600
|
2250
|
1,41
|
12
|
1550
|
1500
|
2100
|
1,35
|
13
|
1800
|
1900
|
2700
|
1,50
|
14
|
1700
|
1750
|
2500
|
1,47
|
15
|
1900
|
2100
|
3000
|
1,58
|
Величина интервала: i=(Xmax-Xmin)/( n) , где X max и X min – максимальное и минимальное значения признака т.е. число рабочих, а n – число групп.
i=(1900-700)/( 3)=400 - получили 3 группы: 1гр. - от 700 до 1100 рабочих
2 гр. – от 1100 до 1500 рабочих 3 гр. – от1500 до 1900 рабочих
Рабочая таблица:
Номер групп ы
|
Номера заводов
|
Среднее число рабочих, чел.
|
Основные фонды, млн руб
|
Продукция
, млн руб.
|
Выработка на одного рабочего
|
1.
|
1
|
700
|
250
|
300
|
0,43
|
|
3
|
750
|
280
|
320
|
0,43
|
|
2
|
800
|
300
|
360
|
0,45
|
|
4
|
900
|
400
|
600
|
0,67
|
|
5
|
980
|
500
|
800
|
0,82
|
|
7
|
1100
|
700
|
1000
|
0,91
|
ИТОГО 6 2430 3380 3,70
|
2.
|
6
|
1200
|
750
|
1250
|
1,04
|
|
8
|
1300
|
900
|
1500
|
1,15
|
|
9
|
1400
|
1000
|
1600
|
1,14
|
|
10
|
1490
|
1250
|
1800
|
1,21
|
ИТОГО 4 3900 6150 4,55
|
3.
|
12
|
1550
|
1500
|
2100
|
1,35
|
|
11
|
1600
|
1600
|
2250
|
1,41
|
|
14
|
1700
|
1750
|
2500
|
1,47
|
|
13
|
1800
|
1900
|
2700
|
1,50
|
|
15
|
1900
|
2100
|
3000
|
1,58
|
ИТОГО 5 8850 8200 4,55
|
По данным рабочей таблицы составляем аналитическую группировку:
Номер группы
|
Количество заводов
|
Группы заводов по числу рабочих
|
Основные фонды в среднем на один завод, млн руб.
|
Продукция в среднем на один завод, млн руб.
|
Выработка на одного рабочего в среднем на один завод
|
1
|
6
|
700-1100
|
405
|
563,33
|
0,62
|
2
|
4
|
1100-1500
|
975
|
1537,50
|
1,14
|
3
|
5
|
1500-1900
|
1770
|
2510
|
1,46
|
Вывод: С увеличением количества рабочих увеличиваются основные фонды и выработка на одного рабочего.
3адача 2. Выпуск продукции на заводе в 2020 г. составил 160 млн руб. По плану на 2021 г. предусматривалось выпустить продукции на 168 млн руб., фактически же выпуск составил 171,36 млн руб. Вычислите относительные величины планового задания и выполнения плана.
Решение.
На основе имеющихся данных рассчитаем относительные показатели: — относительная величина планового задания: ОВПЗ = ВП1пл : ВП0ф * 100% = 168 : 160 * 100% = 105% — относительная величина выполнения плана: ОВВП = ВП1ф : ВП1пл * 100% = 171,36 : 168 * 100% = 102%
Вывод: в 2021 году планировалось увеличить объем производства продукции на 5% по сравнению с 2020 г., по итогам года план производства продукции был перевыполнен на 2%.
Задача 3. На основании данных, представленных в таблице, определите установленную среднюю продолжительность трудового дня производственного рабочего по заводу в целом:
Показатель
|
1 цех
|
2 цех
|
3 цех
|
4 цех
|
Количество смен
|
3
|
3
|
2
|
1
|
Число рабочих в смену
|
600
|
800
|
400
|
200
|
Продолжительность смены
|
8
|
8
|
8
|
6
|
Решение: Для начала узнаем количество работников в цеху: Цех 1 – 600*3=1800
Цех 2 – 800*3=2400 Цех 3 – 400*2=800 Цех 4 – 200*1=200
Количество работников на заводе: Цех 1+ Цех 2 + Цех 3 + Цех 4 1800 + 2400 + 800 + 200
= 5200
Количество работников работающих по 8 часов: 1800 + 2400 + 800 = 5000 (96,2%)
Количество работников работающих по 6 часов: 200 (3,2%)
Средняя продолжительность смены: 8*96,2%+6*3,2% = 7,696+0,192=7,888 часа.
Ответ: средняя продолжительность смены 7,888 часа.
Задача 4.
|
Имеются следующие данные о распределении рабочих цеха по размеру месячной заработной платы:
Размер зарплаты, тыс. руб.
|
до 5,0
|
5,0-7,5
|
7,5-10,0
|
10,0-12,5
|
свыше 12,5
|
Число рабочих, чел.
|
15
|
15
|
25
|
65
|
30
|
Определите среднюю месячную зарплату рабочих цеха, моду и медиану, среднеквадратическое отклонение и коэффициент вариации.
Решение
Среднюю месячную зарплату рабочих цеха определяем по формуле средней арифметической взвешенной:
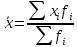
- середины интервалов (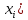 , тыс. руб. , тыс. руб.
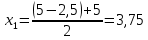
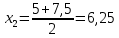
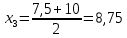
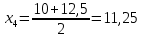
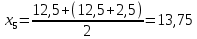
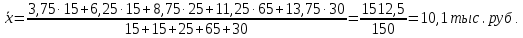
Мода
Модальный интервал определяем по наибольшему числу рабочих (65):
10,0–12,5
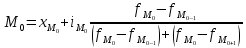
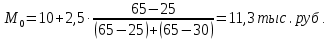
Медиана
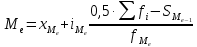
№ группы
|
Размер зарплаты
(тыс. руб.)
|
Число рабочих
(частота)
(fі)
|
Накопленная частота
(Si)
|
|
До 5
|
15
|
15
|
|
5,0–7,5
|
15
|
30
|
|
7,5–10,0
|
25
|
55
|
|
10,0–12,5
|
65
|
120
|
|
свыше 12,5
|
30
|
150
|
Всего
|
150
|
|
Медианный интервал:
10,0–12,5 накопленная частота 120>75 (150/2)
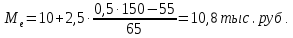
Среднее квадратическое отклонение
№ группы
|
Размер зарплаты
(тыс. руб.)
|
Середины интервалов
(xі)
|
Число рабочих
(частота)
(fі)
|
(xi - 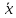 )2fi )2fi
|
|
До 5
|
3,75
|
15
|
(3,75 -10,1)2·15 = 604,8375
|
|
5,0–7,5
|
6,25
|
15
|
(6,25 -10,1)2·15 = 222,3375
|
|
7,5–10,0
|
8,75
|
25
|
(8,75 -10,1)2·25 = 45,5625
|
|
10,0–12,5
|
11,25
|
65
|
(11,25 -10,1)2·65 = 85,9625
|
|
свыше 12,5
|
13,75
|
30
|
(13,75 -10,1)2·30 = 399,675
|
Всего
|
-
|
150
|
1358,375
|
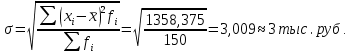
Коэффициент вариации
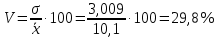
Выводы. Средняя месячная зарплата рабочих цеха 10,1 тыс. руб. Наиболее распространенная зарплата 11,3 тыс. руб. (мода). Приблизительно у половины рабочих размер зарплаты меньше 10,8 тыс. руб., у второй половины – больше указанной суммы (медиана). Размер зарплаты по группам рабочих отклоняется от среднего по цеху в ту или иную сторону на 3 тыс. руб. (среднее квадратическое отклонение) или на 29,8% (коэффициент вариации). Коэффициент вариации меньше 33%, поэтому можно утверждать, что совокупность однородная.
Задача 5
Объем продукции на промышленном предприятии повысился в 2016 году по сравнению
с 2011 годом на 100 млн рублей в сопоставимых ценах, или на 25 %.
В 2021 году объем продукции увеличился по сравнению с 2016 годом на 20 %.
Определите:
1) объем выпуска продукции предприятия в 2011, 2016, 2021 годах;
2) среднегодовые темпы прироста выпуска продукции за:
а) 2011-2021 гг.; б) 2016-2021 гг.; в) 2011-2016гг.
Решение:
1.В период с 2011 по 2016 годы имеет рост объема продукции на 100 млн. рублей или
на 25%. Таким образом, если объем производства в 2011 года составлял X2011, то получаем:
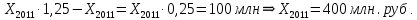
Объем производства в 2016 году равен:
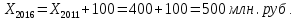
В 2021 году объем продукции увеличился по сравнению с 2016 годом на 20 % и составил:
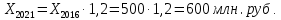
2.а) Общий темп роста в период с 2011 по 2021 год составил:
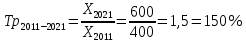
Среднегодовой темп роста в период с 2011 по 2021 год составил:
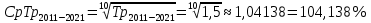
Среднегодовой темп прироста в период с 2011 по 2021 год составил:
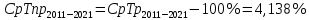
б) Общий темп роста в период с 2016 по 2021 год составил:
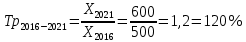
Среднегодовой темп роста в период с 2016 по 2021 год составил:
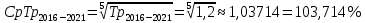
Среднегодовой темп прироста в период с 2016 по 2021 год составил:
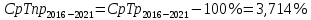
в) Общий темп роста в период с 2011 по 2016 год составил:
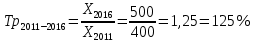
Среднегодовой темп роста в период с 2011 по 2016 год составил:
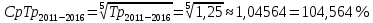
Среднегодовой темп прироста в период с 2011 по 2016 год составил:
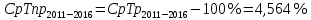
Ответ:
Объем выпуска продукции предприятия в 2011году равен 400 млн. руб., в 2016 году равен
500 млн. руб., в 2021 году объем продукции увеличился по сравнению с 2016 годом на 20 %
и составил 600 млн. руб. Среднегодовые темпы прироста выпуска продукции
в период с 2011 по 2021 год составил 4,138%, в период с 2016 по 2021 год составил 3,714%,
в период с 2016 по 2021 год составил 4,564%.
Задача 6. По одному из предприятий промышленности стройматериалов имеются
следующие данные:
Виды продукции
|
Снижение (–) или повышение (+) оптовых цен в отчетном периоде по сравнению с базисным (в %)
|
Реализовано продукции в отчетном периоде (тыс. руб.)
|
Строительные блоки
|
–2
|
1 960
|
Панели
|
+5
|
2 100
|
Строительные детали
|
без изменения
|
440
|
Определите общий индекс цен и сумму роста или снижения объема реализации продукции
за счет изменения цен.
Найдем индивидуальные индексы цен.
Строительные блоки:
ip = (100% - 2%) / 100% = 0,980
Панели:
ip = (100% + 5%) / 100% = 1,050
Строительные детали:
ip = (100% + 0%) / 100% = 1,000
Общий индекс цен
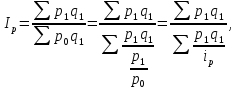
где p – цены, q – физический объем, pq – объем реализации продукции, индексом 0
обозначены данные базисного периода, индексом 1 – данные отчетного периода.
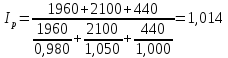
Сумма роста объема реализации продукции за счет изменения цен
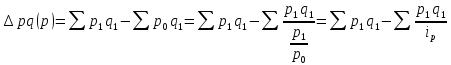
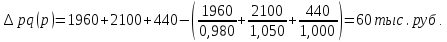
Общий индекс цен:
Ig= 100 – 2 = 98% = 0.98
Ig = 100+5 = 105% = 1.05
I = p1g1|ig*p0g0
1960+2100+440/0.98*1960 +1.05*2100+1*440 = 4500/1920.8+2205+440 = 0.986 = 98.6
Ответ: общий индекс цен и сумму роста или снижения объема реализации продукции
за счет изменения цен составляет 98.6
|
| |
|
|
 Скачать 102.53 Kb.
Скачать 102.53 Kb.