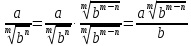матем сауаттылық тест. Математикалық сауаттылыққа тест тапсырмалары (1) — копия. Сандар тізбегі Сандар тізбегі
 Скачать 2.88 Mb. Скачать 2.88 Mb.
|
|
Түбір көрсеткіш басқа болса, формула былай болады:
3-МЫСАЛ. Бөлшектің бөліміндегі иррационалдықтан құтылыңыз: 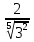 А) 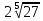 В) В) 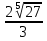 С) С) 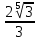 Д) Д) 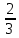 E) E) 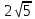 Шешуі : Бөлшектің алымын да, бөлімін де 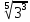 -ге көбейтеміз: -ге көбейтеміз: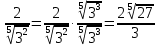 Жауабы : В) Жауабы : В) 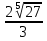 Бөлшектің бөлімінде қосу-азайту болса, формулалар былай болады:  Бөлшектің бөлімінде үш дәрежелі түбір қосу-азайтумен болса, формулалар былай болады:  Радикал ішіндегі радикалды түрлендірі:  Калькуляторды қолданбай түбір астындағы натурал санды табу Көптеген адамдар түбірдің астындағы санның мәнін табуға қиналады да дереу калькуляторға жүгінеді. Бірақ сынақтарда, емтихандарда, ҰБТ – да калькуляторды қолдануға тыйым салынғанын біз білеміз. Сондықтан калькуляторды қолданбай түбірдің астындағы натурал санды табуды үйренуіміз керек. 1-МЫСАЛ: 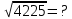 Өрнегінің мәнін табыңыз. Өрнегінің мәнін табыңыз.А ) 45 В) 75 С) 55 Д) 35 E) 65 Шешуі : Оны табу үшін біз 1) Соңынан санағанда екінші санды сызып тастаймыз: Сонда бізде екі бөлік қалды 42 жоне 5. 2) Бірінші бөлігі қай санның квадратына жақын? 72 = 49 => 7 бола алмайды. Себебі 49 саны 42-ден асып кетгі. 42-ден аспауы керек. 62 = 36 => 6 болады. Себебі 6 санының квадраты 42-ге ең жақын сан. Сонымен алғашкы бөлігі 6.  3)Екінші бөлігін табу үшін “0-бен 9-ға дейінгі қай санның квадратын соңғы цифрымен сәйкес келеді?” деген сұраққа жауап береміз. 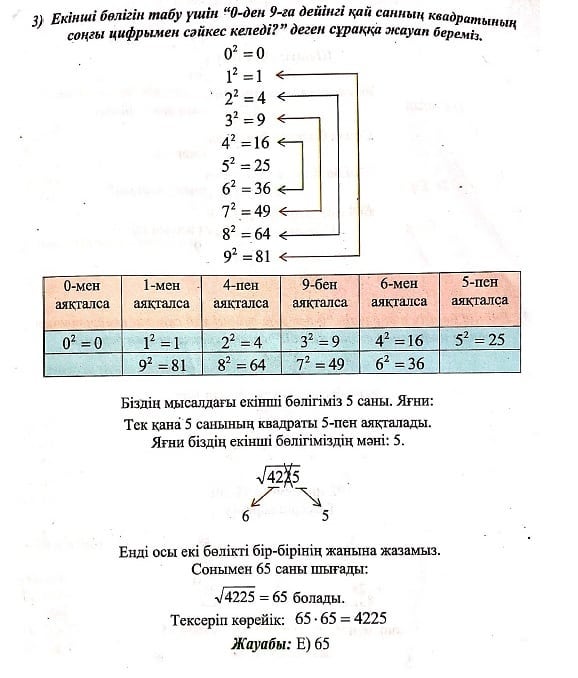
Біздің мысалдағы екінші бөлігіміз 5 саны. Яғни: Тек қана 5 санының квадраты 5-пен аяқталады. Яғни біздің екінші бөлігіміздің мәні: 5.  Енді осы екі бөлікті бір-бірінің жанына жазамыз. Сонымен 65 саны шығады: 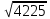 = 65 болады. = 65 болады.Тексеріп көрейік: 65 • 65 = 4225 Жауабы: Е) 65 Сағат, Күн, апта, айлар Біздің күнделікті өміріміз уақытпен тығыз байланысты. Уақыттың өлшем бірліктеріне тоқталайық: 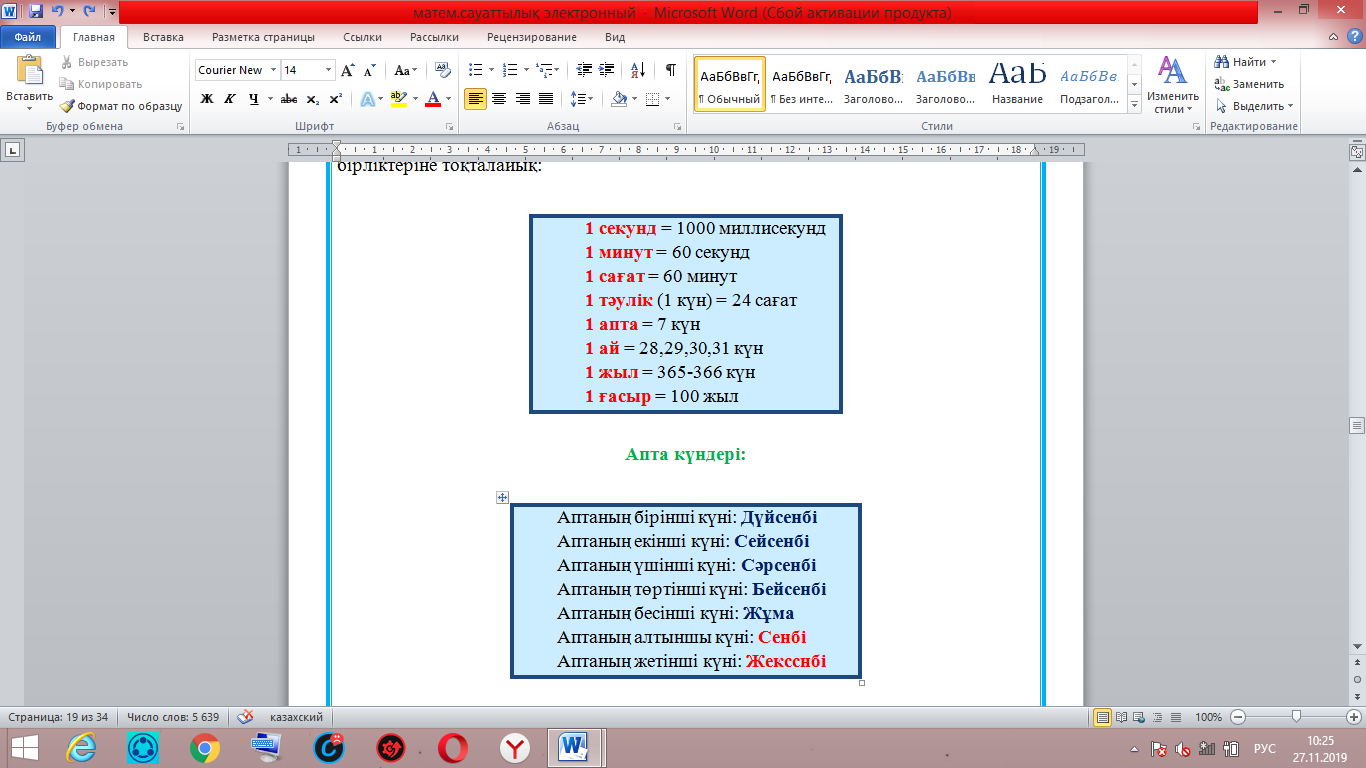 Апта күндері: 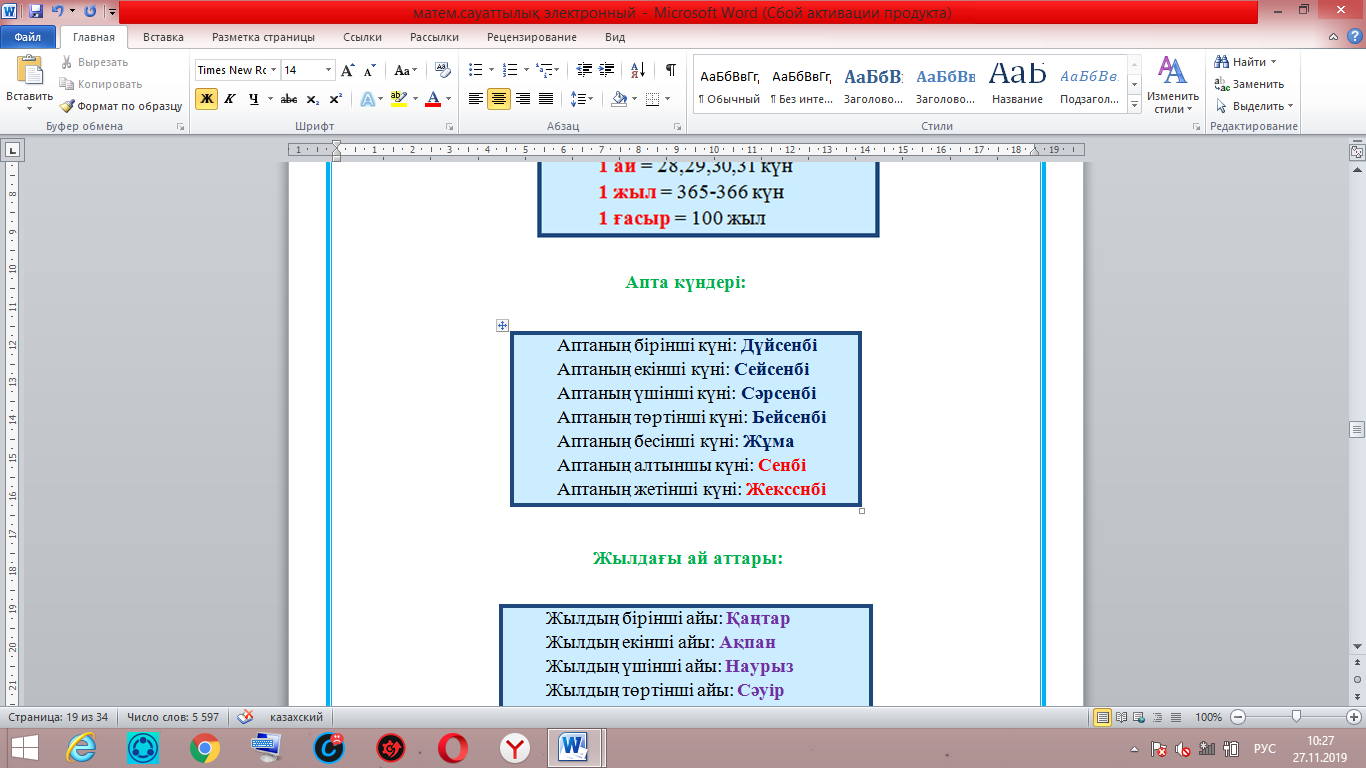 Жылдағы ай аттары: 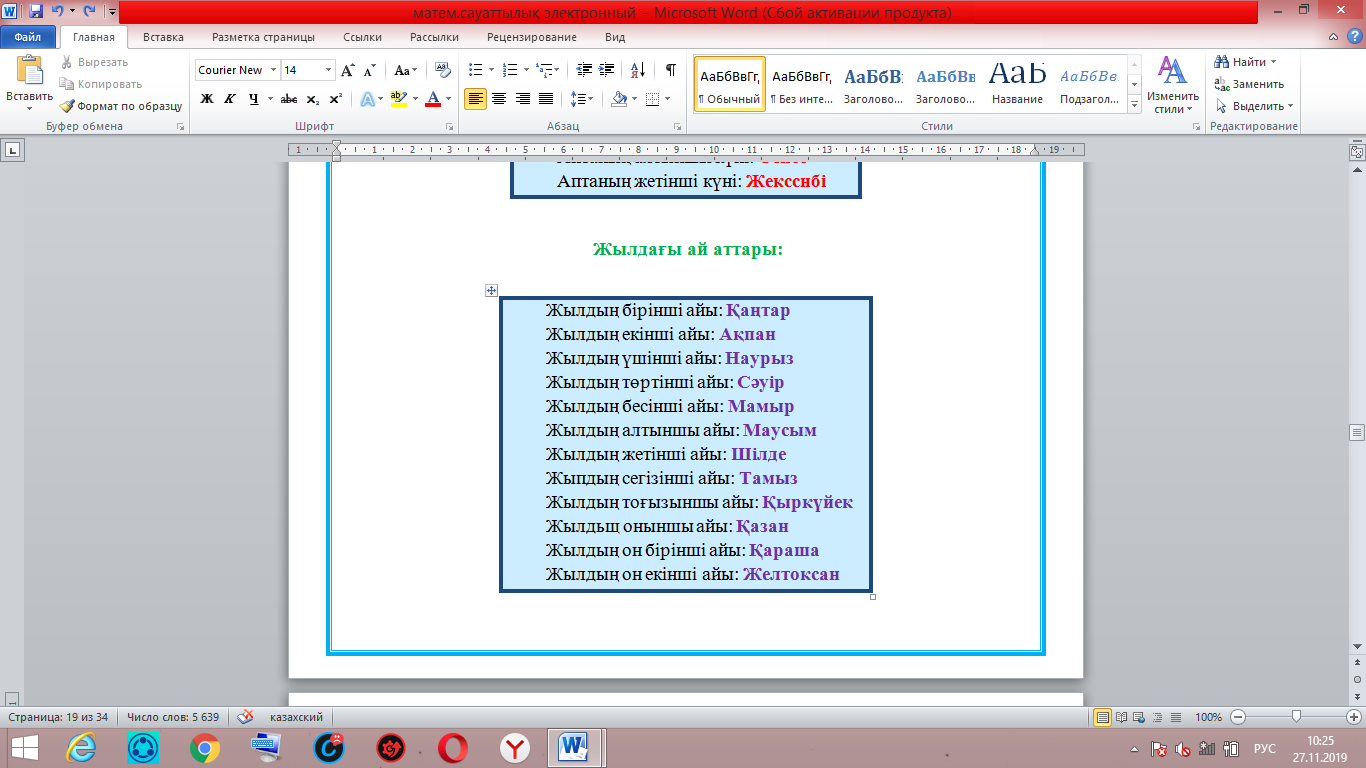 Айлардың неше күнге толатыны туралы мәлімет: 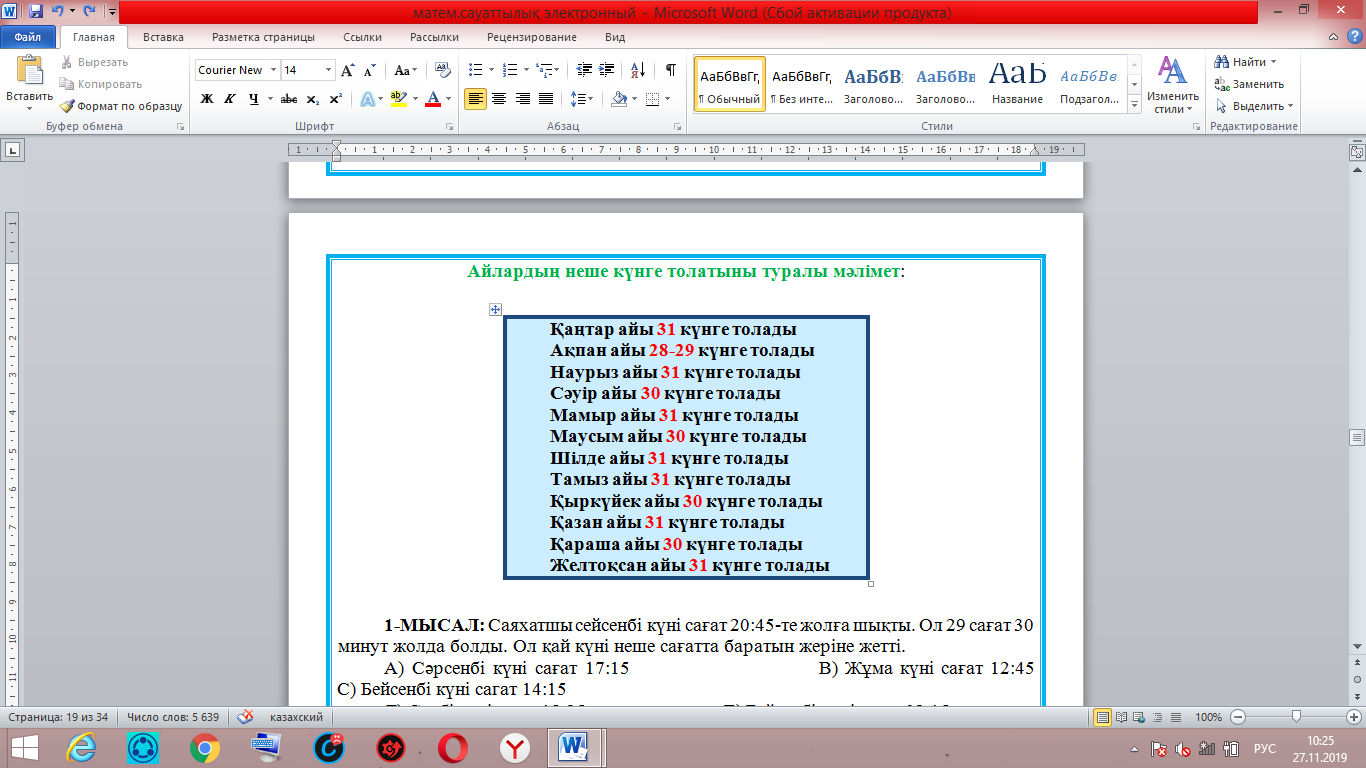 1-МЫСАЛ: Саяхатшы сейсенбі күні сағат 20:45-те жолға шықты. Ол 29 сағат 30 минут жолда болды.Ол қай күні неше сағатта баратын жеріне жетті. А) Сәрсенбі күні сағат 17:15 В) Жұма күні сағат 12:45 С) Бейсенбі күні сагат 14:15 Д) Сенбі күні сағат 18:25 Е) Бейсснбі күні сағат 02:15 Шешуі:Сейсенбі күні сағат 20:45-те жолға шыкты. Ол 29 сағат 30 минут жолда болды. Жауабы: Е) Бейсенбі күні сағат 02:15  2-МЫСАЛ: Бүгін аптаның сәрсенбі күні болса,100 күннен кейін аптаның қай күні болатынын табыңыз. А) Сәрсенбі күні В) Жұма күні С) Бейсенбі күні Д) Сенбі күні Е) Дүйсенбі күні Шешуі:Әр жеті күн сайын аптаның дәл сол күніне айналып келеді. Яғни 100-ді 7-ге бөлеміз де калдықты санаймыз. 100:7 = 14 (2 қалдық) Яғни 100 күнде 14 апта және 2 күн бар. 14 аптадан кейін қайтадан сәрсенбі күні боладыжәне 2 күн алдыға жүреміз: бейсенбі, жұма.Сонымен бүгін аптаның сәрсенбі күні болса,100 күннен кейін аптаның жұма күні болады. Жауабы: В) Жұма күні 3-МЫСАЛ: Бүгін тамыз айының 27-сі болса, 6 күпнен кейін қай айдың қай күні болатынын табыңыз. А) қыркүйек айының 3-і В) қыркүйек айының 7-сі С) қыркүйек айының 4-і Д) қыркүйек айының 2-сі Е) қыркүйек айының 1-і Шешуі:Тамыз айы 31 күнге толады.Сонымсн 4 күннен соң тамыз айы аяқталады.Тағы да 2 күн келесі айға өтеді.Яғни қыркүйек айының 2-сі болады. Жауабы: Д) қыркүйек айының 2-сі Өлшем бірліктер. Масштаб Өлшем- заттың, дененің сапалық және сандық сипаттарын көрсететін заңдылық.Ал өлшемнің бірліктеріне келетін болсақ, олар күнделікті тұрмыста, техникада, медицинада, шаруашылықтарда және т.б. ғылым салаларында кездеседі.Біз математикада күнделікті өмірде көп кездесетін өлшем бірліктерді қарастыратын боламыз.Егер өлшем бірліктер болмаса біз заттарды, денелерді салыстыра алмас едік, сол үшін өлшем бірліктерді білу өміріміздегі маңызды зандылықтардың бірі болмақ. ҰЗЫНДЫҚ ӨЛШЕМІ Ұзындық өлшемдері- күнделікті тіршілікте, ғылым салаларында көптеген денелердің, заттардың бойын, ұзындығын өлшеуге қолданылады.  АУДАН ӨЛШЕМІ Аудан өлшемдері- күнделікті тіршілікте, ғылым салаларында қандайда бір жазықтықтың, беттің, пішіннің алып жатқан аумағын, жерін өлшеуге қолданылады.  КӨЛЕМ ӨЛШЕМІ Көлсм өлшсмдсрі- күндслікті тіршілікте, ғылым салаларында қандай да бір геометриялық денелердіңкеңістікте алып жатқан бөлігін өлшеуге қолданылады.  САЛМАҚ ӨЛШЕМІ Салмақ өлшсмдсрі- күнделікті тіршілікте, ғылым салаларында қандай да бір денелердің массасын, салмағын өлшеуге қолданылады.  УАҚЫТ ӨЛШЕМІ Уақыт өлшсмдері- күнделікті тіршілікте, ғылым салаларында қандай да бір уақыт мезетін өлшеуге қолданылады.Уакыттың өлшем бірліктеріне тоқталайық:  Енді осы өлшемдерге бірнеше мысал есептер қарастырып көрейік. 1-МЫСАЛ.Адам демімен бірге тәулігіне 400 л көмірқышқыл газын шығарады.1 м 3 көмірқышқыл газының массасы 1,98 кг.Адам демімен тәулігіне неше килограмм көмірқышқыл газын шығарады ? А) 0,892 кг В) 0,728 кг С) 0,792 кг Д) 0,879 кг Е) 0,839 кг Шешуі:Бұл есепте жоғарыда айтып кеткендей 1 л = 1 дм3 екенін ескеріп осыдан 400 л = 400 дм3 екенін аламыз.1 м3 =1,98 кг екені белгілі, сонда 1000 дм3 =1,98 кг тең болады.Енді біз 400 дм3 көмірқышқыл газы қанша килограммға тең екенін табу үшін келесі пропорцияны құрамыз: 1000 дм3 ‒‒‒ 1,98 кг 400 дм3 ‒‒‒ х кг  400 дм3 * 1,98 кг 1000 дм3  = 0,792 кг Осыдан х-ті табатын болсақ: Сонда адам тәулігіне 0,792 кг көмірқышқыл газын шығаратынын таптық. Жауабы: С) 0,792 кг 2-МЫСАЛ.1 кг ауаның массасы 1,3 кг. Бөлменің өлшемдері: 7,5 м; 5,4 м; 3,2 м. Бөлме ішіндегі ауаның массасын табыңыз. А) 157,43 кг В) 168,48 кг С) 137,45 кг Д) 165,41 кг Е) 156,49 кг Шешуі: Ең алдымен бөлменің көлемін табамыз. Ол үшін үш өлшемді көбейтеміз:V = 7,5• 5,4•3,2 = 129,6 м 3 тең болады. Енді осындай көлемді бөлменің ішінде қанша килограмм ауа бар екенін табу үшін келесі пропорциядан х-ті табамыз. 129,6 м3—‒ х кг 1 м3 ‒‒‒ 1,3 кг  = 168,48 кг 129,6 м3 * 1,3 кг 1 м3 Жауабы: В) 168,48кг 3-МЫСАЛ. 3 м соқа тіркелген трактордың жылдамдығы 9 км/сағ болса, ол 5 сағатта қанша жер жыртатынын анықтаңыз. А) 15 га В) 14,5 га С) 13 га Д) 14 га Е) 13,5 га Шешуі: Суретін салып көрейік:  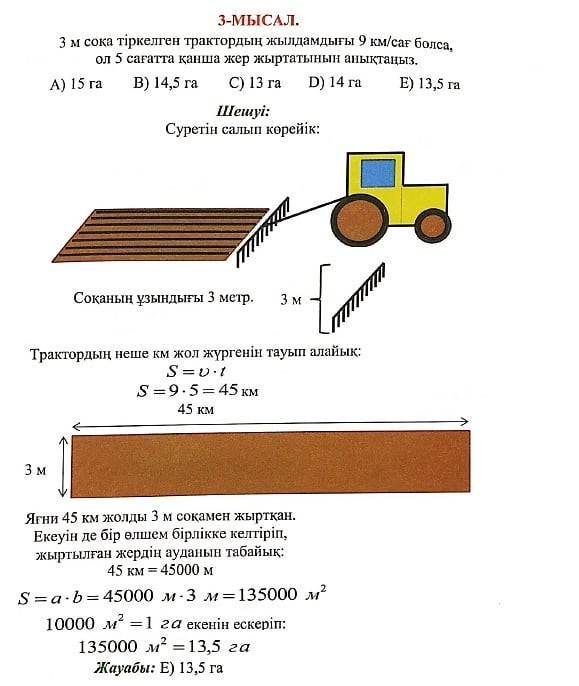 Трактордың неше км жол жүргенін тауып алайық: S = V • t S = 9•5 = 45 км Яғни 45 км жолды 3 м соқамен жыртқан. Екеуін де бір өлшем бірлікке келтіріп, жыртылған жердін ауданын табайық: 45 км = 45000 м S = a•b = 45000 м • 3 м = 135000 м2 10000 м2 = 1 га екенін ескеріп: 135000 м2 = 13,5 га Жауабы: Е) 13,5 га МАСШТАБ Масштаб - сызба, жоспардагы аэрофото түсірудегі немесе картадағы кесінді ұзындығының сол кесіндінің нақты ұзындығына қатынасы. Дерексіз санмен өрнектелген бұл қатынас сандық масштаб деп аталады. Жоспар мен карталардың сандық масштабы бөлшек сан арқылы өрнектеледі, алымы бірге тең болса, бөлімі бейнеленген сызықтын неше есе кішірейтілгенін керсетеді. Сонда масштаб - картадағы кескін ұзындығының, жер бетіндегі (шын өмірдегі) қашықтыкқа қатынасы.  1-МЫСАЛ. Масштабы 1:500 000 болатын картада екі қаланың арасы 4,5 см болса,олардың мекендегі (шын мәніндегі) арақашықтыгын табыңыз. А) 20,5 км В) 22,5 км С) 24,5 км Д) 23,5 км Е) 21,5 км Шешуі: Формула бойынша: 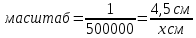 х=4,5 • 500000 х = 2250000 см = 22500 м = 22,5 км х = 22,5 км Сонда екі қаланың ара қашықтығы 22,5 км. Жауабы: В) 22,5 км 2-МЫСАЛ.Масштабы 1:2 000 000 болатын картада екі елді мекеннің арасы 5 см .Осы елді мекеннің жердегі арақашықтығын табыңыз. А) 115 км В) 110 км С) 124 км Д) 100 км Е) 215 км Шешуі: Формула бойынша: 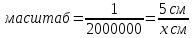 х= 5 • 2000000 х = 10000000 см = 100000 м = 100 км х = 100 км Сонда екі елді мекеннің шын мәніндегі, жердегі арақашықтығы 100 км-ге тең. Жауабы: Д) 100 км Эйлер-Венн диаграммасы Эйлер диаграммасы (Эйлер шеңберлері) — бұл жиындар арасындағықатынасты, геометриялық схемалар аркылы көрсету үшін пайдаланылатын диаграммалар.Ең алғаш оны Леонардо Эйлер қолданысқа енгізген болатын, ал оны ары қарай дамытып алгебра және логикалық есептерді шығаруға өз кітабында қолданған Джон Венн болатын.Сол себепті қазіргі танда бұл диаграммалар Эйлер-Венн диаграммасы болып қалыптасып, көптеген салаларда пайдаланылады, мысалы: математикада, логикада, менеджментге және т.б. қолданбалы бағыттарда пайдаланылады. Біз болсақ бұл диаграммаларды логикалық және алгебралық есептерді шығаруға, түсінуге пайдаланатын боламыз.Ал ендеше бұл теорияны түсіну үшін жиындарды қарастырайық.Кез келген А және В жиындары берілсін. А жиыннының элемснттерің А {1,2,3,4,5,6,7} болсын, ал В жиынынын элементгері В{1,3,5,7,9,11} болсын делік. Енді осы жиындарды пайдаланып Эйлер - Венн диаграммасын сызып көрелік. 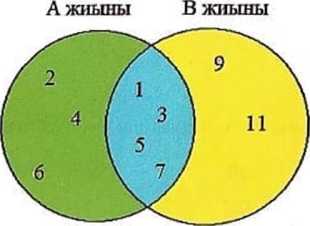 Енді осы жиындарға амалдар қолданып көрелік. БІРІГУ АМАЛЫ (ҚОСЫНДЫСЫ). А мен В жиындарының бірігуі деп - осы жиындардың барлық элементтерінен тұратын үшінші жиынды айтады.Оны А 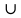 В арқылы белгілейді. Сонда екі жиынның бірігуін (қосынды) табу үшін екі жиынға да тиісті элементерді теріп жазамыз (диаграммадағы жасыл, сары және көк түстегі бөліктердегі сандар):А В арқылы белгілейді. Сонда екі жиынның бірігуін (қосынды) табу үшін екі жиынға да тиісті элементерді теріп жазамыз (диаграммадағы жасыл, сары және көк түстегі бөліктердегі сандар):А В {1,2,3,4,5,6,7,9,11} деген жаңа жиынды аламыз. В {1,2,3,4,5,6,7,9,11} деген жаңа жиынды аламыз.ҚИЫЛЫСУ АМАЛЫ. А мен В жиындарының қиылысуы деп осы жиындардың ортақ элементтерінен тұратын үшінші жиынды айтады. Оны А 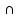 В арқылы белгілейміз. Сонда тек екі жиынға да ортақ элементтерді теріп жазамыз (диаграммадағы тек көк түсті бөліктегі сандар): А В арқылы белгілейміз. Сонда тек екі жиынға да ортақ элементтерді теріп жазамыз (диаграммадағы тек көк түсті бөліктегі сандар): А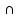 В {1,3,5,7} деген жаңа жиынды аламыз. В {1,3,5,7} деген жаңа жиынды аламыз.АЛУ АМАЛЫ (АЙЫРМАСЫ). А мен В жиындарының айырмасы деп А жиынының В жиынында болмайтын (В-ға тиісті емес) элементтерінен тұратын үшінші жиынды айтады. Оны А\В деп белгілейді. Сонда тек А жиынынатиісті, В жиынында жоқ сандарды теріп жазамыз (диаграммадағы тек жасыл түсті бөліктегі сандар): А\В {2,4,6} деген үшінші жиын аламыз.Осы жоғарыда көрсетілген Эйлер - Венн диаграммаларын пайдаланып келесімысал есептерді қарастырып көрелік. |