РГЗ Вращающий момент. санктпетербургский горный университет
 Скачать 300.34 Kb. Скачать 300.34 Kb.
|
|
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ  МИНИСТЕРСТВО науки и высшего ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования «САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ» Кафедра общей и технической физики РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА По дисциплине Физика (наименование учебной дисциплины согласно учебному плану) Тема работы: Механика. Динамика вращательного движения Выполнил: студент гр. . (шифр группы) (подпись) (ФИО) Оценка: Дата: Проверил Руководитель работы: Доцент Тупицкая Н.А. (должность) (подпись) (ФИО) ТЕОРЕТИЧЕСКАЯ ЧАСТЬ Угловая скорость телакинематическая характеристика направления и быстроты вращения тела, она равна отношению вектора элементарного поворота тела к продолжительности этого поворота.  или или 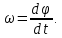 (1) (1)угол поворота тела рад. угловая скорость тела рад/с. tвремя с. Угловое ускорениевектор, характеризующий быстроту изменения угловой скорости тела.  (2) (2)угловое ускорение рад/ 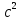 . .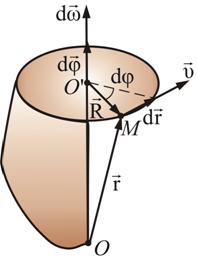 Рис. 1 Момент силы F относительно неподвижной точкиOэто векторное произведение радиус-вектора r, проведенного из точки O в точку N, приложения силы F, на саму эту силу. M=rF. (3) Вектор M направлен перпендикулярно плоскости векторов r и F по правилу правого винта (рис. 2). Модуль момента силы 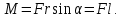 (4) (4) 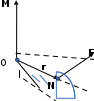 Рис.2 Mмомент силы Н*м. r sin=lдлина перпендикуляра, опущенного из точки O на линию действия силы F, плечо силы м. Момент импульса L материальной точки относительно неподвижной точки Oэто векторное произведение радиуса-вектора r материальной точки, проведенного из точки O, на импульс этой материальной точки p=mv(рис. 3). L=rmv=rp. (5) 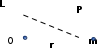 Рис.3 Lмомент импульса материальной точки кг* 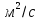 . .mмасса тела кг. Уравнение моментовпроизводная по времени от момента импульса механической системы относительно неподвижной точки равна главному моменту относительно той же точки всех внешних сил, действующих на систему.  (6) (6)Момент инерции тела относительно данной оси Jэто мера инертности тела при вращательном движении. Момент инерции зависит от распределения массы относительно оси вращения, выполняет роль массы при вращательном движении.  (7) (7)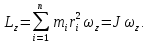 (8) (8) (9) (9)Jмомент инерции относительно оси кг*  . .РАСЧЕТНАЯ ЧАСТЬ Задача Диск массой m=0,5 кг вращается вокруг оси (ось перпендикулярна плоскости диска), проходящей через его центр масс, согласно закону =(t). Найти результирующий момент силы (  ), действующий на диск, и момент импульса тела относительно оси z ( ), действующий на диск, и момент импульса тела относительно оси z ( ) в момент времени t= 5 с. ) в момент времени t= 5 с.Построить графики зависимости момента силы M=M(t) имомента импульса L=L(t) от времени. Данные величины:  ; A= 7,5* ; A= 7,5*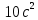 ; B= ; B= ;С= 22 рад; t= 5c; m= 5* ;С= 22 рад; t= 5c; m= 5*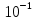 кг; R= кг; R= 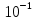 м мРешение  С помощью закона 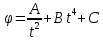 найдем угловую скорость и угловое ускорение диска, которые соответственно являются первыми и вторыми производными от по времени. найдем угловую скорость и угловое ускорение диска, которые соответственно являются первыми и вторыми производными от по времени.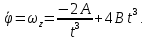 (1.1) (1.1)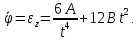 (1.2) (1.2)Запишем выражения для вычисления момента импульса и момента силы. По формулам (8) и (9), где 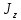 это момент инерции диска относительно оси Z равный это момент инерции диска относительно оси Z равный 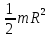 : : (1.3) (1.3) (1.4) (1.4)Подставим данные значения в формулы (1.3) и (1.4)  Проверка размерности:  =кг* =кг* *( *(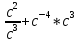 )= кг* )= кг* * * 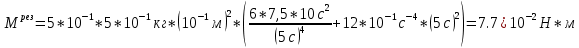 Проверка размерности:  =кг* =кг* *( *( )= кг* )= кг* * *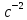 Ответ: 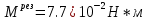 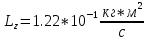 Графики L 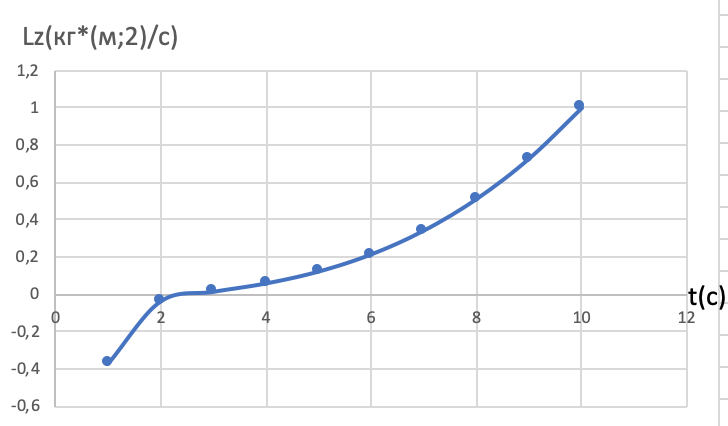  =L(t) =L(t)M  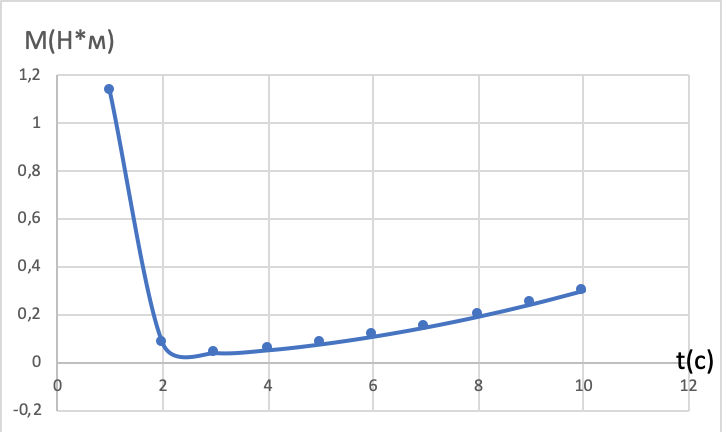 =M(t) =M(t)Вывод: В ходе данной работы были изучены такие явления как угловая скорость тела, угловое ускорение, момент силы, момент импульса, уравнение моментов и момент инерции. На основе изученных закономерностей были посчитаны значения моментов силы ( 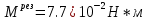 ) и импульса ( ) и импульса (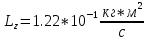 ), требуемые в условии задачи. Благодаря выражениям, выведенным при решении задачи, были построены графики зависимости данных величин от времени L=L(t) и M=M(t). ), требуемые в условии задачи. Благодаря выражениям, выведенным при решении задачи, были построены графики зависимости данных величин от времени L=L(t) и M=M(t). |
