ДЗ Метрология. ДЗ Метрология. Михайлов А.. СанктПетербургский государственный электротехнический университет лэти им. В. И. Ульянова (Ленина) Кафедра иист идз по дисциплине Метрология и измерительная техника
 Скачать 434.24 Kb. Скачать 434.24 Kb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра ИИСТ ИДЗ по дисциплине «Метрология и измерительная техника»
Санкт-Петербург 2021 1. Характеристика средств измерений Характеристики свойств средств измерений, оказывающие влияние на результаты измерений и их точность, называются метрологическими характеристиками средств измерений. Они бывают двух видов: 1. Метрологические характеристики, в которых используется информация о размере единицы измерения. К этому виду относятся следующие группы метрологических характеристик: 1.1. Характеристики, предназначенные для определения результатов измерений (до внесения поправок): функция преобразования измерительного преобразователя, а также измерительного прибора с неименованной шкалой или со шкалой, отградуированной в единицах, отличных от единиц входной величины; значение однозначной или значения многозначной меры; цена деления шкалы измерительного прибора или многозначной меры; цена единицы наименьшего разряда кода средств измерений, предназначенных для выдачи результатов в цифровом коде. 1.2. Характеристики качества показаний — точности и правильности. Точность показания определяется его средним квадратическим отклонением или его аналогом. Правильность обеспечивается внесением поправки, устанавливаемой при испытаниях средства измерений в целях утверждения типа. Эта поправка является одной из составляющих суммарной поправки, которая вносится в показание средства измерений. 1.3. Динамические характеристики средств измерений (полные и частные), учитывающие их инерционные свойства в особых условиях, когда измеряемая величина меняется во времени. 2. Метрологические характеристики, в которых не используется информация о размере единицы измерения. К этому виду относятся следующие группы метрологических характеристик: 2.1. Характеристики, предназначенные для определения результатов измерений (до внесения поправок). К ним относятся: вид выходного кода, число разрядов кода, если средство измерений предназначено для выдачи результатов в цифровом коде. 2.2. Характеристики чувствительности средств измерений к влияющим величинам. К ним относятся функции плияния и учета изменений метрологических характеристик средств измерений, вызванных изменениями влияющих величин в установленных пределах. 2.3. Характеристики взаимодействия с объектами или устройствами на входе и выходе средств измерений. Примерами характеристик этой группы являются входной и выходной импедансы линейного измерительного преобразователя. 2.4. Неинформативные параметры выходного сигнала, обеспечивающие нормальную работу устройств, подключенных к средству измерений. Например, выходным сигналом преобразователя напряжения в среднюю частоту следования импулыов является последовательность импульсов. Для определения значения измеряемого напряжения к выходу преобразователя подключается частотомер. Он будет нормально работать только в случае, если амплитуда и форма импульсов прео6разователя, хотя они и не несут информации о значении измеряемого напряжения, удовлетворяют определенным требованиям. В противном случае частотомер будет измерять частоту следования этих импульсов неточно либо вообще не будет работать.  Изобразим схему измерения:  Здесь R – входное сопротивление вольтметра, r – внутреннее сопротивление источника. Имеем замкнутый контур. По закону Кирхгофа можем записать 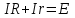 , , где 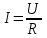 - ток, протекающий в контуре. Тогда для двух измерений получим: - ток, протекающий в контуре. Тогда для двух измерений получим: 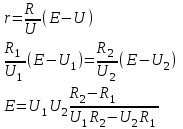 Подставим результаты измерений: 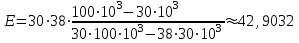 В. В. Оценим максимальное значение абсолютной погрешности. Так как измерения проводятся одним прибором, считаем погрешности коррелированными: 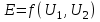 ; ; 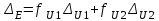 . . Класс точности вольтметра задан как предел приведенной погрешности, отсюда находим максимальные значений абсолютных погрешностей измерений: 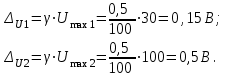 Вычислим значения частных производных  Подставим и определим максимальное значение абсолютной погрешности: 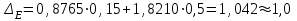 В. В. Максимальное значение относительной погрешности: 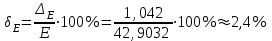 . . Результат измерения эдс: 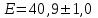 (В). (В). Ответ: ЭДС 40,9 В, абсолютная погрешность 1,0 В, относительная погрешность 2,4%.  А). Схема измерения: амперметр подключен последовательно сопротивлению, вольтметр измеряет падение напряжения на амперметре и сопротивлении. 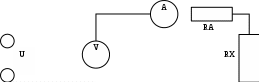 1) методическая погрешность Согласно закона Ома, сопротивление равно 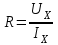 . . 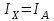 - показания амперметра, - показания амперметра, 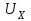 - напряжение на сопротивлении. - напряжение на сопротивлении. В данной схеме вольтметр измеряет падение напряжение на сопротивлении и амперметре, поэтому 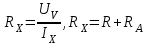 . . Абсолютная погрешность равна 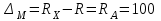 Ом = 0,1 кОм. Ом = 0,1 кОм. Относительная погрешность равна 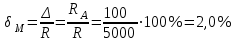 . . Методическая погрешность завышает результат измерения на величину сопротивления амперметра. 2) инструментальная погрешность Считаем погрешности некоррелированными. Тогда относительная погрешность измерения равна: 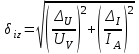 Показания приборов: 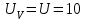 В. В. 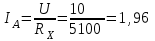 мА. мА. Погрешности заданы в виде приведенных погрешностей. 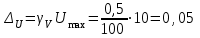 В. В. 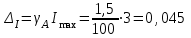 мА. мА.Подставим 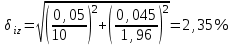 . . Абсолютная погрешность: 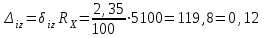 кОм. кОм. б) Схема измерения: вольтметр подключен параллельно сопротивлению, амперметр последовательно измеряет ток на вольтметре и сопротивлении. 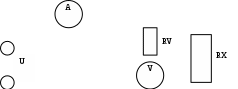 Согласно закона Ома, сопротивление равно 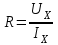 . . 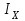 - ток, протекающий через сопротивление, - ток, протекающий через сопротивление, 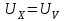 - напряжение на сопротивлении. - напряжение на сопротивлении. В данной схеме амперметр измеряет ток, протекающий через сопротивление и вольтметр, поэтому 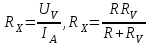 . . Абсолютная погрешность равна 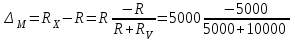 = -1667 Ом = -1,7 кОм. = -1667 Ом = -1,7 кОм. Относительная погрешность равна 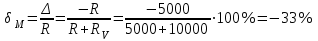 . . Методическая погрешность занижает результат измерения. 2) инструментальная погрешность Считаем погрешности некоррелированными. Тогда относительная погрешность измерения равна: 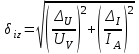 Показания приборов: 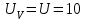 В. В. 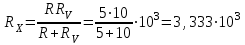 Ом = 3,3 кОм. Ом = 3,3 кОм. 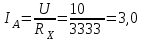 мА. мА. Погрешности заданы в виде приведенных погрешностей. 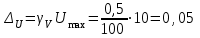 В. В. 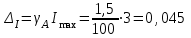 мА. мА.Подставим 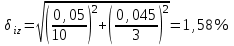 . . Абсолютная погрешность: 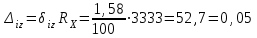 кОм. кОм. Доверительный интервал 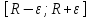 , где R = 105,8 Ом – среднее значение результата измерения; , где R = 105,8 Ом – среднее значение результата измерения; 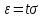 - величина ошибки для заданной доверительной вероятности Р и числа измерений n = 10; t – квантиль распределения Стьюдента; σ – оценка среднего квадратического отклонения среднего значения. - величина ошибки для заданной доверительной вероятности Р и числа измерений n = 10; t – квантиль распределения Стьюдента; σ – оценка среднего квадратического отклонения среднего значения. Оценка среднего квадратического отклонения среднего значения равна 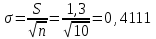 Ом. Ом. А) доверительная вероятность Р = 0,9. По таблице значений распределения Стьюдента для Р = 0,9 и n = 10 определяем t = 1,833. 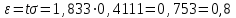 Ом. Ом. Доверительный интервал 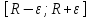 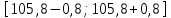 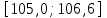 Б) доверительная вероятность Р = 0,95. По таблице значений распределения Стьюдента для Р = 0,95 и n = 10 определяем t = 2,262. 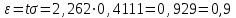 Ом. Ом. Доверительный интервал 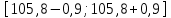 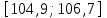 В) доверительная вероятность Р = 0,98. По таблице значений распределения Стьюдента для Р = 0,98 и n = 10 определяем t = 2,821. 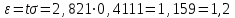 Ом. Ом. Доверительный интервал 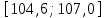  Класс точности задан в виде c/d. Выражение для относительной погрешности измерения: 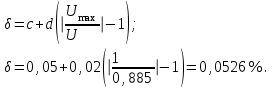 Абсолютная погрешность 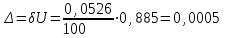 В. В. Результат измерения 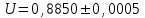 (В). (В). |
