матиматика. 192340_б1-ТПЭНз-21_Фролов_Юрий_Владимирович_2021_7. Саратовский государственный
 Скачать 250.5 Kb.
|
|
САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. ГАГАРИНА Ю.А. Ф   акультет ИнЭТС Курс 2С  пециальность б1-ТПЭНз-21Ш   ифр 192340 Вариант 10Контрольная/курсовая р  абота № 3п  о Высшей математике(наименование дисциплины) Н  а тему (полное название темы или номер варианта) С  тудента Фролов Юрий Владимирович(фамилия, имя и отчество полностью)  Дата отправки работы Отметка о зачете работы: в  университет Д  ата регистрации работы в  университете  Контрольная работа №3 Вариант №10 Задание № 1. Найти аналитическую функцию  по заданной действительной  (или мнимой  ) части и значению  : ,  .Решение. Задачу можно решить лишь в том случае, если функция является гармонической, т.е. удовлетворяет уравнению Лапласа. Имеем, ,    .Таким образом, функция является гармонической.Из первого условия Коши – Римана  имеем  .Используя второе условие Коши – Римана  , получаем   .Тогда  , а функция  .Найдем  из условия . Имеем, .Таким образом,  .Задание № 2. Вычислить интеграл от функции комплексной переменной, используя основную теорему о вычетах:  ,  :  .Решение. Изолированными особыми точками подынтегральной функции будут точки в которых знаменатель дроби обращается в ноль, т.е.     Таким образом, изолированными особыми точками подынтегральной функции являются  ,  ,  , и из них  и  находятся внутри области, ограниченной окружностью . Найдем вычеты в этих точках. Имеем  . Следовательно,  , .По основной теореме о вычетах имеем  .Таким образом,  .Задание № 3. Операционным методом решить задачу Коши:  ,  .Решение. Пусть искомая функция  – оригинал, а  – ее изображение. Тогда , ,а так как  , то дифференциальное уравнение примет вид:    .Используя таблицу преобразования Лапласа, получаем:  ,  ,  ,   .Таким образом, решение задачи Коши будет функция .Задание № 4. В первой урне 4 белых и 8 черных шаров, а во второй урне 5 белых и 8 черных шаров. Из первой урны случайным образом вынимают 3 шара и опускают во вторую урну. После этого из второй урны также случайно вынимают 3 шара. Найти вероятность того, что все шары, вынутые из второй урны, белые. Решение. Рассмотрим события:  {из первой урны во вторую переложили три белых шара}, {из первой урны во вторую переложили два белых и один черный шар}, {из первой урны во вторую переложили один белый и два черных шара}, {из первой урны во вторую переложили три черных шара}, {из второй урны достали только белые шары}.Вероятности гипотез равны: 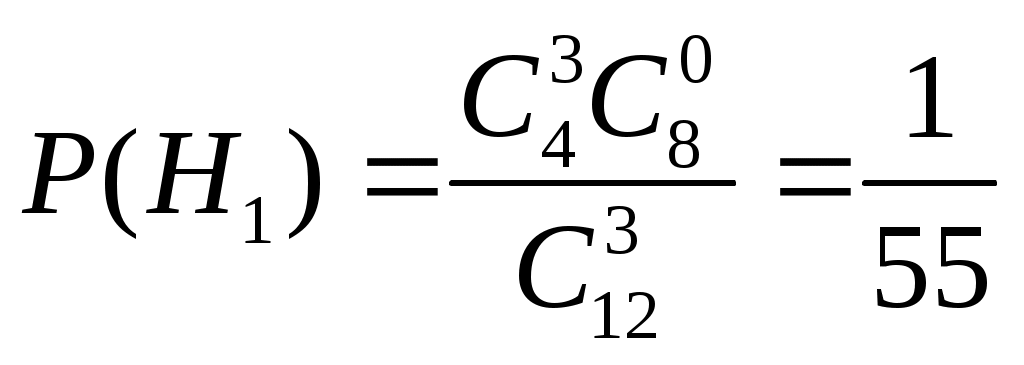 ,  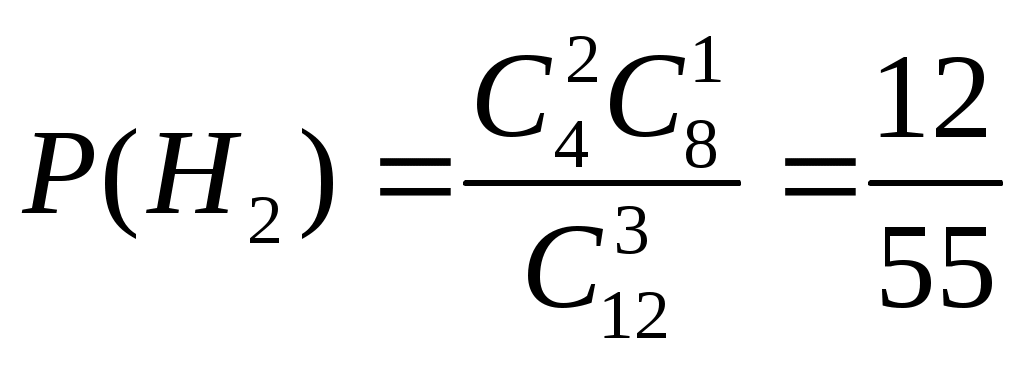,  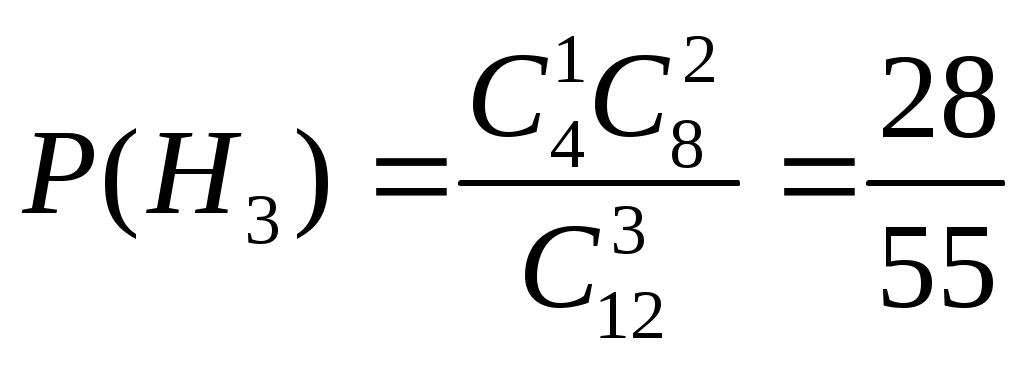,  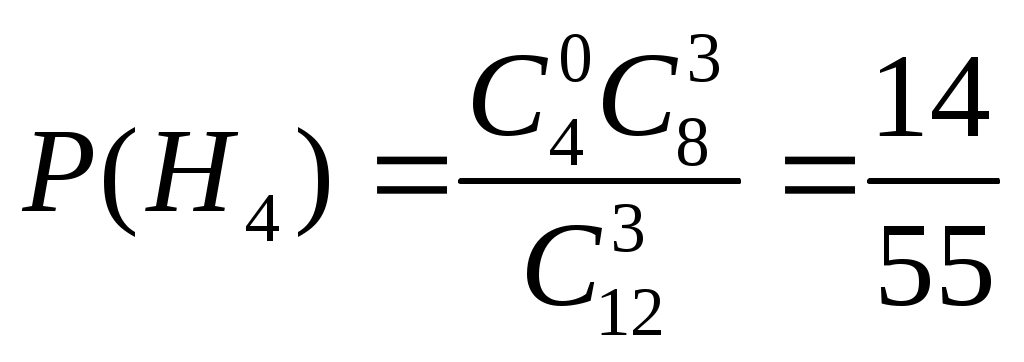.Найдем вероятности достать из второй урны только белые шары в предположении реализации одной из гипотез:  ,  ,  ,  .Подставляя найденные вероятности в формулу полной вероятности, получаем:   .Таким образом, вероятность того, что из второй урны достали только белые шары равна 0,038. Задание № 5. Непрерывная случайная величина 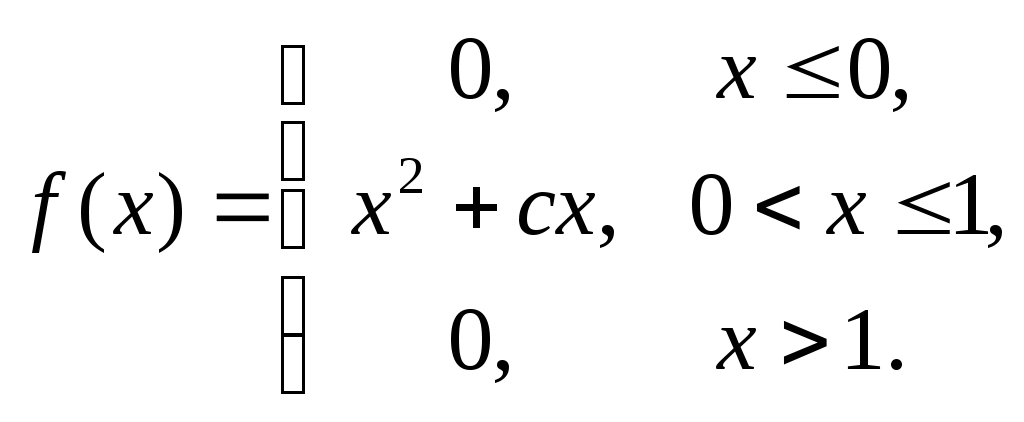 задана плотностью распределения Требуется найти: а) параметр  ; б) функцию распределения  ; в) математическое ожидание  и дисперсию  .Решение. а) Воспользуемся условием нормировки плотности распределения      .б) Для нахождения функции распределения воспользуемся формулой:  .Тогда, при  :  ;при  :  ;при  :  .Таким образом, 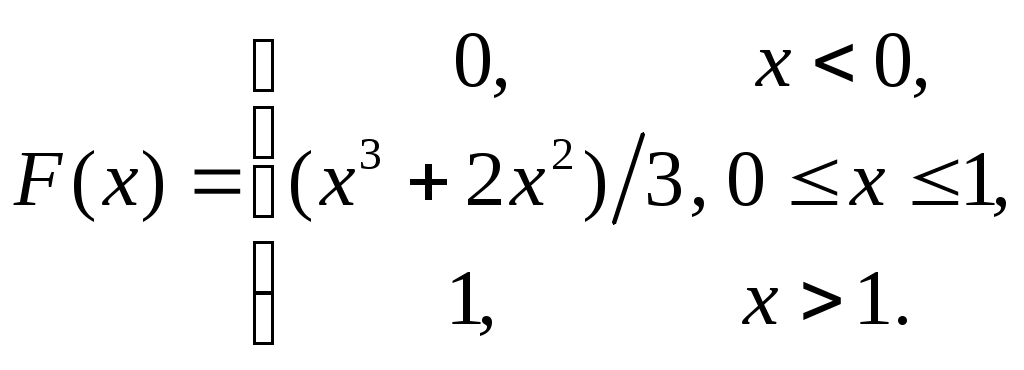 в) Найдем математическое ожидание и дисперсию величины : , .Список литературы1. Дифференциальное и интегральное исчисление. Т.2 Н.С. Пискунов, М. Интеграл-пресс.2007. 2. Сборник задач по математике для втузов. Ч.3. Под ред. А.В. Ефимова и А.С. Поспелова, М., ФМ, 2004. 3. Высшая математика в упражнениях и задачах. Ч.2. П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова, М.: Высш. школа, 2009. 4. Сборник заданий по специальным курсам высшей математики. Типовые расчеты: Учебное пособие. В.Ф. Чудесенко, Лань, 2005. 5. Высшая математика в примерах и задачах: Т.2. В.Д. Черненко, СПб.: Политехника, 2003. 6. Руководство к решению задач по теории вероятностей и математической статистике. Учеб. пособие. В.Е. Гмурман. М.: Высшее образование. 2006. Работу выполнил: |