ЗАДАНИя ДИСКР МАТЕМ ЧАСТЬ 2. Сборник контрольных заданий по дискретной математике
 Скачать 1.76 Mb.
|
|
Задача 3. По матрице инцидентности построить остовное дерево графа. Составить список ветвей и хорд графа. Построить граф. 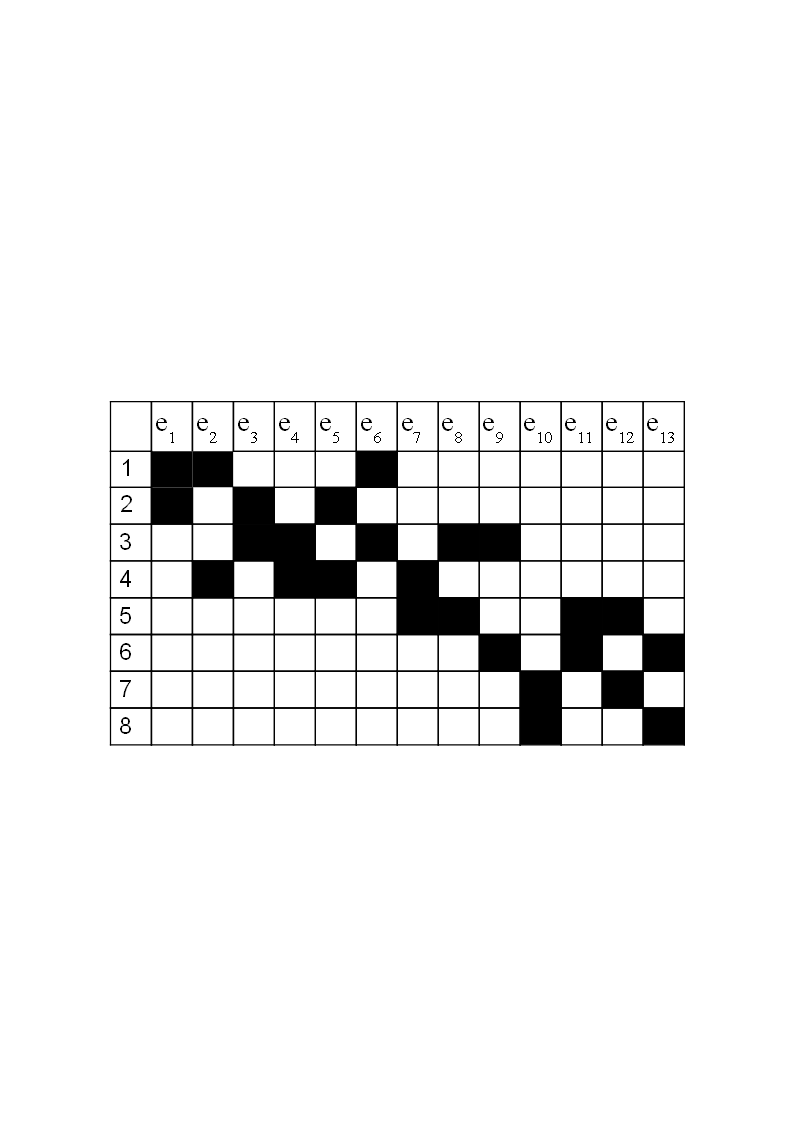 В начале выбираем некоторую вершину графа, например  . Тогда получаем разбиение множества вершин графа:  . Кроме этого формируем множество  ветвей остова. На первом шаге  . Далее выбираем очередное ребро остова так, что одна его вершина  , а другая  Присоединяем к множеству  вершину  , а к множеству ребро  . Проверка на окончание: если  , где  - множество вершин исходного графа, то алгоритм заканчивает свою работу. Дерево  есть искомое остовное дерево. Рассмотрим работу алгоритма на примере. Пусть матрица инцидентности имеет вид, показанный на рисунке. 1 итерация: Шаг 1:  ,  Шаг 2:  , поэтому переходим на начало 1 шага2 итерация: Шаг 1:  ,  Шаг 2: , поэтому переходим на начало 1 шага3 итерация: Шаг 1:  ,   Шаг 2: , поэтому переходим на начало 1 шагаДалее ребра  не могут быть выбраны, так как их вершины принадлежат множеству . Поэтому на следующей итерации выбираем ребро  .4 итерация: Шаг 1:  ,  Шаг 2: , поэтому переходим на начало 1 шага5 итерация: Шаг1:  ,   Шаг 2: , поэтому переходим на начало 1 шага6 итерация: Шаг 1:  ,  Шаг 2: , поэтому переходим на начало 1 шага7 итерация: Шаг 1:  ,  Шаг 2: , конец работы алгоритма.В результате получаем множество ветвей остова:   Соответственно множество хорд:  .Строим граф (см. матрицу инцидентности). Жирным выделен остов. 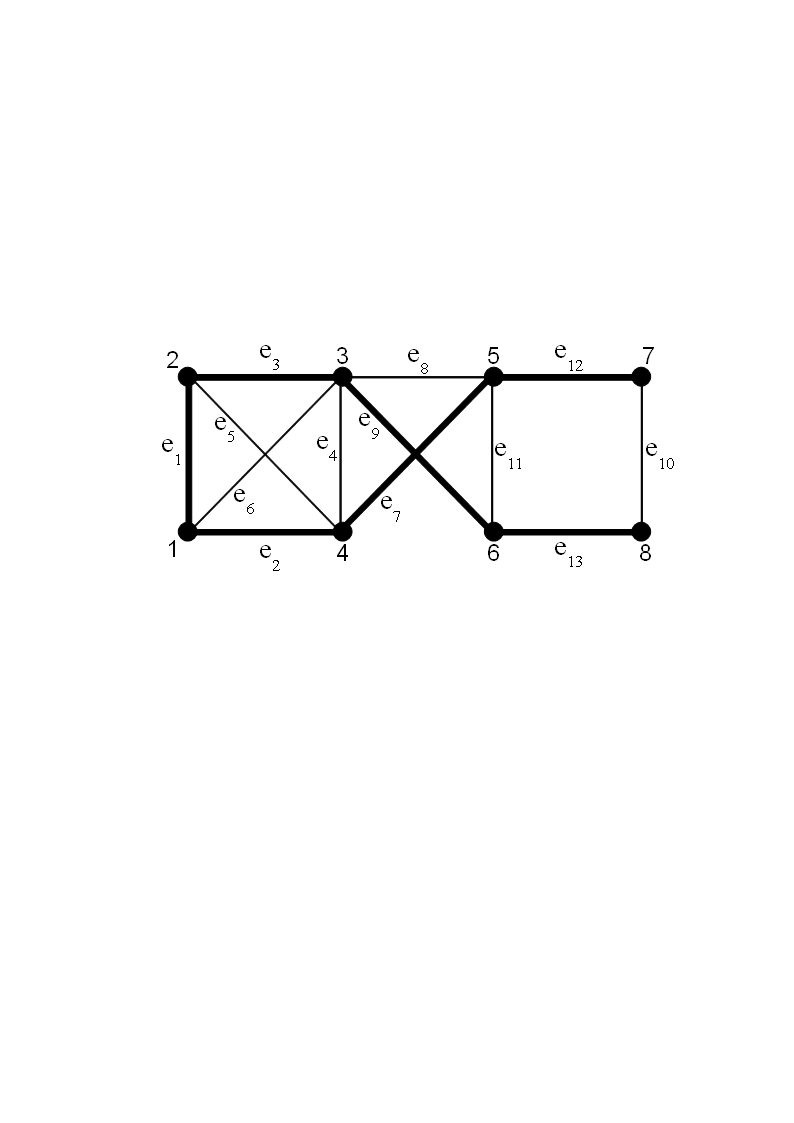 Задача 4. Решим задачу 4 для автомата, заданного своей диаграммой состояний: 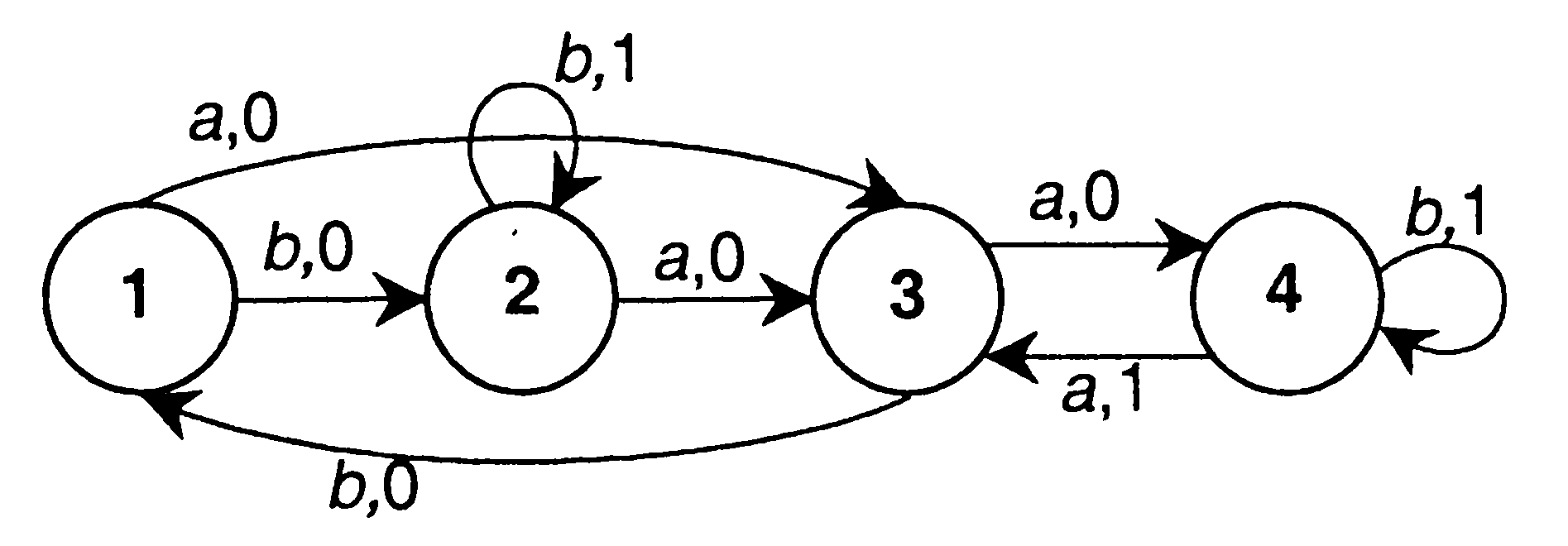 Изобразим таблицу данного автомата (Таблица 1а). Таблица 1а.  По данному неинициальному автомату Мили  строим эквивалентный ему автомат Мура  следующим образом:Автомат содержит  состояний, каждое из которых мы будем помечать двумя символами. Состояния автомата обозначим так:  ,  ,  ,  ,  ,  ,  ,  ,  ,  ,  ,  .Функция отметок  на состояниях , , , не определена, а её значения на состояниях , , …, задаются с помощью функции выходов  автомата :  , где  ,  .То есть  , … ,  .Функция переходов  на состояниях, содержащих в изображении символ  , определяется так:  , , .В остальных случаях первый символ имени нового состояния совпадает со считываемым символом входного автомата, а второй символ нового состояния определяется с помощью функции переходов  автомата :  , где  ,  .Получим:  ,  , т.к.  , и т.д.Запишем таблицу состояний полученного автомата Мура. 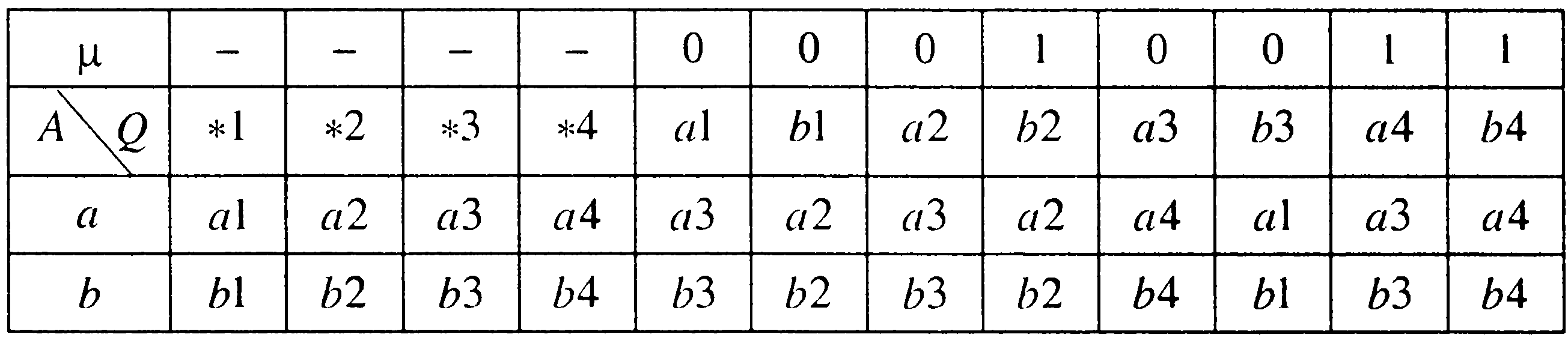 Проверим работу исходного автомата над словом 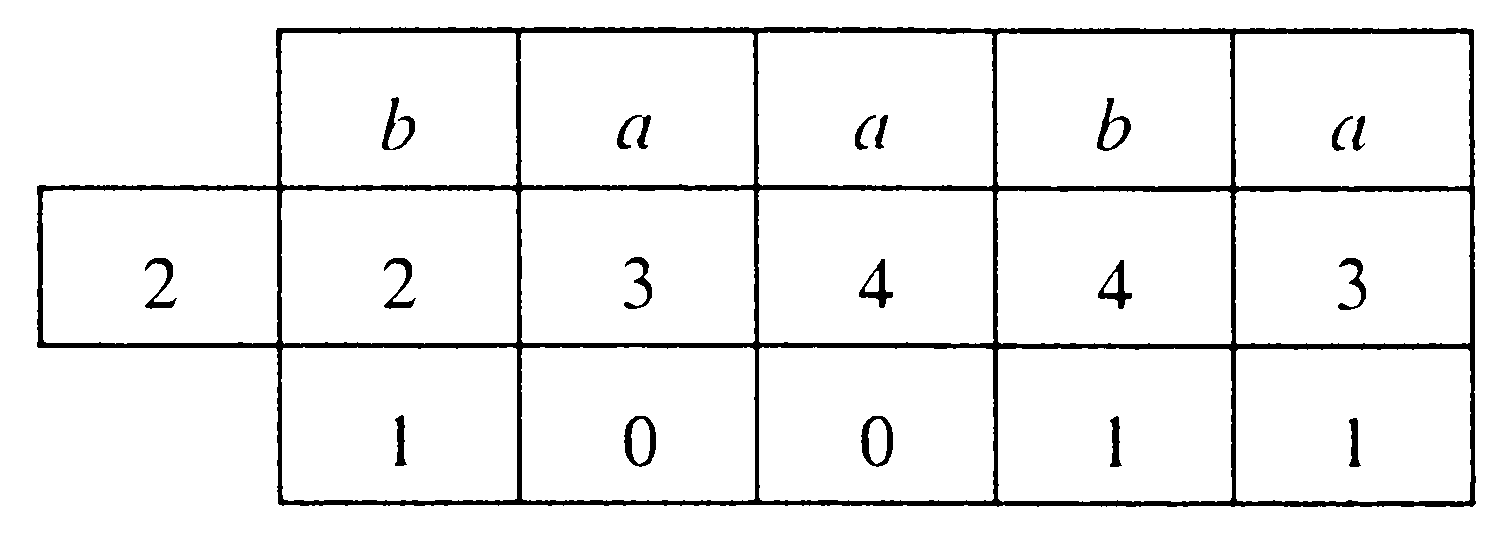 , запустив его из 2 состояния: Построенный автомат Мура запускаем из состояния 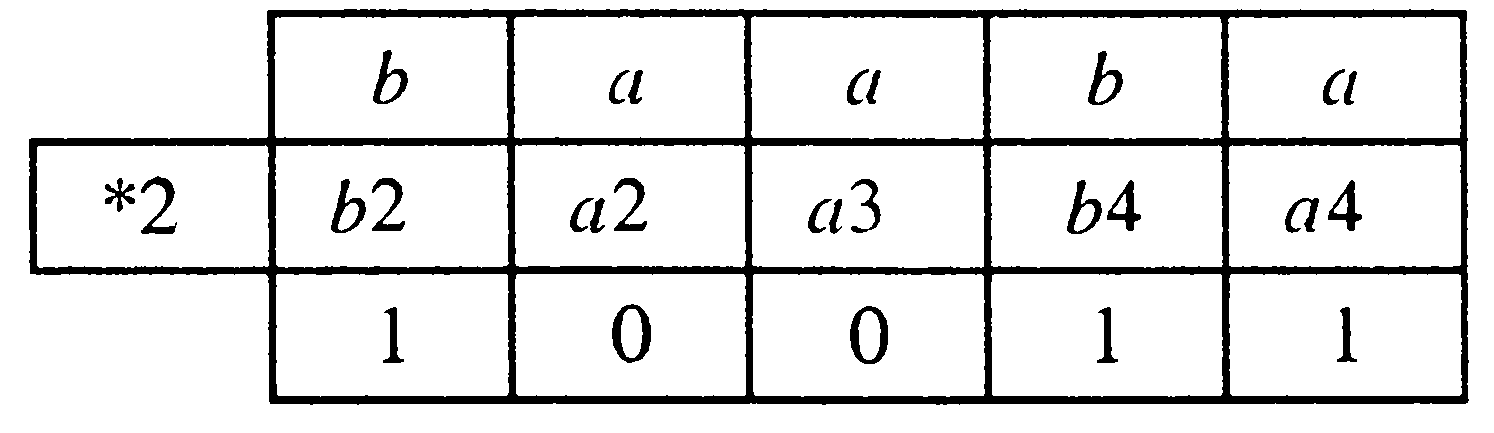  Как видим, результаты обоих автоматов совпали. |