ЗАДАНИя ДИСКР МАТЕМ ЧАСТЬ 2. Сборник контрольных заданий по дискретной математике
 Скачать 1.76 Mb.
|
|
4. а) Написать таблицу состояний данного автомата. б) Считая автомат неинициальным, построить эквивалентный автомат Мура. Проверить работу данного и построенного автоматов над одним и тем же словом. 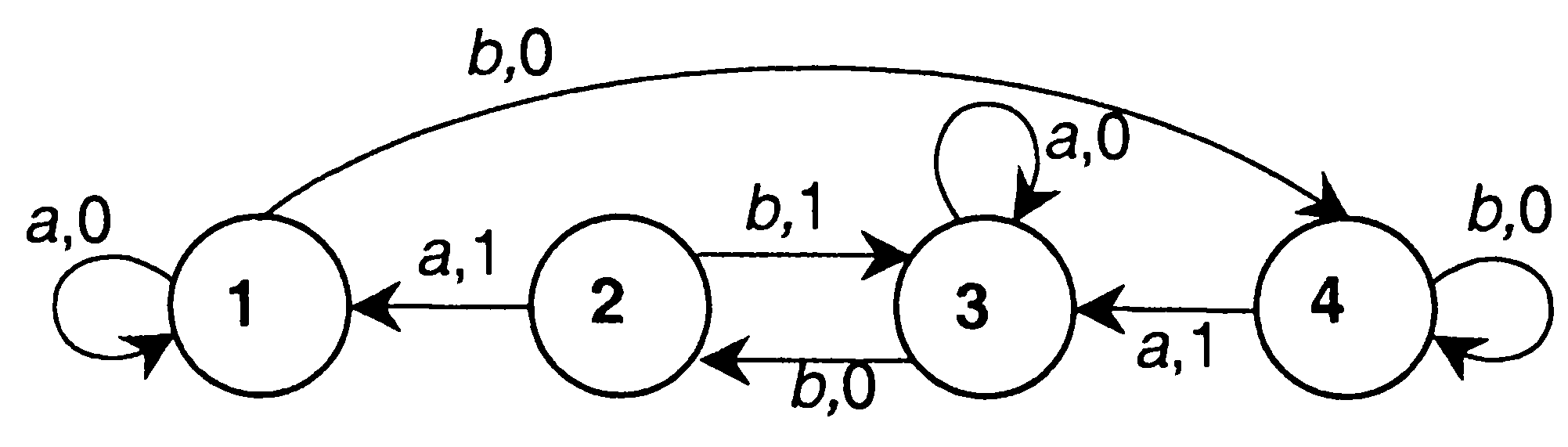 Вариант 28 1  . С помощью алгоритма Дейкстры найти путь минимального веса между вершинами s и t в нагруженном графе.2  . Найти максимальный поток в заданной транспортной сети, используя алгоритм Форда-Фалкерсона. Проверить ответ по теореме Форда-Фалкерсона (найти минимальный разрез графа сети).3. По матрице инцидентности построить остовное дерево графа. Составить список ветвей и хорд графа. Построить граф.
4. а) Написать таблицу состояний данного автомата. б) Считая автомат неинициальным, построить эквивалентный автомат Мура. Проверить работу данного и построенного автоматов над одним и тем же словом. 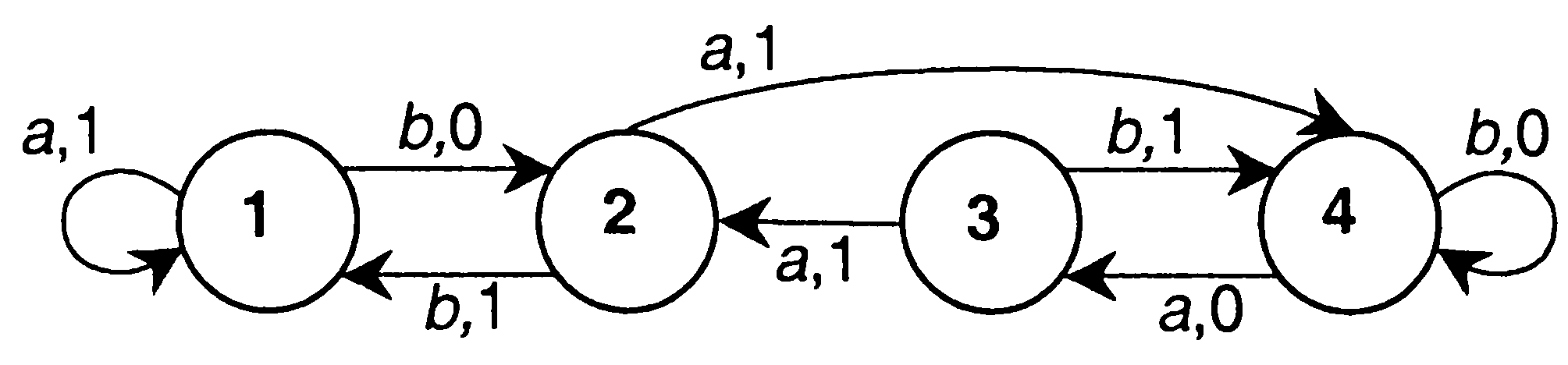 Вариант 29 С помощью алгоритма Дейкстры найти путь минимального веса между вершинами s и t в нагруженном графе.  Найти максимальный поток в заданной транспортной сети, используя алгоритм Форда-Фалкерсона. Проверить ответ по теореме Форда-Фалкерсона (найти минимальный разрез графа сети).  3. По матрице инцидентности построить остовное дерево графа. Составить список ветвей и хорд графа. Построить граф. 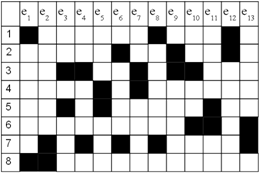 4. а) Написать таблицу состояний данного автомата. б) Считая автомат неинициальным, построить эквивалентный автомат Мура. Проверить работу данного и построенного автоматов над одним и тем же словом.  Вариант 30 С помощью алгоритма Дейкстры найти путь минимального веса между вершинами s и t в нагруженном графе. 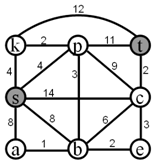 Найти максимальный поток в заданной транспортной сети, используя алгоритм Форда-Фалкерсона. Проверить ответ по теореме Форда-Фалкерсона (найти минимальный разрез графа сети).  3. По матрице инцидентности построить остовное дерево графа. Составить список ветвей и хорд графа. Построить граф.  4. а) Написать таблицу состояний данного автомата. б) Считая автомат неинициальным, построить эквивалентный автомат Мура. Проверить работу данного и построенного автоматов над одним и тем же словом. 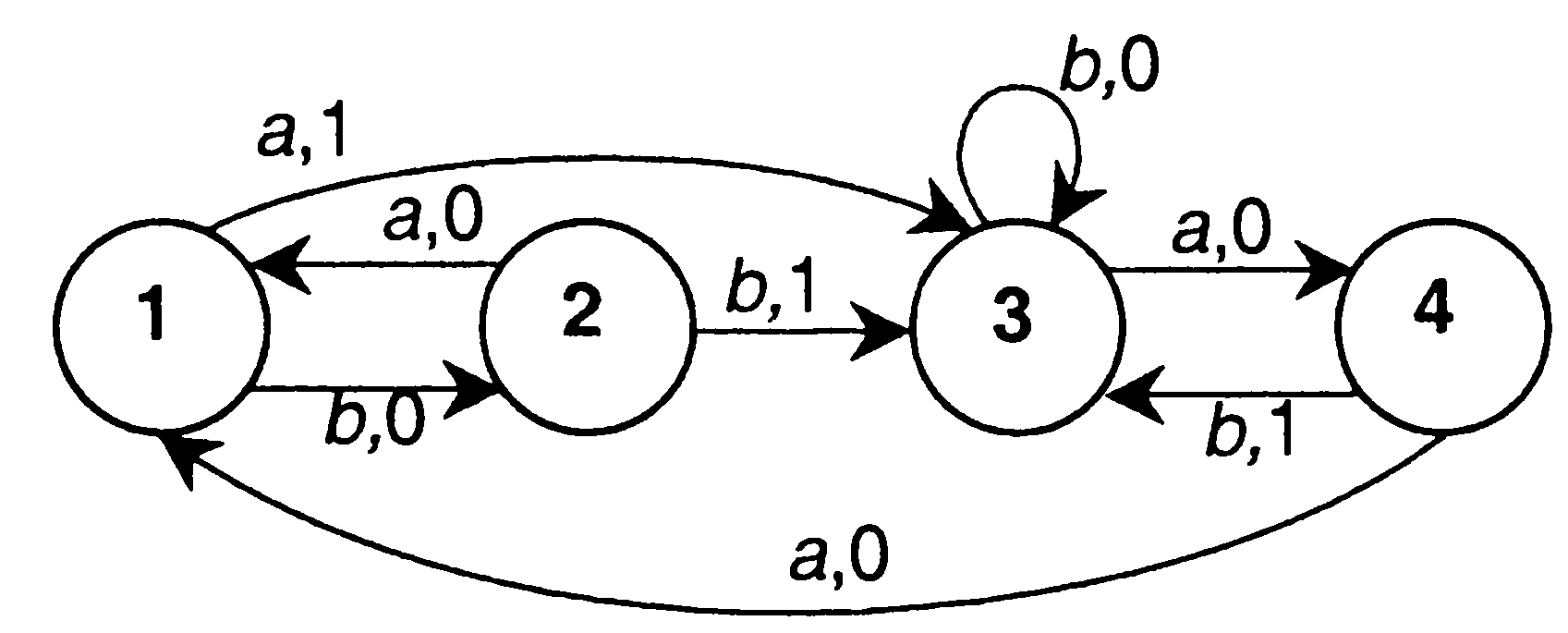 Решение типового варианта Задача 1. С помощью алгоритма Дейкстры найти путь минимального веса между вершинами s и t в нагруженном графе.  Решение. Полагаем:  1 итерация: текущая вершина с постоянной меткой 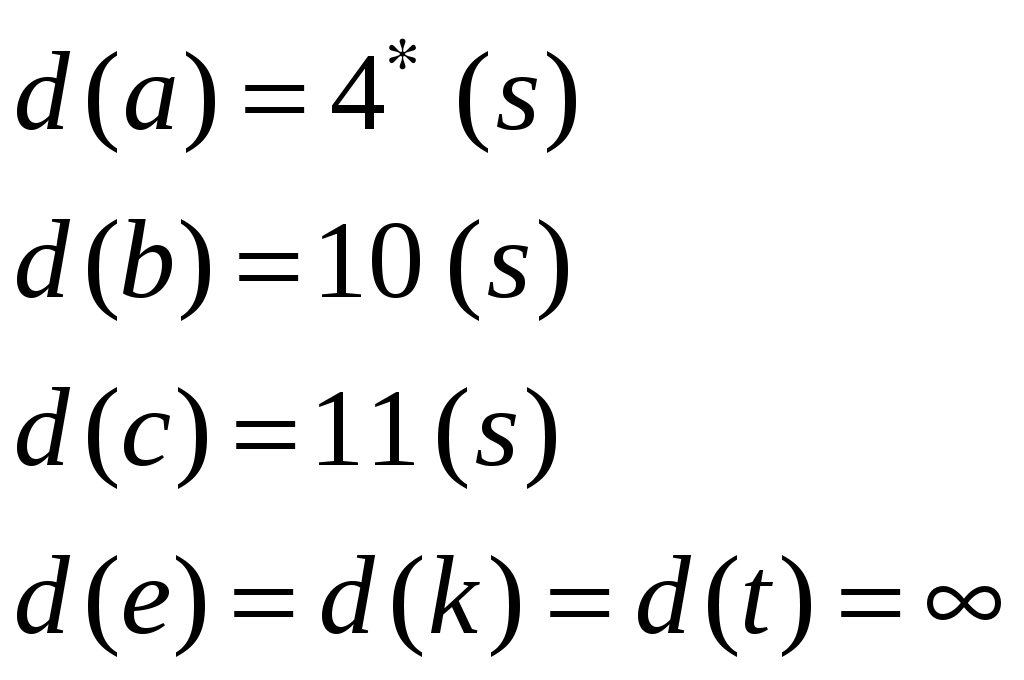 , далее расставляем метки у вершин, достижимых из s  В скобках указана та вершина, через которую модифицируется метка рассматриваемой вершины (на первой итерации везде стоит вершина s). Звездочкой отмечена наименьшая метка из чисел 4, 10, 11. При этом данная метка будет постоянной (в нашем случае 4). 2 итерация: текущая вершина с постоянной меткой  , далее меняем метки у вершин с временными метками (меняются лишь метки тех вершин, которые достижимы из вершины y) Метка а, стоящая в скобке в строчке для  , означает, что путь из s в b, проходящий через вершину а, короче пути, состоящего из одной дуги  . Аналогично в двух других случаях (2 и 4 строка). 3 итерация: текущая вершина с постоянной меткой 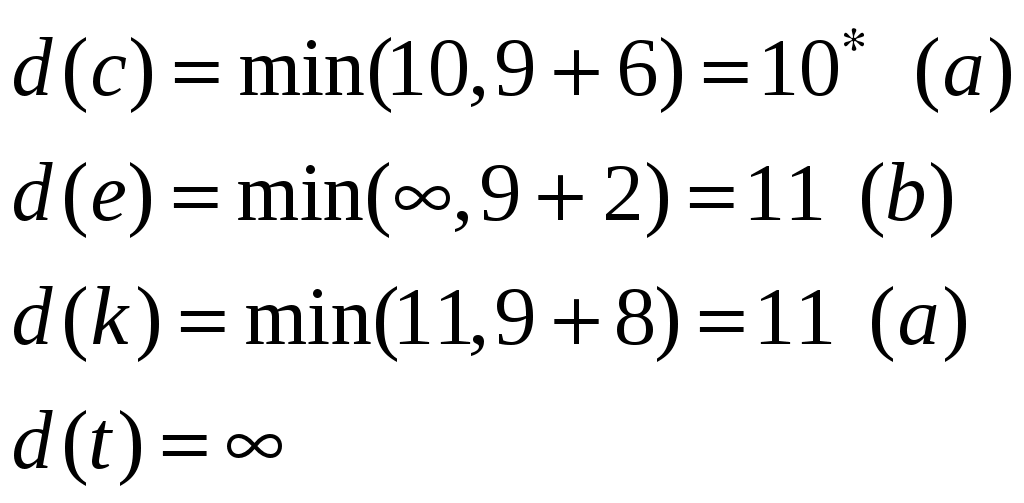 ,  4 итерация: текущая вершина с постоянной меткой 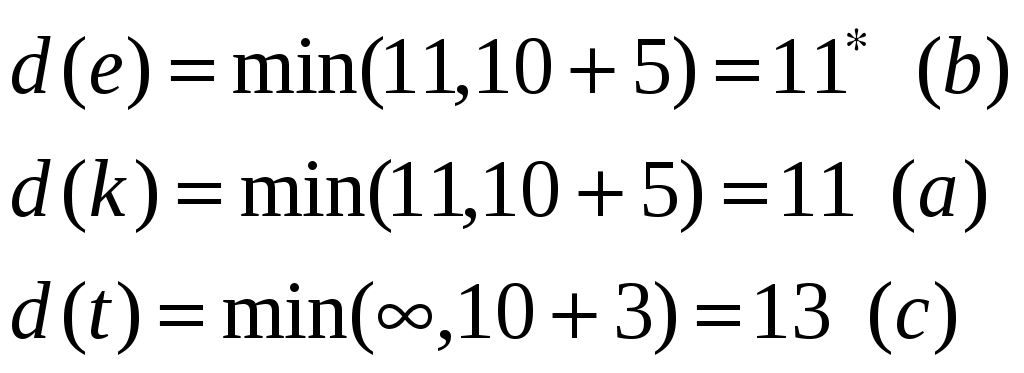 ,  Имеем 2 одинаковые метки с минимальным значением, поэтому выбираем любую из них (в данном случае  )5 итерация: текущая вершина с постоянной меткой 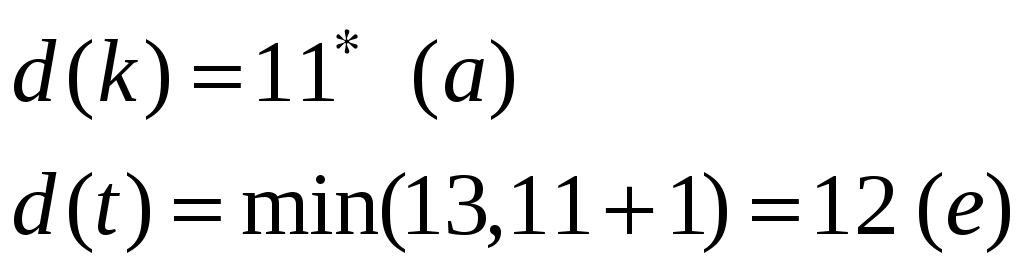 ,  6 итерация: текущая вершина с постоянной меткой  ,  Вершина t имеет постоянную метку, следовательно 12 – длина кратчайшего пути от s до t. Сам путь находим по меткам, расставленным в скобках. А именно, вершине t предшествует e, что видно из 2 строки 5 итерации. Из 1 строки 4 итерации видим, что e предшествует b. Из 1 строки 2 итерации видим, что b предшествует a. Из 1 строки 1 итерации следует, что a предшествует s. Таким образом, имеем путь s-a-b-e-t. Видим, что его длина 12 (см. рисунок графа). Задача 2. Найти максимальный поток в заданной транспортной сети, используя алгоритм Форда-Фалкерсона. Проверить ответ по теореме Форда-Фалкерсона (найти минимальный разрез графа сети). Алгоритм решения задачи о максимальном потоке. 1°. Положить ff0, c пропускным способностям заданной транспортной сети. 2°. Переприсвоить: fff. Вычислить остаточные пропускные способности c, отвечающие пропускным способностям c и потоку f. 3°. Для транспортной сети спропускными способностями c найти путь lиз sвt, обладающий максимальной пропускной способностью. Пусть — пропускная способность этого пути. Если 0 (путь отсутствует), то перейти к пункту 4°; в противном случае переопределить добавочный поток f, полагая 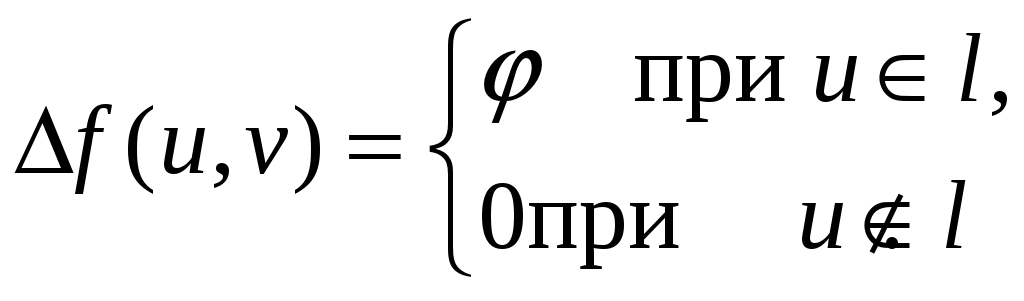 После этого перейти к пункту 2°. 4°. Закончить работу алгоритма. Поток f— ответ задачи. Пусть функция c описывает пропускные способности исходной сети и f — стандартный представитель исходного потока. Тогда остаточные пропускные способности c определяются следующим образом: c(u, v)c(u, v)f(u, v) f(v, u). Пример решения задачи Задан граф транспортной сети 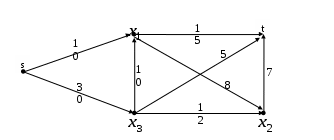   Составляем матрицу пропускных способностей:
Находим путь из s в t как можно большей пропускной способности. Путь максимальной пропускной способности можно найти с помощью алгоритма волны, а для небольшой сети – визуально по графу. Примечание1 Если найден путь не максимальной пропускной способности, алгоритм всё равно даст результат, но число шагов может увеличиться. Примечание2 При решении задачи можно использовать как язык матриц, так и язык графов. Ниже приводятся оба способа записи решения. Путь 1.  . Пропускная способность: 10. Составляем матрицу остаточных пропускных способностей/добавочного потока
При отображении данной информации на графе будем использовать формат A/B/C, где A = c(u,v) – остаточная пропускная способность дуги, B = c(v,u) – остаточная пропускная способность противоположной дуги, C= f(u,v) – добавочный поток через данную дугу. Для дуг, через которые добавочный поток не идёт, третья компонента отсутствует. Остаточные пропускные способности дуг, входящих из s и дуг, исходящих из t вычислять не нужно, на графе они присутствуют для большей наглядности. 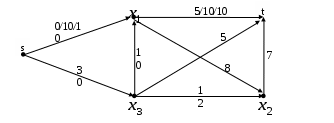 Путь 2.  . Пропускная способность: 7. Матрица остаточных пропускных способностей/добавочного потока:
Соответствующий граф:  Путь 3.  . Пропускная способность: 5. Матрица остаточных пропускных способностей/добавочного потока:
Соответствующий граф:  Путь 4.  . Пропускная способность: 5. Матрица остаточных пропускных способностей/добавочного потока:
Соответствующий граф:  Путь 5. Отсутствует. Алгоритм завершён. Максимальный поток:  Находим проверочный разрез (минимальное сечение). Все дуги, входящие в проверочный разрез, должны быть насыщенными (иметь остаточную пропускную способность 0). В нашем случае это дуги  Искомый разрез (он может быть не единственным) составляют дуги  Графическое изображение проверочного разреза: 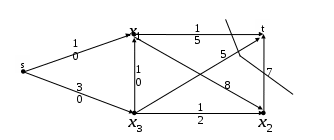 Пропускная способность данного разреза равна 15+5+7=27=П, что соответствует теореме Форда-Фалкерсона. |
