математика в географии. Сборник задач для обучающихся 5 9 классов Невьянск, 2019 Аннотация
 Скачать 1.27 Mb. Скачать 1.27 Mb.
|
1 2      Управление образования Невьянского городского округа муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа №3 Невьянского городского округа «МАТЕМАТИКА В ГЕОГРАФИИ» Сборник задач для обучающихся 5 – 9 классов Невьянск, 2019 Аннотация В данном сборнике собраны наиболее популярные в географии задачи, иллюстрирующие процессы, происходящие в географической оболочке. Данные задачи решаются путем применения математических расчетов и приемов, таких как: составление пропорции, умение составлять и применять математические формулы, знание величин измерения и перевод одних единиц измерения в другие, и др. Данные задачи иллюстрируют основные географические процессы и явления, происходящие в географической оболочке, показывают тесную взаимосвязь двух наук: географии и математики. Помогают вспомнить и закрепить математические навыки и умения обучающихся, подготовиться к сдаче итоговой аттестации по предметам география и математика. Сведения об авторах: Гудкова Наталия Анатольевна, учитель математики МБОУ СОШ №3 НГО Свердловской области. Контактный телефон: 89001985312 Электронный адрес: NataS-2012@yandex.ru Шифельбейн Светлана Викторовна, учитель географии МБОУ СОШ №3 НГО Свердловской области. Педагог дополнительного образования, экологическое объединение «Глобус». Инструктор Детского молодежного экологического движения «Зеленый дозор» г. Североуральска и руководитель Невьянского отделения Детского молодежного экологического движения «Зеленый дозор». Контактный телефон: 89089025379 Электронный адрес:svetlana.shifelbeun@mail.ru СОДЕРЖАНИЕ
Введение Математика и география - это части глобальной науки естествознания. Рассматривая историю формирования математики и географии, мы пришли к выводу о том, что эти науки зародились еще до нашей эры как отдельные области человеческого знания. Изначально они развивались параллельно, независимо друг от друга. Но накопленные знания в этих науках требовали единого языка, который бы позволял не только формулировать, но и транслировать приобретенные в процессе развития наук познания. Язык должен был быть четким и лаконичным, точно описывающим процессы, происходящие в природе. Таким языком оказалась математика. Сегодня мы говорим, что математика является универсальным языком не только географии, но и всех естественных наук. В географии математика встречается повсеместно: в определении масштаба и масштабировании, измерении географических объектов (высота гор, гидрологические исследования), определении и расчете демографических показателей, при обозначении географических координат, в ориентировании (азимут) и др. . Рост численности населения земного шара, строительство новых населенных пунктов, создание антропогенных ландшафтов, открытие и осваивание новых земель, - все это требовало применения математики в географии. Увеличившиеся географические знания необходимо было систематизировать, именно тогда и сливаются две величайшие науки: география и математика. Рассматривая этапы развития математики и географии мы пришли к выводу, что первый опыт слияния этих наук произошел во времена Древней Греции. Родоначальниками данного эксперимента стали древнегреческие ученые Фалес Милетский, Эратосфен, Аристотель, Пифагор, Геродот. В древности математическая география описывала и вычисляла параметры Земли как планеты, проводился расчет ее форм и размеров. Зародился картографический метод описания Земли, создавались первые карты, в частности, на карте Эратосфена, мы уже видим элементы градусной сети - меридианы и параллели. Картографический метод описания Земли требует определенного лаконичного языка и точности, вот здесь на помощь людям приходит математика. Для изображения географических объектов на карте применяется масштаб. Масштаб был придуман ещё до нашей эры Евклидом. В темные (средние) века математика, как и география, испытывает определенный застой в своем развитии. Догмы церкви отвергают большинство естественных наук как средство познания окружающего мира. Но! Приближаясь к эпохе Великих географических открытий, эти науки опять тесно переплетаются между собой в навигации, картографии и топографии. В XIX веке математические методы в географии получают широкое развитие в таких отраслях географии, как климатология и гидрология. Постоянно разрастающаяся сеть гидрометрических и гидрометеорологических станций собирала и собирает сейчас огромное количество данных, которые характеризуют явления, переменные и в пространстве и во времени. Их обработка требует расчёта средних, модальных, средне-экстремальных величин, частот, амплитуд и т. д., т. е. обусловила внедрение в физическую географию методов математической статистики, ставших одним из важнейших инструментов познания физико – географических процессов. Наиболее полное слияние наук происходит в XX веке, когда появляется научная основа применения математики в географии. Именно в это время появляется насущная необходимость применения количественных методов анализа, технических средств обработки данных. Математические методы в географии начинают использоваться как одно из важных средств логической систематизации эмпирического материала (количественных и качественных данных), как способ выявления и отображения количественных зависимостей в исследуемых объектах, а также как особенные формы идеализации и аналогии. В результате чего появляется возможность анализировать объекты, формирующиеся под действием разнообразных факторов, в том числе случайных, все из которых невозможно выделить, выучить и учесть. Использование более точных, по сравнению с описательными методами в географии, математических средств познания, позволяет получить более четкий анализ эмпирического материала, эмпирической проверки гипотез, теорий, законов. Все это дает возможность исследовать самые разнообразные вопросы, находить более точные решения, а также оценивать меру достоверности суждений об исследуемых географических объектах и явлениях. Тем самым осуществляется переход от интуитивных представлений опоследних к логически обоснованным конструкциям, которые поддаются строгой и объективной проверке их соответствия реалиям. Применение средств математической статистики позволяет решать следующие задачи: 1) идентификации, группировки, классификации объектов на основе оценки средних значений; 2) выделения методом главных компонентов наиболее информативных признаков группы; 3) оценка корреляционных связей между признаками для обеспечения возможности прогнозирования неизвестных значений свойств географических объектов по совокупности значений известных признаков. Применение математических методов в географии, в том числе и в физической, изначально определяется запросами практики. Растет количество отраслей хозяйства, нуждающихся в географических материалах. Без географических данных, отражающих условия и ресурсы производства, на современном этапе развития общества не могут обходиться сельское, лесное, рыбное, охотничье хозяйства, горнодобывающая промышленность, транспорт, строительство и др. Этим отраслям для нормального функционирования необходима оценка благоприятных и неблагоприятных воздействий среды, характеристика многочисленных природных параметров, таких как: морфометрические характеристики рельефа, анализ запасов и прирост естественных ресурсов, их качество, расположение, метеорологические данные, гидрологические данные водных объектов и др. При этом характеристики географических объектов должны давать глубокий анализ процессов происходящих в геосферах, и прогноз их развития, а не носить описательный характер. Содержать в своей основе четкий количественный анализ, дающий оценку, как общему, так и частному состоянию географических объектов, содержать в себе элементы прогнозирования. Сегодня большим спросом пользуется и процесс моделирования, в том числе и природных явлений. Такой метод позволяет не только качественному анализу географических объектов, но и применяется при решении практических задач, например, при постройке гидросооружений. Строительство таких объектов требует получения количественных показателей поведения еще не созданного сооружения на основании поведения его модели. С этой целью была разработана теория подобия. В настоящее время она охватывает процессы движения жидкостей и газов в неразмываемом русле, деформации горных пород, а также теорию термодинамических и электрических моделей. И наша жизнь не стоит на месте. Техногенная цивилизация развивается значительными темпами, растет поток информации, в том числе и географической. На помощь человеку пришли компьютеры. Планета изучается географами не в многолетних опасных плаваниях и путешествиях, а с космических кораблей. Огромное количество промышленных предприятий интенсивно влияет на окружающую среду, географическую оболочку планеты. Чтобы разобраться во всех этих процессах, нужно наблюдать и понимать, как развивается эта большая система природа-человек и как нам надо жить, чтобы все не испортить. И сейчас на помощь географии также приходит математика, только расчеты стали сложнее, а решение находятся гораздо быстрее, ведь у человека в руках столько технических новинок. Значение математики для географии, как одной из составляющих естествознания, очень велико. Математика предопределяет большинство законов природы, являясь универсальным языком, помогающим исследовать не только географическую оболочку, но и целую Вселенную. Именно зародившиеся в математике, как фундаментальной науке, системы различных методов помогают развитию географии в различных направлениях. Применение математических методов в географии огромно, что и было представлено в вышеуказанных примерах. Математика – это наука, помогающая другим научным дисциплинам. Математика – это язык развития предметных дисциплин естествознания. Математика – это скопление методов исследования различных наук. Математика применяется всеми естественными науками в большей мере. Математика взаимосвязана с географией, что и было доказано в нашей работе. Гудкова Н.А., Шифельбейн С.В. В  заимосвязь математики и географии заимосвязь математики и географии Структура взаимосвязей обучающих задач в математике и географии 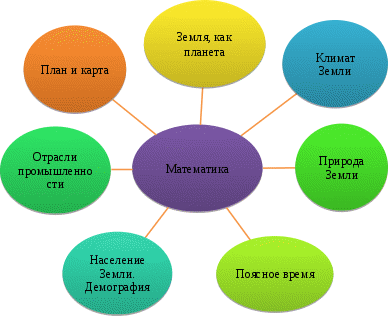 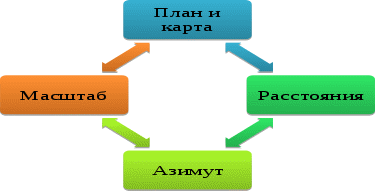 П П лан и карта лан и картаЗадачи по теме «Масштаб» В заданиях 1-3 выберите правильный ответ: 1) Если численный масштаб указан 1:100 000, то это означает что: а) в 1 см – 100 000 км; б) в 1 см – 1 000 км; в) в 1 см 1 км. 2) Если именованный масштаб – в 1 см 50 км, то численный масштаб будет: а) 1:50; б) 1:500 000; в) 1:5 000 000. 3) Переведите именованный масштаб в численный: а) в 1 см – 20 км; б) в 1 см – 150 км; в) в 1 см – 2 км; г) в 1 см – 18 м. Решите задачи 4-5: 4) Длина железнодорожной магистрали 3140 км. Какой длины получится линия, изображающая эту магистраль на карте, сделанной в масштабе 1:10 000 000; 1:2 000000. 5) Чему будет соответствовать на местности расстояние 2 мм на карте масштаба 1: 50 000? Задачи по теме «Азимут» В заданиях 6-8 выберите правильный ответ: Какой стороне горизонта соответствует азимут в 270° ? а) север; б) юг; в) запад; г) восток. 7) Какому азимуту соответствует направление на юго-восток? а)45° б) 135° в)225° г)315°. 8) Группа туристов двигалась сначала по азимуту90°. Затем их дорога свернула вправо на 45°. В каком направлении пошли туристы? а) Ю-В; б) С-В; в) С-З; г) Ю-З. Решите задачи 9-10: 9) Нарисуйте фигуру в масштабе 1: 10000 (в 1 см -100м), используя следующие данные: а) направление (Н)-СВ, расстояние (Р) = 300м, азимут(А)= ? б) Н-ЮВ, Р=300м, А= ? в) Н - З, Р=400м, А= ? г) Н - Ю, Р=500м, А= ? д) Н - В, Р=400м, А= ? е) Н-С, Р=500м, А= ? 10) Туристы наметили такой маршрут: из пункта А, 35°с.ш. решили пойти на север 555 км, затем на восток – 555 км, потом на юг – 555 км и далее на запад – 555 км. Вопрос: вернутся ли туристы в пункт А? Задачи на определение расстояний по карте при помощи линейки, градусной сетки, циркуля, курвиметра Для решения задач 11 – 13используйте карту (рисунок 1). 1 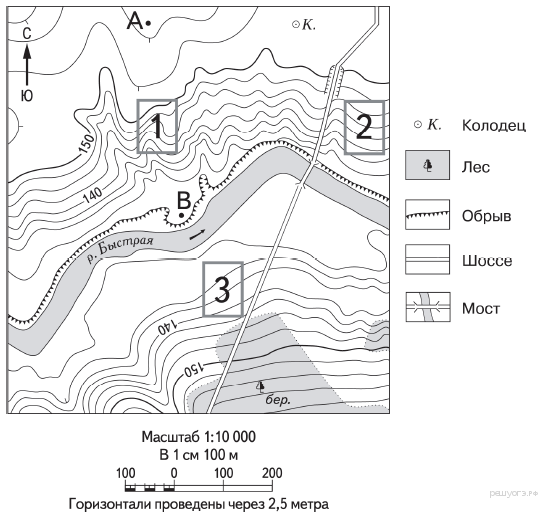 1) Масштаб карты 1:10000 или в 1 см 100 м; размах циркуля – 4 мм. Определите длину реки. 1) Масштаб карты 1:10000 или в 1 см 100 м; размах циркуля – 4 мм. Определите длину реки.При помощи линейки определите расстояние от точки А до точки В. В квадрате километровой сетки помещается 20 делений шкалы курвиметра. Какой длины будет ручеек, если на курвиметре 16 делений. Рис. 1. Топографический план Определить расстояние между городами Вашингтон (75°з.д.) и Анкара (33°в.д.) в градусах и километрах (оба города расположены ближе к 40°с.ш., где 1° равен примерно 85,4 км). Определить расстояние в градусах и километрах между крайними южной (м. Игольный) и северной (м. Рас-Энгела) точками Африки. З  емля как планета емля как планетаДля решения задач 16-19 используй данные из таблиц 1, 2. Таблица 1. Угловая скорость вращения Земли вокруг своей оси
Таблица 2
В том месте в Северном полушарии, где находится корабль, Солнце находится в полдень под углом 53,5º. В этот же день Солнце находится в зените над параллелью 12.3ºс.ш. На какой широте находится корабль? Определите координаты пункта, если известно, что он находится в северном полушарии, высота Солнца над горизонтом 58°20´, дата – 22 июня. Определить координаты пункта, если известно, что пункт расположен в северном полушарии. Когда Солнце стоит в зените на 13°с.ш., в этом пункте высота Солнца над горизонтом 58°20´. Местное время отстает от местного времени г.Москва (долгота 37°30´в.д.) на 16 мин 20 сек. Географические координаты точек А, Б, В и Г показаны в таблице 2. Определите, в какой из точек 1 августа Солнце будет находиться выше всего над горизонтом в 8 часов по солнечному времени Гринвичского меридиана. Ход ваших рассуждений запишите. Используя карту на рисунке 2 определите, в какой из точек, обозначенных буквами на карте, 10 мая Солнце раньше всего по времени Г 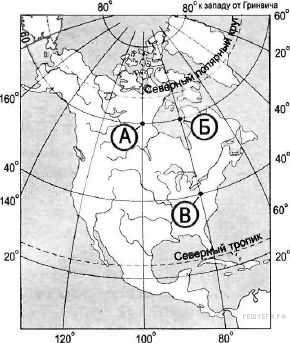 ринвичского меридиана поднимется над горизонтом. Запишите обоснование вашего ответа. ринвичского меридиана поднимется над горизонтом. Запишите обоснование вашего ответа.Рисунок 2 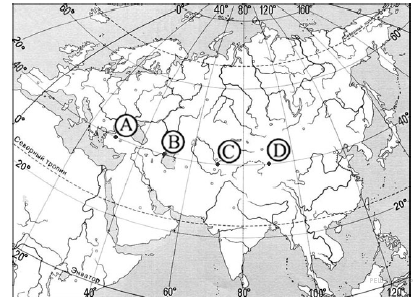 Используя карту на рисунке 3, определите, в каком из пунктов, обозначенных буквами на карте Евразии, 1 августа Солнце будет находиться выше всего над горизонтом в 7 часов по солнечному времени Гринвичского меридиана. Ход ваших рас- Рисунок 3 суждений запишите. П  рирода Земли рирода ЗемлиРешите задачи 22-28: Вычислите температуру в шахте, если на поверхности Земли t = +8˚С, а глубина шахты 750 м. Определите глубину шахты, если температура у поверхности + 24˚ С, а на глубине + 34˚С. Определить падение и уклон реки Волга, если известно, что длина реки равна 3531 км. Вычислить уклон реки Лена на отрезке от устья Витима до устья Олекмы при длине отрезка 627 км. Вычислите, на какой высоте находится исток Енисея, если его уклон составляет 37 см/км. Сколько граммов соли различных веществ можно получить из 1 тонны черноморской воды, если ее соленость 18 промилле? Во сколько раз меньше будет ее количество, чем из 1 тонны воды Красного моря, соленость которого 42 промилле? Используя данные таблицы 3, постройте график изменения температуры вод Мирового океана. Какой вывод можно сделать? Таблица 3. Изменение температуры вод Мирового океана с глубиной
П  оясное время оясное времяРешите задачи 29-37: Определите время в Якутске и в Магадане, если в Москве 12.00 часов. Определите местное время на 30 в.д. и 30 з.д., если на нулевом меридиане 12.00 часов. Определите, когда по московскому времени должен совершить посадку самолет в Ростове-на- Дону (II часовой пояс), вылетевший из Якутска (VIII часовой пояс) в 12 часов по местному времени, если расчетное время полета составляет 8 часов. Иван из Брянска (2-й часовой пояс) хочет поздравить своего друга из Южно-Сахалинска (10-й часовой пояс) с Новым годом ровно в полночь по времени Южно-Сахалинска. Во сколько он должен звонить по времени Брянска? Определите местное время в городах Санкт-Петербург, Владивосток, Тула, Новосибирск и Калининград, если в Москве 12 часов 00 минут. Все расчёты запишите в тетрадь. Определите поясное время в Омске, Москве, Норильске, Анадыре и Екатеринбурге, если в Красноярске 19 часов 15 минут. Рассчитайте поясное время в городе Якутске при условии, что в Ярославле поясное время равно 10.00 часов. Определите время во Владивостоке, если в Москве 12.00 часов. Определите поясное время в Хабаровске, если в Челябинске 07.00 часов. К  лимат Земли лимат Земли 7.1. Температура Решите задачи 38-46: На какую высоты поднялся самолет, если за его бортом температура - 30˚С, а у поверхности Земли + 12˚С? Какова высота горы, если у ее подножья температура + 26˚С, а на вершине - 10˚С? Какова температура воздуха на Памире, если в июле у подножья она составляет + 36˚С, высота Памира 6 км. На высоте 8 км температура равна -18˚С. Какова в это время температура у поверхности? Рассчитайте примерную температуру воздуха за бортом самолета, летящего на высоте 10500м, если температура воздуха у земной поверхности +20˚С. Будет ли лежать снег на вершине: а) горы Килиманджаро (высота5895 м), если температура воздуха у ее подножья + 25˚С; б) горы Косцюшко Большого Водораздельного хребта (2228 м), если температура воздуха у подножья летом +23-25˚С, а зимой -17˚С ? 44) Используя текст учебника (пункт 4, с. 108 «Средние суточные температуры воздуха») и данные задания, вычислите среднюю температуру воздуха:
Определите амплитуду колебания воздуха:
Вычислите среднюю температуру воздуха:
7.2. Атмосферное давление Решите задачи 47-49: 47) Летчик поднялся на высоту 2 км. Каково атмосферное давление воздуха на этой высоте, если у поверхности земли оно равнялось 750 мм рт. ст? 48) На вершине горы высотой 3,5 км барометр показал 720 мм рт. ст. Каково давление у подножья? 49) На дне карьера барометр зафиксировал давление 780 мм рт. ст., у поверхности земли — 760 мм рт. ст. Найти глубину карьера. 7.3. Влажность воздуха Пользуясь данными таблицы 4, решите задачи 50-51:
50) Определи абсолютную влажность воздуха, если относительная влажность при температуре + 20°С равна 50%. 51) 1 м³ воздуха имеет температуру + 10°С и содержит 6 г воды. Является ли такой воздух насыщенным? Население Земли. Демография   Плотность населения Решите задачи 52-54: Численность населения Албании на 01.01.92г. была 3 189 тыс. человек. Площадь – 28,7 тыс. кв. км. За 1992-1997гг. естественный прирост составил 431тыс. человек. Внешняя миграция составила 480 тыс. человек, из них эмигрировало 320 тыс. человек. Внутренняя миграция – 730 тыс. человек. Рассчитать плотность населения Албании за 1997год. Определите численность населения региона, площадь которого 100 тыс. км², если плотность сельского населения в его пределах 20 чел. на 1 км2 и его доля составляет 40% от общей численности (площадью городских поселений пренебречь). Высчитайте плотность населения республики Башкортостан, если площадь – 143 тыс. км², численность населения составляет 4065 тыс. чел. Воспроизводство населения Решите задачи 55-59: Вычислите, на сколько изменится численность населения в стране за год в результате естественного прироста, если на начало года она составила 136 млн. чел., а естественный прирост населения составил 5,6‰. Как изменится за год численность населения города, если в начале года в нем проживало 500тыс. чел., в течение года умерло 12 тыс. чел, а рождаемость составила 10‰. Как изменится за год численность населения города, если в начале года в нем проживало 3500тыс. чел., рождаемость составила 10‰, а смертность – 8‰ ? Используя данные таблицы 5, определите показатель естественного прироста населения (в ‰) в 2011 г. для Пермского края. При расчётах используйте показатель среднегодовой численности населения. Запишите решение задачи. Полученный результат округлите до десятых долей промилле. Таблица 5. Численность и естественный прирост населения Пермского края
Пользуясь данными таблицы 6, рассчитайте показатель естественного прироста населения за год одной из африканских стран. Таблица 6
Миграционные процессы Рассчитайте сальдо миграции за год, если в начале года в стране проживали 10 млн. человек, в конце года – 11,5 млн. человек, а естественный прирост за год составил 250 тыс. человек. Определите величину годового естественного прироста населения, если в начале года в стране проживали 6 млн. человек, в конце года – 6,2млн. человек, а миграционная убыль составила 40 тыс. человек. Найдите годовое сальдо миграции, если в начале года в стране проживали 7млн. чел., в конце года – 8,5млн. чел., а естественный прирост населения за год составил 26‰. Рассчитайте, как изменится численность населения в городе, если за год рождаемость составила 600 человек, смертность 800 человек, количество выбывших – 1200 человек, количество прибывших – 700. Определите численность населения города на конец года, если в начале года в нем проживало 50 000 человек, естественный прирост за год составил 20‰, а сальдо миграции +2 800 человек. О  трасли хозяйства трасли хозяйстваРешите задачи 65-73: 65) Металлургический комбинат имеет годовую мощность 200 тыс. т чугуна. Определите, какими должны быть разведанные запасы месторождения железной руды, чтобы обеспечить работу этого комбината в течение ближайших 30 лет при следующих условиях: а) при добыче и обогащении теряется 25% руды; б) содержание железа в руде достигает 40 %. 66) Оскольский металлургический комбинат имеет мощность 3,5 млн. т стали. Какое количество железной руды (с содержанием железа 40%)приходится завозить на комбинат? 67) Определите, какое количество условного топлива позволяет сэкономить за год Ленинградская АЭС мощностью 4 млн. кВт при удельном расходе топлива на 1 кВт/ч в 320 г у. т. Стоимость топлива 2 руб. за 1 кг у. т. Время работы электростанции за год 6800 часов. 68) Какой мощности должна быть ТЭС, заменившая Чернобыльскую АЭС, если ее мощность – 3 млн. кВт, а время работы ее в течение года составила 7000 ч, а время работы ТЭС – 6000 ч. Удельный расход топлива на 1 кВт/ч электроэнергии – 333год. 69) Рассчитайте, с какой площади необходимо собрать подсолнечник, чтобы произвести 20 т масла, то есть такое её количество, которое добывают из одного синего кита. Взять средний урожай подсолнечника 12 ц с гектара и предположить, что выход масла составляет 36%. 70) В течение рабочего дня человек может выровнять 200 м² земли, а при помощи бульдозера за это время можно выровнять площадь в 6 га. Сколько рабочих заменит бульдозер? 71) Выбрав необходимые данные из таблицы 7, определите ресурсообеспеченность Саудовской Аравии нефтью. Таблица 7
72) Канавокопательная машина за рабочий день – 7 часов выкапывает канаву глубиной 2 м, шириной 80 см и длиной 120 м. сколько кубических метров земли выбрасывает канавокопательная машина в среднем за 1 час? Сколько землекопов заменяет такая машина, если норма на одного землекопа в день в мягком грунте составляет 4 м³? Высчитайте с точностью до 1 тонны массу грунта. Который вырыли землекопы при строительстве оборонительного рва на Красной площади, если известно, что ров был длиной 541,2 м, глубиной – 8,5 м, шириной – 36,4 м, а масса 1 куб. грунта – 2,5 т. З  адачи повышенного уровня сложности адачи повышенного уровня сложностиРешите задачи 73 - 91: Поднятие Карпат происходит со скоростью 1-2см в год. Сколько лет понадобилось горам, чтобы достичь теперешней высоты? Разница во времени между крайними западной и восточной точками Украины составляет 1час 12минут. Докажите математически, какое расстояние по градусной сетке между этими точками. Западная точка – ст. Чоп – 22о08` в.д.; Восточная точка – Красная Звезда – 40о13` в.д. Расстояние между двумя селами на плане, масштаб которого 1:300 000, составляет 22см. Каким будет это расстояние на плане с масштабом. Москва и Аддис-Аббеба находятся на одном меридиане. Определите расстояние между ними. 1о дуги меридиана соответствует 111км. Определите расстояние между двумя столицами: Украины и Египта в градусах и километрах, используя только картографическую сетку. В каком городе и на сколько минут Солнце восходит раньше – в Харькове или во Львове. Объясните свои расчеты. В каком городе и на сколько минут Солнце заходит позднее – в Киеве или во Львове. Объяснить свои расчеты. Определить площадь острова Рудольфа, который расположен между 81,7о и 81,9о с.ш. и 58о и 59,2о в.д. Форма острова почти прямоугольная. Площадь основных водохранилищ Украины равна 7400 км2. Определите, какую часть они занимают от всей площади Украины. Плодовый сад на плане 1:10000 имеет форму прямоугольника со сторонами 97 мм и 63,5 мм. Определите площадь сада на местности. Расстояние по экватору от нулевого до десятого меридиана по карте мира составляет 5см. Определите масштаб карты. Записать его в виде числового и именованного. Расстояние между двумя селами на плане, масштаб которого 1:400000, составляет 17см. Каким будет это расстояние на плане с масштабом. Точка А в Африке расположена ниже уровня океана на 133м, а относительная высота между точками 6028м. Определите абсолютную высоту точки В. назовите эти точки Африки. Самолет вылетел с места, координаты которого 50 с.ш. 30 в.д., и приземлился в месте с координатами 60 с.ш. и 30 в.д. Определите расстояние между местами вылета и приземлением самолета. Территория смешанного леса на плане масштаба 1:5000 имеет форму прямоугольника со сторонами 4,5 и 6 см. А хвойный лес на плане масштаба 1:2500 имеет форму квадрата со сторонами 8 см. Какой лес - смешанный или хвойный - имеет на местности большую площадь и на сколько? Вычислите высоту одного из крупнейших барханов Западной Сахары, если известно, что крутизна его подветренного склона 30°, а длина - 200 м. Определите среднюю ширину бассейна Амазонки, если его площадь равна 7,2 млн км2, а длина - 6,5 тыс. км. Определите, как изменится уровень Мирового океана, когда растает лед толщиной 3,5 м на площади 55 млн км2. На карте с масштабом 1:10 000 площадь острова 2 кв.см. Какова площадь данного острова в действительности? Измерив, расстояние от Москвы до Благовещенска по карте и, используя масштаб, вычислить расстояние между данными городами. Приняв скорость движения самолета в 720 км/ч, определить время его полета. Вычислите площадь Скородома, зная, что суммарная площадь трех указанных частей Москвы составляет 625/1878 от площади столицы в границах Скородома. Д  ля души: старинные задачи ля души: старинные задачи Решите задачи 92 - 105: Из 3 снопов хорошего урожая, 2 снопов среднего урожая и 1 снопа плохого урожая получили 39 доу (доу — мера объема) зерна. Из 2 снопов хорошего урожая, 3 снопов среднего урожая и 1 снопа плохого урожая получили 34 доу зерна. Из 1 снопа хорошего урожая, 2 снопов среднего урожая и 3 снопов плохого урожая получили 26 доу зерна. Спрашивается, сколько зерна получили из каждого снопа хорошего, среднего и плохого урожая (задача из «Математики в девяти книгах»). 1 петух стоит 5 цяней (цянь — денежная единица), 1 курица стоит 3 цяня, 3 цыпленка стоят 1 цянь. Всего на 100 цяней купили 100 птиц. Спрашивается, сколько было в отдельности петухов, кур, цыплят (задача Чжан Цюцзяня). Найти число павлинов в стае, 1/16 которой, умноженная на себя, сидит на манговом дереве, а квадрат 1/9 остатка вместе с 14 другими павлинами — на дереве тамала (задачи Магавиры). О друг, назови число различных ожерелий, которые можно получить из бриллиантов, сапфиров, изумрудов, кораллов и жемчугов (задачи Магавиры). Стая голубей подлетела к высокому дереву. Часть голубей села на ветвях, а другая расположилась под деревом. Сидевшие на ветвях голуби говорят расположившимся внизу: «Если бы один из вас взлетел к нам, то вас стало бы втрое меньше, чем нас всех вместе, а если бы один из нас слетел к вам, то нас с вами стало бы поровну». Сколько голубей сидело на ветвях и сколько под деревом? (Задача из сказки «1001 ночь» (ночь 458-я). Плата работнику за месяц, то есть за тридцать дней,— десять динаров и платье. Он работал три дня и заработал платье. Какова стоимость платья (задача ал-Каши). Трое хотят купить дом за 2400 ливров. Они условились, что первый даст половину, второй — одну треть, а третий — оставшуюся часть. Сколько даст каждый? (задача Жака Озанама). На трех лугах площадью 31/3 , 10 и 24 га трава растет одинаково, т. е. с одинаковой густотой и с одним и тем же приростом. После того как на первом лугу 12 коров паслись 4 недели, а на втором лугу 21 корова паслась 9 недель, трава оказалась съеденной настолько, что оба пастбища на время пришлось забросить. Сколько коров можно пасти на третьем лугу в течение 18 недель? ( задача Исаака Ньютона). Летела стая гусей, навстречу им один гусь и рече: «Бог в помочь летети сту гусям». И гуси ему сказали: «Не сто нас гусей всей стаей летит: нас летит стая и как бы и нам еще столько, да полстолько, да четверть столько, да ты, гусь, и то было б сто гусей» (задача из рукописи XVI в). Артели косцов надо было скосить два луга, один вдвое больше другого. Половину дня артель косила большой луг. После этого артель разделилась пополам: первая половина осталась на большом лугу и докосила его к вечеру до конца; вторая же половина косила малый луг, на котором к вечеру еще остался участок, скошенный на другой день одним косцом за один день работы. Сколько косцов было в артели? (задача Л.Н. Толстого). В XV в. суммарная площадь Пскова, Великого Новгорода и Нижнего Новгорода составляла 940 га, из которых 11/47 приходилась на долю Пскова. Вычислите площадь каждого из городов, если известно, что Нижний Новгород занимал территорию на 100 га меньшую, чем Новгород Великий (Перли С.С.). Из под земли бьют четыре источника. Первый заполняет бассейн за один день,- второй- за два дня, третий- за четыре дня. Сколько времени наполнят бассейн все четыре источника вместе? (Герона Александрийского). Есть кадамба цветок. На один лепесток пчелок пятая часть опустилась. Рядом тут же росла вся а цвету сименгда, И на ней третья часть поместилась. Разность их ты найди, трижды их ты сложи, На кутай этих пчел посади. Лишь одна не нашла себе места нигде, Все летала то взад, то вперед И везде ароматом цветов наслаждалась. Назови теперь мне, подсчитавши в уме, Сколько пчелок всего здесь собралось? (Древнеиндийская задача.) Из множества цветков чистых цветков лотоса были принесены в жертву: Шиве – третью долю этого множества, Вишпу – пятую, Солнцу шестую, четвёртую долю получил Бхавани, а остальные шесть цветков получил уважаемый учитель. Сколько было цветков? Площадь Китай-города была на 39 га больше площади Кремля. Площадь Белого города – на 467,5 га больше площади Китай-города. Причем площади Белого города и Кремля, вместе составляли 559,5 га (Перли С.С.). Вычислите площадь Скородома, зная, что суммарная площадь трех указанных частей Москвы составляет 625/1878 от площади столицы в границах Скородома. Заключение В данном сборнике на примере конкретных задач представлены доказательства тому, что математика и география науки неразрывно связаны друг с другом. И сегодня, в наше высокотехнологичное время, география и математика продолжают совместно работать на благо человечества. Если бы математика тесно не сотрудничала с географией, география вообще как наука не смогла бы развиваться. Доказательствами к этому являются такие факты: 1 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
