ТРЗ диф исчисление. ТРЗ. Дифференциальное исчисление функции одной переменной.. Сборник задач по высшей математике РостовнаДону 2002 г. Составитель Л. В. Сахарова удк 517 с 221
 Скачать 1.3 Mb. Скачать 1.3 Mb.
|
|
Министерство транспорта РФ Филиал Новороссийской государственной морской академии в г. Ростове-на-Дону Введение в анализ. Дифференциальное исчисление функций одной переменной Сборник задач по высшей математике Ростов-на-Дону 2002 г. Составитель Л.В. Сахарова УДК 517 С 221 Введение в анализ. Дифференциальное исчисление функций одной переменной: Сборник задач по высшей математике. Ростов-на-Дону: Типография ООО "ВУД", 2002.- с. Пособие предназначено для проведения занятий по курсу высшей математики и организации самостоятельной работы курсантов. Может быть использовано для составления вариантов типового расчётного задания. Печатается по решению общенаучной кафедры филиала НГМА в г. Ростове-на-Дону Рецензент: начальник общенаучной кафедры филиала НГМА, доцент, к.ф.-м.н. Н.Ю.Сафонцева Типография ООО "ВУД", 2002 §1. Функциональная зависимость 1.1. Дано: 1.2. Дано: 1.3. Дано:  . Найти: f(–1); f(1); f(0); . Найти: f(–1); f(1); f(0); 1.4. Дано: Найти: 1.5. Доказать, что функция 1.6. Доказать, что функция 1.7. Дано: 1) 2) 1.8. Дано: 1.9. Дано: 1.10. Дано: 1.11. Найти области определения следующих функций: 1) 3) 5) 7) 9) 11) 13) 15) 1.12. Записать в явном виде функцию y, заданную неявно: 1) 3) 5) 7) 1.13. Из уравнений, параметрически задающих функцию, исключить параметр: 1) 3) 5) 1.14. Выяснить, какие из следующих функций являются чётными, нечётными, какие не являются ни чётными, ни нечётными: 1) 3) 5) 7) 9) 11) 1.15. Для данных функций найти им обратные: 1) 3) 5) 7) 9) 11) 1.16. Какие из следующих функций являются периодическими: 1) 3) 5) 7) 9) §2. Пределы В задачах 2.1–2.64 вычислить пределы: 2.1. 2.3. 2.5. 2.7. 2.9.  . .2.11. 2.13. 2.15. 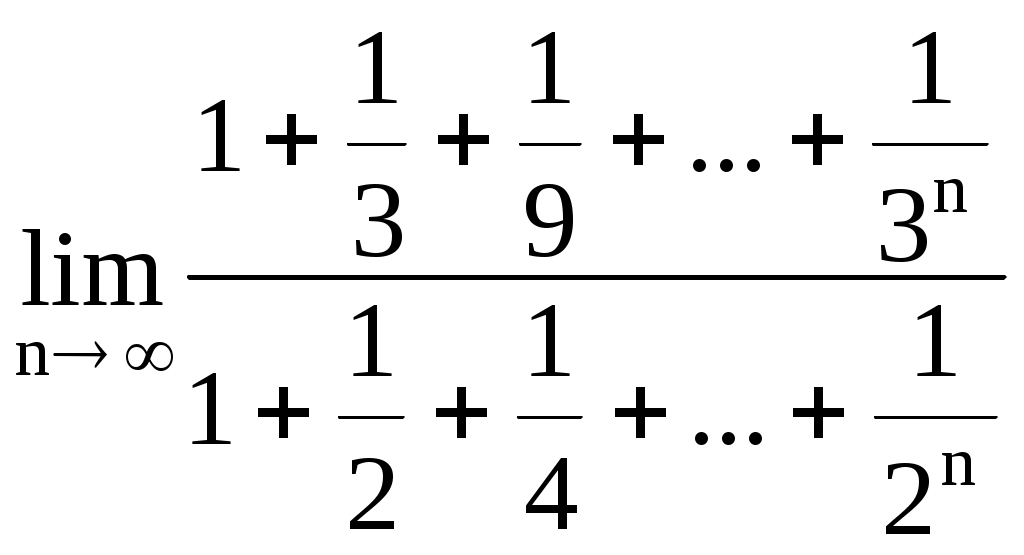 . 2.16. . 2.16. 2.17. 2.19.  . .2.21. 2.23. 2.25. 2.27. 2.29. 2.31. 2.33. 2.35. 2.37.  . 2.38. . 2.38.  . .2.39. 2.41. 2.43. 2.45. 2.47. 2.49. 2.51. 2.53. 2.55. 2.57. 2.59. 2.61. 2.63. В задачах 2.65–2.134 вычислить пределы функций, используя спецпределы: 2.65. 2.67.  . .2.69. 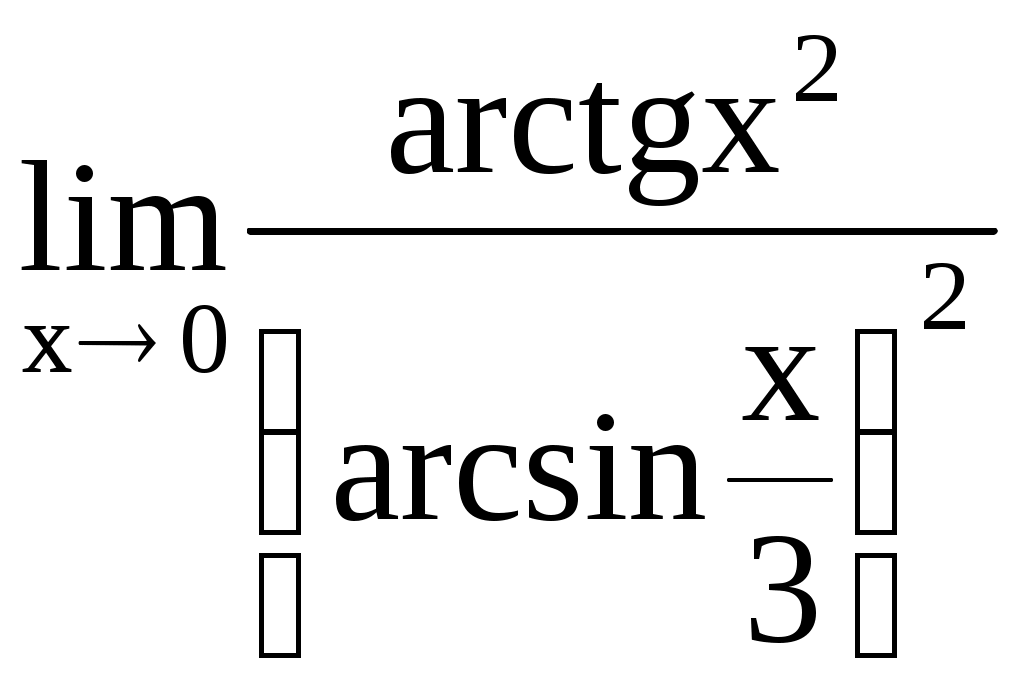 . .2.71. 2.73. 2.75. 2.77. 2.79. 2.81.  . .2.83.  . 2.84. . 2.84. 2.85. 2.87.  . 2.88. . 2.88. 2.89. 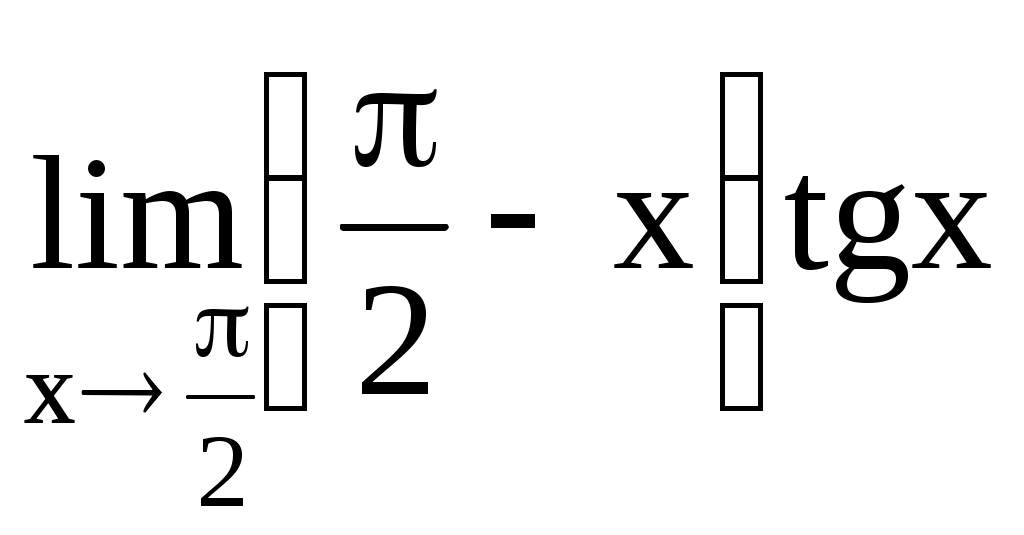 . 2.90. . 2.90. 2.91. 2.93. 2.95. 2.97. 2.99. 2.101. 2.103. 2.105. 2.107. 2.109. 2.111. 2.113. 2.115. 2.117. 2.118. 2.119. 2.120.  . .2.121. 2.123. 2.125.  . 2.126. . 2.126. 2.127. 2.129. 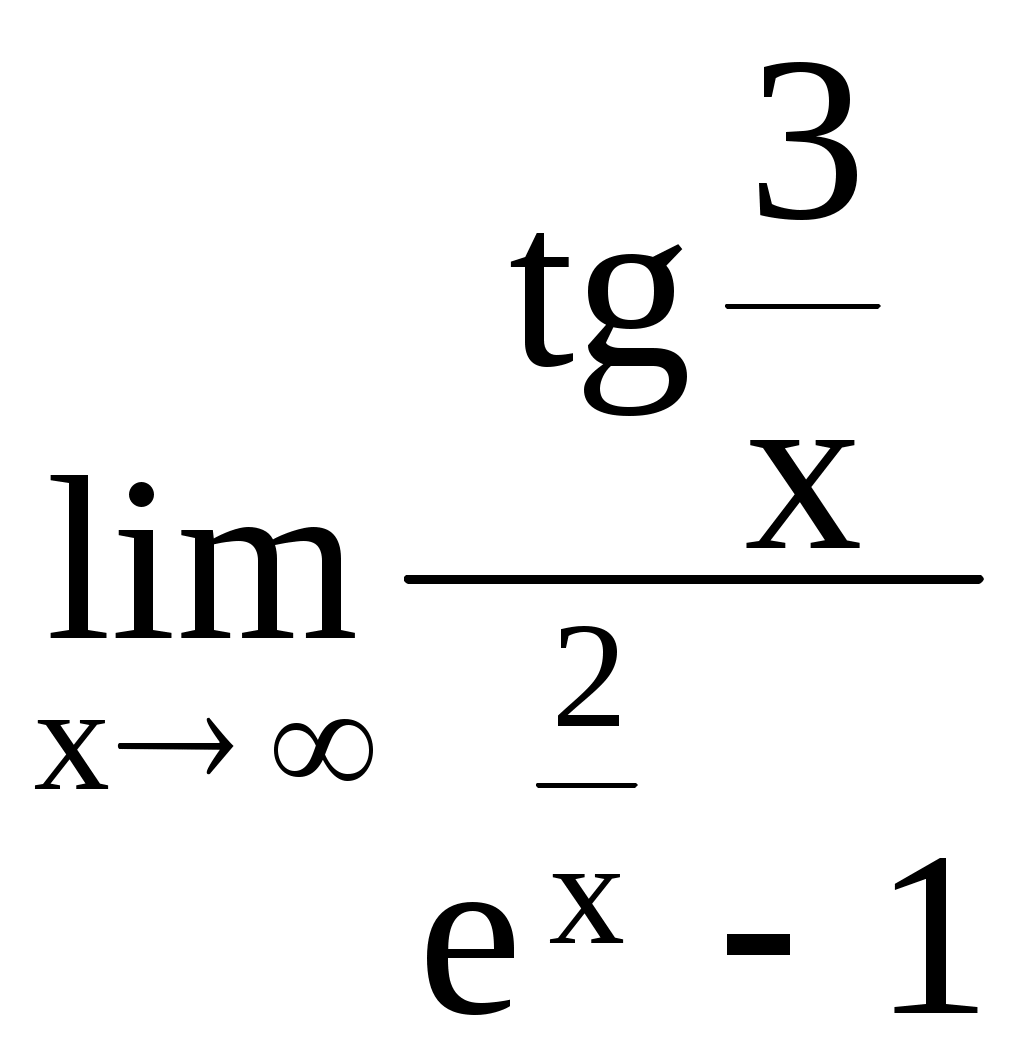 . 2.130. . 2.130. 2.131.  . .2.133. Вычислить односторонние пределы функций: 2.135. 2.137.  . .2.139. 2.141. Сравнить функции и , бесконечно малые при х0: 2.142. 2.143. 2.144. 2.145. 2.146. 2.147. 2.148. |
