ексел 4е. Методичка_7 Excel Приближенное вычисление функции. Семинара по компьютерному практикуму Электронное издание Москва 2017 Введение
 Скачать 1.01 Mb. Скачать 1.01 Mb.
|
 Федеральное государственное образовательное бюджетное учреждение высшего образования «ФИНАНСОВЫЙ УНИВЕРСИТЕТ ПРИ ПРАВИТЕЛЬСТВЕ РОССИЙСКОЙ ФЕДЕРАЦИИ» Департамент анализа данных, принятия решений и финансовых технологий Д.В.Берзин Приближенное вычисление функции через разложение по формуле Тейлора/Маклорена Учебно-методические рекомендации для проведения семинара по компьютерному практикуму Электронное издание Москва 2017 Введение Напомним, что рядом Тейлора функции 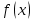 в точке в точке 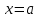 называется называется степенной ряд 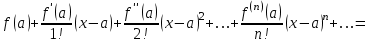 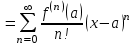 (1) (1)В частном случае при 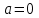 ряд (1) называется рядом Маклорена: ряд (1) называется рядом Маклорена: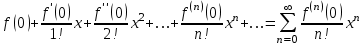 (2) (2)Частичная сумма ряда  является многочленом (полиномом) n-й степени, который приближает (аппроксимирует) исходную функцию f(x) в окрестности нуля. Из курса математического анализа известно, что чем выше степень n многочлена, тем ближе он приближается к исходной функции (т.е. тем ниже погрешность приближения). является многочленом (полиномом) n-й степени, который приближает (аппроксимирует) исходную функцию f(x) в окрестности нуля. Из курса математического анализа известно, что чем выше степень n многочлена, тем ближе он приближается к исходной функции (т.е. тем ниже погрешность приближения).Пример Рассмотрим хорошо известную из школьного курса математики функцию f(x) = sin(x). Для этой функции 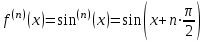 , , 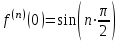 , , 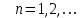 . .Отсюда следует, что при x=0 производные четного порядка равны нулю, а производные нечетного порядка чередуют знак с плюса на минус. По формуле (2) составим ряд Маклорена: 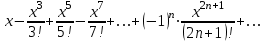 . .Приблизим f(x) = sin(x) в окрестности нуля многочленом 1-й степени 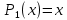 . Создадим книгу MS Excel «Маклорен», и на отдельном листе (назовем его «Линейная») заполним три столбца. Первый из них – это значения аргумента (скажем, с шагом 0,1 на интервале [-2,2]), второй столбец – это соответствующие значения функции «синус», вычисляемые посредством встроенной функции MS Excel “SIN”, а третий столбец – соответствующие значения тождественной линейной функции f(x)=x. Введя формулу в ячейку верхнего ряда, растягиваем значения по столбцу вниз, тем самым быстро заполняя все ячейки столбца (техника «drag and drop», т.е. «потяни и отпусти» - одна из фундаментальных и очень полезных особенностей MS Excel). Выделив все три столбца и применив ВСТАВКА->ДИАГРАММА->ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ, получим изображение двух графиков в одних и тех же осях: синим цветом y=sin(x) и оранжевым цветом . Создадим книгу MS Excel «Маклорен», и на отдельном листе (назовем его «Линейная») заполним три столбца. Первый из них – это значения аргумента (скажем, с шагом 0,1 на интервале [-2,2]), второй столбец – это соответствующие значения функции «синус», вычисляемые посредством встроенной функции MS Excel “SIN”, а третий столбец – соответствующие значения тождественной линейной функции f(x)=x. Введя формулу в ячейку верхнего ряда, растягиваем значения по столбцу вниз, тем самым быстро заполняя все ячейки столбца (техника «drag and drop», т.е. «потяни и отпусти» - одна из фундаментальных и очень полезных особенностей MS Excel). Выделив все три столбца и применив ВСТАВКА->ДИАГРАММА->ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ, получим изображение двух графиков в одних и тех же осях: синим цветом y=sin(x) и оранжевым цветом 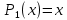 . Видим, что графики сильно различаются, т.е. аппроксимацию назвать хорошей нельзя (см. рис. 1). . Видим, что графики сильно различаются, т.е. аппроксимацию назвать хорошей нельзя (см. рис. 1).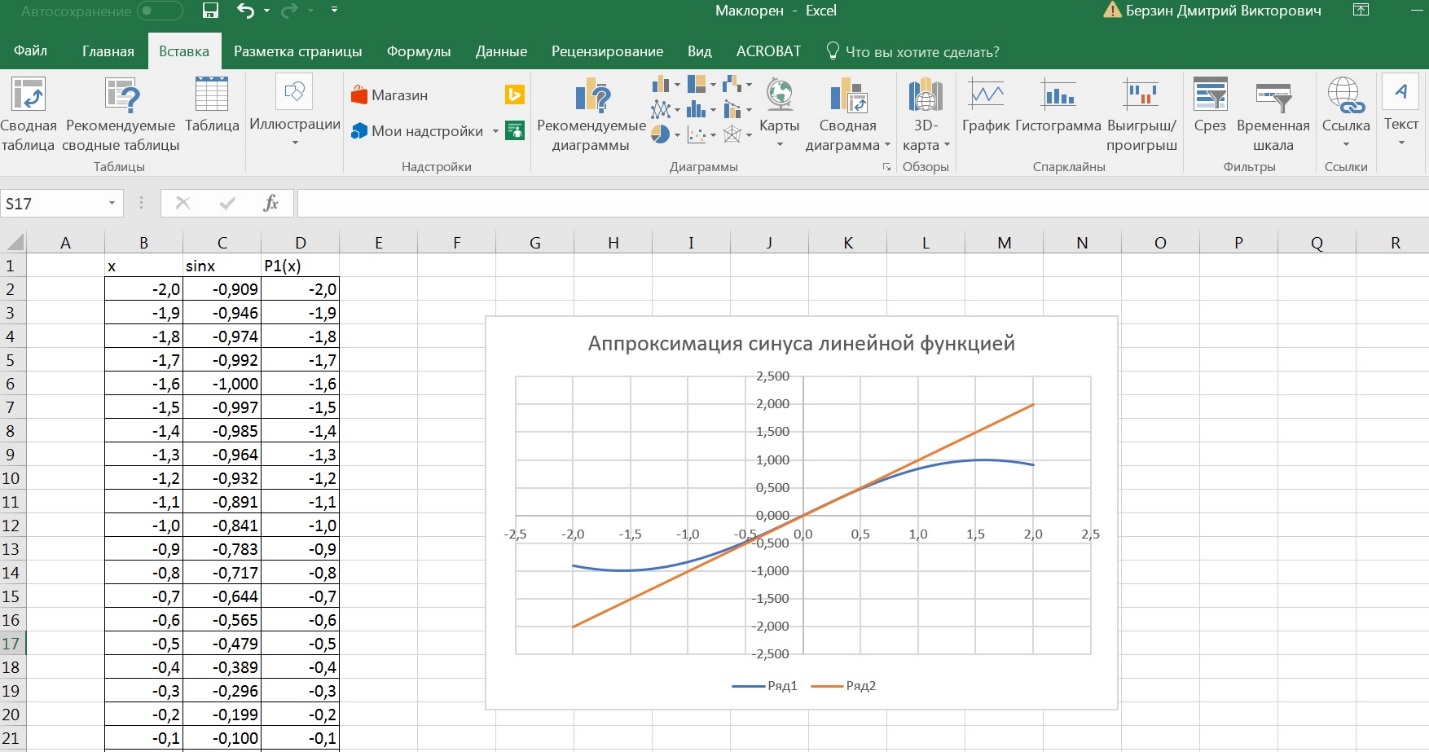 Рис. 1. Аппроксимация синуса линейной функцией. Теперь будем аппроксимировать y=sin(x) в окрестности нулякубическим многочленом 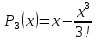 . Создав в этом же файле новый лист «Кубическая» и выполнив действия по той же схеме, что и в листе «Линейная», приходим к рис. 2. . Создав в этом же файле новый лист «Кубическая» и выполнив действия по той же схеме, что и в листе «Линейная», приходим к рис. 2.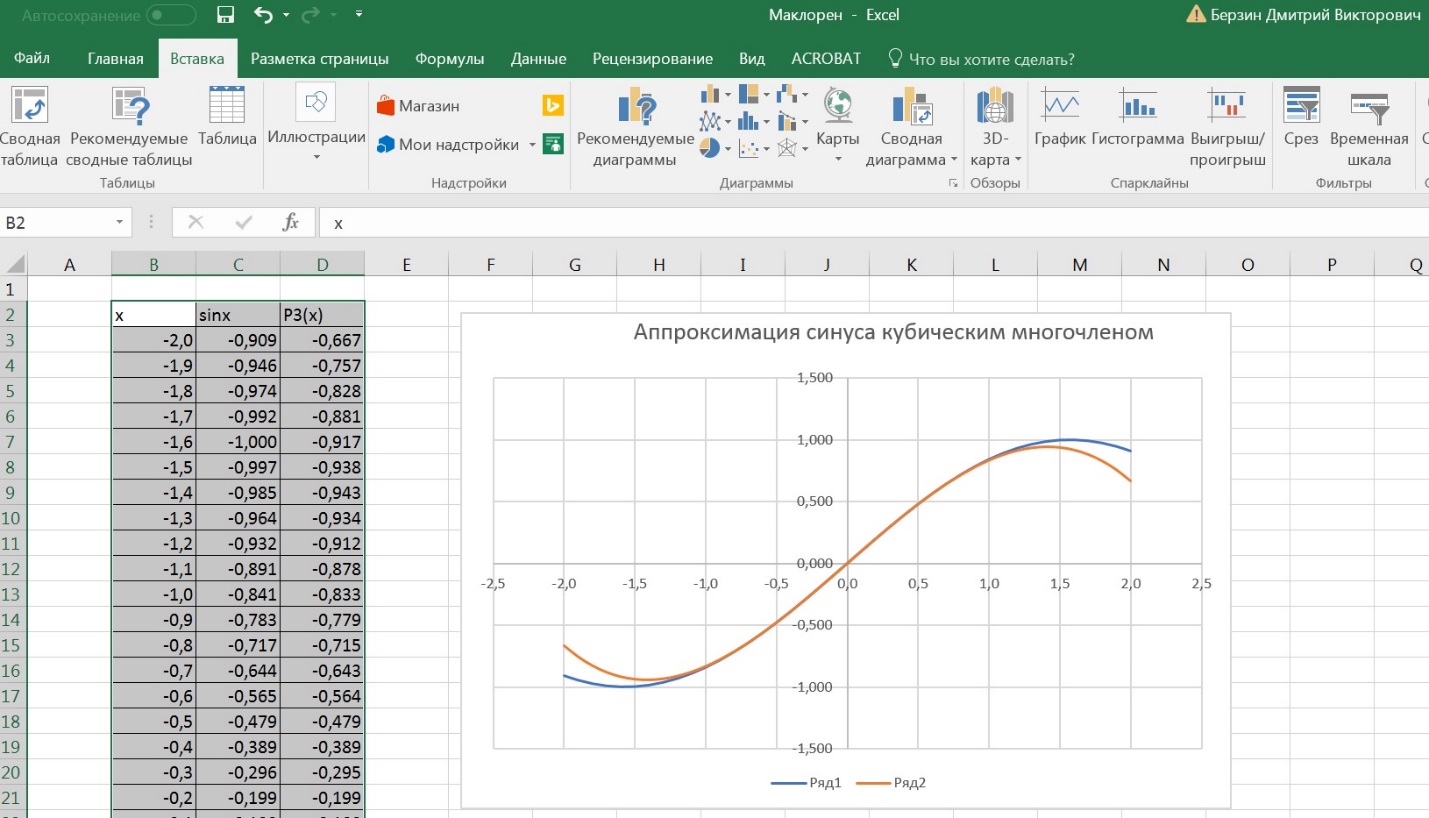 Рис. 2. Аппроксимация синуса кубическим многочленом. Наблюдаем, что аппроксимация теперь значительно лучше, функции заметно разнятся лишь в концах интервала. Наконец, приблизим y=sin(x) в окрестности нулямногочленом 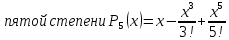 . Создав новый лист «Пятой степени» и выполнив действия аналогично тому, что делалось в предыдущих листах, приходим к результату, изображенному на рис. 3. . Создав новый лист «Пятой степени» и выполнив действия аналогично тому, что делалось в предыдущих листах, приходим к результату, изображенному на рис. 3.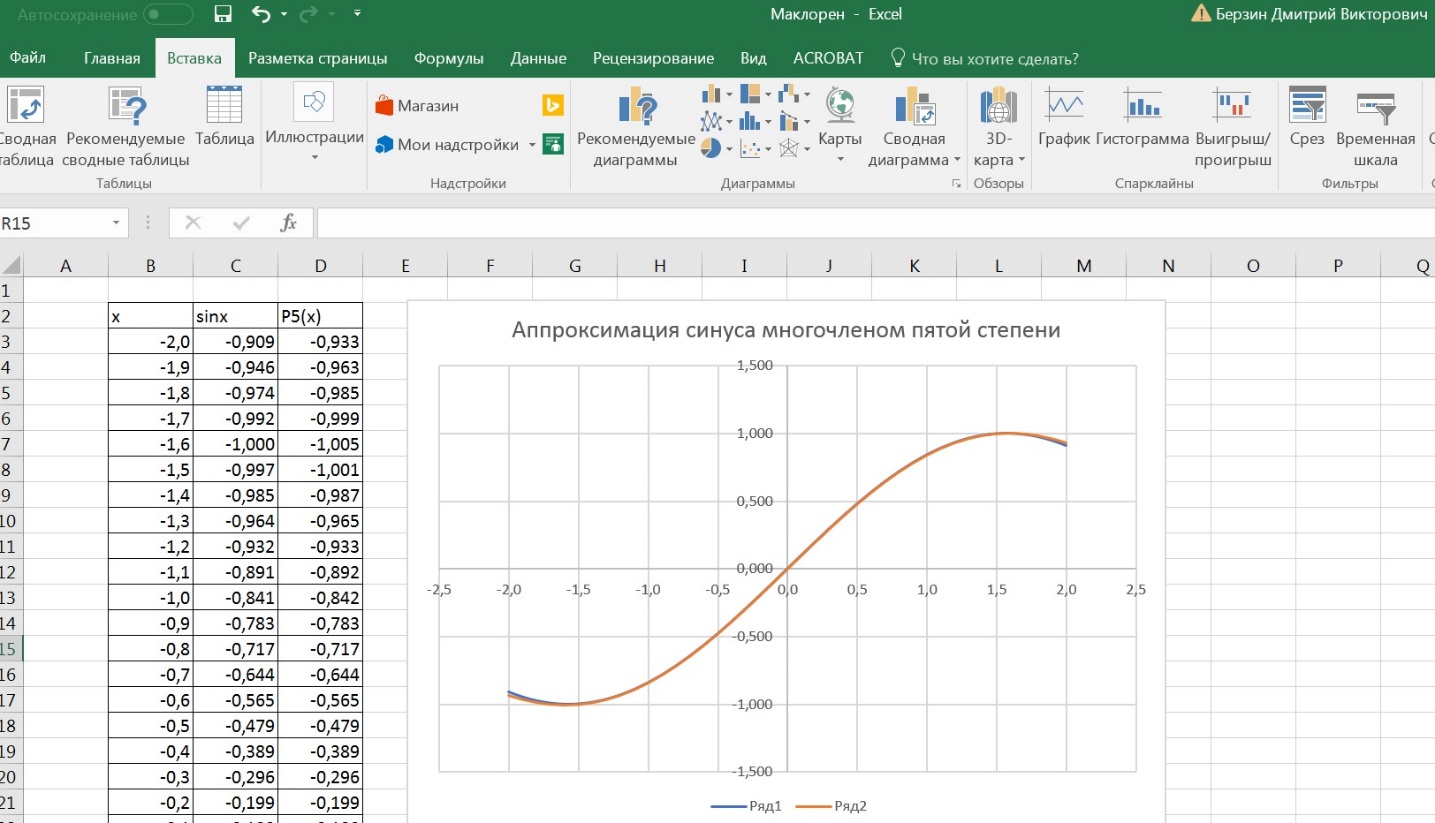 Рис. 3. Аппроксимация синуса многочленом пятой степени. Теперь видим, что аппроксимация – хорошая, в выбранной окрестности нуля функции почти совпадают (едва различаются лишь на концах интервала). Задания для самостоятельной работы Разложить в ряд Маклорена функцию 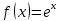 . В MS Excel аппроксимировать эту функцию частичными суммами ряда Маклорена – многочленами 1-й, 2-й, 3-й, 4-й и 5-й степени. Рассмотреть интервалы [-1;1] и [-3;3] и шаги 0,1 и 0,03. На каких интервалах и шагах погрешность аппроксимации визуально наблюдается лучше всего? . В MS Excel аппроксимировать эту функцию частичными суммами ряда Маклорена – многочленами 1-й, 2-й, 3-й, 4-й и 5-й степени. Рассмотреть интервалы [-1;1] и [-3;3] и шаги 0,1 и 0,03. На каких интервалах и шагах погрешность аппроксимации визуально наблюдается лучше всего?Разложить в ряд Маклорена функцию 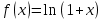 . В MS Excel аппроксимировать эту функцию частичными суммами ряда Маклорена – многочленами 1-й, 2-й, 3-й, 4-й и 5-й степени. Рассмотреть интервал [-0,5;0,5] и шаги 0,05 и 0,01. Какова область сходимости этого ряда? . В MS Excel аппроксимировать эту функцию частичными суммами ряда Маклорена – многочленами 1-й, 2-й, 3-й, 4-й и 5-й степени. Рассмотреть интервал [-0,5;0,5] и шаги 0,05 и 0,01. Какова область сходимости этого ряда?Разложить в ряд Маклорена функцию 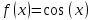 . В MS Excel аппроксимировать эту функцию частичными суммами ряда Маклорена – многочленами 2-й, 4-й, и 6-й степени. Рассмотреть интервал [-4;4] и шаги 0,04 и 0,01. Какова область сходимости этого ряда? . В MS Excel аппроксимировать эту функцию частичными суммами ряда Маклорена – многочленами 2-й, 4-й, и 6-й степени. Рассмотреть интервал [-4;4] и шаги 0,04 и 0,01. Какова область сходимости этого ряда? |
