курсовая. ПКЗ+проектный+подход+в+адм.-госуд.управ. Сетевое планирование и график Гантта Выбрав вариант задания из таблицы 1, соответствующий первой букве фамилии студента или слушателя, выполнить нижеследующее

• Название: Сетевое планирование и график Гантта Выбрав вариант задания из таблицы 1, соответствующий первой букве фамилии студента или слушателя, выполнить нижеследующее
• Анкор: курсовая
• Дата: 24.05.2023
• Размер: 0.59 Mb.
• Имя файла: ПКЗ+проектный+подход+в+адм.-госуд.управ.doc
• Тип: Документы; #1155844

ДЕЛАЕМ 7 ВАРИАНТ

Часть 2. Индивидуальные задания по теме Сетевое планирование и график Гантта

Выбрав вариант задания из таблицы 1, соответствующий первой букве фамилии студента или слушателя, выполнить нижеследующее:

• 
  составить сетевой график работ в виде логической последовательности их выполнения и указать длительность каждой из работ;
  
• 
  рассчитать ранние и поздние сроки наступления событий, ранние и поздние сроки начала и окончания работ, полный и свободный резервы каждой работы. Результаты расчетов занести в таблицу 2;
  
• 
  в результате найти и выделить на графике критический путь, определить время, необходимое на выполнение всех работ;
  
• 
  составить диаграмму Гантта.
  

Таблица 1

Длительность работ

Работа	Номер варианта задания (начальная буква фамилии)
	1	2	3	4	5	6	7	8	9	10
	А, Л, Х	Б, М, Ц	В, Н, Ч	Г, О, Ш	Д, П, Щ	Е(Ё), Р, Э	Ж, С, Ю	З, Т, Я	И, У	К, Ф
(1, 2)	5	6	15	5	10	5	10	7	3	3
(1, 3)	8	10	7	9	3	7	5	16	6	8
(1, 4)	5	4	8	7	7	13	8	5	7	6
(2, 3)	7	3	11	3	10	9	3	4	7	9
(2, 5)	10	12	15	12	8	4	11	6	9	8
(2, 6)	6	7	4	9	5	7	15	8	12	6
(3, 4)	7	8	5	6	5	6	7	10	5	10
(3, 6)	5	9	12	8	7	12	6	11	7	4
(4, 6)	5	5	8	7	9	6	11	10	8	4
(5, 6)	5	11	7	5	15	4	12	5	3	7
(5, 9)	4	4	6	3	8	5	7	3	9	5
(6, 7)	15	11	10	15	3	10	10	4	8	10
(6, 8)	10	8	4	10	7	15	6	8	6	2
(7, 8)	8	3	3	8	6	10	8	6	10	3
(7, 9)	3	5	8	9	12	3	15	7	4	7
(8, 9)	11	2	5	7	10	8	10	9	11	4

Таблица 2

Работа (i,j)	Количество предшествующих работ	Продолжительность tij	Ранние сроки: начало ТijР.Н.	Ранние сроки: окончание tijР.О.	Поздние сроки: начало ТijП.Н.	Поздние сроки: окончание tijП.О.	Резервы времени: полный Rпij	Резервы времени: свободный Rсij
(1,2)		10
(1,3)		5
(1,4)		8
(2,3)		3
(2,5)		11
(2,6)		15
(3,4)		7
(3,6)		6
(4,6)		11
(5,6)		12
(5,9)		7
(6,7)		10
(6,8)		6
(7,8)		8
(7,9)		15
(8,9)		10

Решение:

Резерв времени события показывает, на какой допустимый период времени можно задержать наступление этого события, не вызывая при этом увеличения срока выполнения комплекса работ.

Для определения резервов времени по событиям сети рассчитывают наиболее ранние t^p и наиболее поздние t^п сроки свершения событий. Любое событие не может наступить прежде, чем свершаться все предшествующие ему события и не будут выполнены все предшествующие работы. Поэтому ранний (или ожидаемый) срок tp(i) свершения i-ого события определяется продолжительностью максимального пути, предшествующего этому событию:

t^p(i) = max(t(L_ni))

где L_ni – любой путь, предшествующий i-ому событию, то есть путь от исходного до i-ого события сети.

Если событие j имеет несколько предшествующих путей, а следовательно, несколько предшествующих событий i, то ранний срок свершения события j удобно находить по формуле:

t^p(j) = max[t^p(i) + t(i,j)]

Задержка свершения события i по отношению к своему раннему сроку не отразится на сроке свершения завершающего события (а значит, и на сроке выполнения комплекса работ) до тех пор, пока сумма срока свершения этого события и продолжительности (длины) максимального из следующих за ним путей не превысит длины критического пути. Поэтому поздний (или предельный) срок t^п(i) свершения i-ого события равен:

t^п(i) = t_kp - max(t(L_ci))

где L_ci - любой путь, следующий за i-ым событием, т.е. путь от i-ого до завершающего события сети.

Если событие i имеет несколько последующих путей, а следовательно, несколько последующих событий j, то поздний срок свершения события i удобно находить по формуле:

t^п(i) = min[t^п(j) - t(i,j)]

Резерв времени R(i) i-ого события определяется как разность между поздним и ранним сроками его свершения:

R(i) = t^п(i) - t^p(i)

Резерв времени события показывает, на какой допустимый период времени можно задержать наступление этого события, не вызывая при этом увеличения срока выполнения комплекса работ.

Критические события резервов времени не имеют, так как любая задержка в свершении события, лежащего на критическом пути, вызовет такую же задержку в свершении завершающего события. Таким образом, определив ранний срок наступления завершающего события сети, мы тем самым определяем длину критического пути.

При определении ранних сроков свершения событий tp(i) двигаемся по сетевому графику слева направо и используем формулы (1), (2).

Расчет сроков свершения событий.

Для i=1 (начального события), очевидно tp(1)=0.

i=2: t^p(2) = t^p(1) + t(1,2) = 0 + 10 = 10.

i=3: max(t^p(1) + t(1,3);t^p(2) + t(2,3)) = max(0 + 5;10 + 3) = 13.

i=4: max(t^p(1) + t(1,4);t^p(3) + t(3,4)) = max(0 + 8;13 + 7) = 20.

i=5: t^p(5) = t^p(2) + t(2,5) = 10 + 11 = 21.

i=6: max(t^p(2) + t(2,6);t^p(3) + t(3,6);t^p(4) + t(4,6);t^p(5) + t(5,6)) = max(10 + 15;13 + 6;20 + 11;21 + 12) = 33.

i=7: t^p(7) = t^p(6) + t(6,7) = 33 + 10 = 43.

i=8: max(t^p(6) + t(6,8);t^p(7) + t(7,8)) = max(33 + 6;43 + 8) = 51.

i=9: max(t^p(5) + t(5,9);t^p(7) + t(7,9);t^p(8) + t(8,9)) = max(21 + 7;43 + 15;51 + 10) = 61.

Длина критического пути равна раннему сроку свершения завершающего события 9: t_kp=tp(9)=61

При определении поздних сроков свершения событий t_п(i) двигаемся по сети в обратном направлении, то есть справа налево и используем формулы (3), (4).

Для i=9 (завершающего события) поздний срок свершения события должен равняться его раннему сроку (иначе изменится длина критического пути): t^п(9)= t^р(9)=61

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 8. Просматриваются все строчки, начинающиеся с номера 8.

i=8: t^п(8) = t^п(9) - t(8,9) = 61 - 10 = 51.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 7. Просматриваются все строчки, начинающиеся с номера 7.

i=7: min(t^п(8) - t(7,8);t^п(9) - t(7,9)) = min(51 - 8;61 - 15) = 43.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 6. Просматриваются все строчки, начинающиеся с номера 6.

i=6: min(t^п(7) - t(6,7);t^п(8) - t(6,8)) = min(43 - 10;51 - 6) = 33.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 4. Просматриваются все строчки, начинающиеся с номера 4.

i=4: t^п(4) = t^п(6) - t(4,6) = 33 - 11 = 22.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 5. Просматриваются все строчки, начинающиеся с номера 5.

i=5: min(t^п(6) - t(5,6);t^п(9) - t(5,9)) = min(33 - 12;61 - 7) = 21.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 3. Просматриваются все строчки, начинающиеся с номера 3.

i=3: min(t^п(4) - t(3,4);t^п(6) - t(3,6)) = min(22 - 7;33 - 6) = 15.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 2. Просматриваются все строчки, начинающиеся с номера 2.

i=2: min(t^п(3) - t(2,3);t^п(5) - t(2,5);t^п(6) - t(2,6)) = min(15 - 3;21 - 11;33 - 15) = 10.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 1. Просматриваются все строчки, начинающиеся с номера 1.

i=1: min(t^п(2) - t(1,2);t^п(3) - t(1,3);t^п(4) - t(1,4)) = min(10 - 10;15 - 5;22 - 8) = 0.

Таблица 1 - Расчет резерва событий

Номер события	Сроки свершения события: ранний tp(i)	Сроки свершения события: поздний tп(i)	Резерв времени, R(i)
1		0	0
2	10	10	0
3	13	15	2
4	20	22	2
5	21	21	0
6	33	33	0
7	43	43	0
8	51	51	0
9	61	61	0

Заполнение таблицы 2.

Перечень работ и их продолжительность перенесем во вторую и третью графы. При этом работы следует записывать в графу 2 последовательно: сначала начиная с номера 1, затем с номера 2 и т.д.

Во второй графе поставим число, характеризующее количество непосредственно предшествующих работ (КПР) тому событию, с которого начинается рассматриваемая работа.

Так, для работы (3,4) в графу 1 поставим число 2, т.к. на номер 3 оканчиваются 2 работы: (1,3),(2,3).

Графу 4 получаем из таблицы 1 (t^p(i)). Графу 7 получаем из таблицы 1 (t^п(i)).

Значения в графе 5 получаются в результате суммирования граф 3 и 4.

В графе 6 позднее начало работы определяется как разность позднего окончания этих работ и их продолжительности (из значений графы 7 вычитаются данные графы 3);

Содержимое графы 8 (полный резерв времени R(ij)) равно разности граф 6 и 4 или граф 7 и 5. Если R(ij) равен нулю, то работа является критической

Полный резерв пути показывает, на сколько в сумме может быть увеличена продолжительность всех работ, принадлежащих данному пути, при условии, что срок выполнения всего комплекса работ не изменится. Образовывается, когда предшествующие работы закончатся в свой наиболее ранний срок.

Находим полный резерв R^П_i-j = Tп_j-t_i-j-Tр_i

R^П_(1,2) = 10-10-0 = 0

R^П_(1,3) = 15-5-0 = 10

R^П_(1,4) = 22-8-0 = 14

R^П_(2,3) = 15-3-10 = 2

R^П_(2,5) = 21-11-10 = 0

R^П_(2,6) = 33-15-10 = 8

R^П_(3,4) = 22-7-13 = 2

R^П_(3,6) = 33-6-13 = 14

R^П_(4,6) = 33-11-20 = 2

R^П_(5,6) = 33-12-21 = 0

R^П_(5,9) = 61-7-21 = 33

R^П_(6,7) = 43-10-33 = 0

R^П_(6,8) = 51-6-33 = 12

R^П_(7,8) = 51-8-43 = 0

R^П_(7,9) = 61-15-43 = 3

R^П_(8,9) = 61-10-51 = 0

Свободный резерв времени также можно найти и по формуле R^C_i-j = Tп_i-t_i-j-Tр_i

R^C_(1,2) = 10-10-0 = 0

R^C_(1,3) = 13-5-0 = 8

R^C_(1,4) = 20-8-0 = 12

R^C_(2,3) = 13-3-10 = 0

R^C_(2,5) = 21-11-10 = 0

R^C_(2,6) = 33-15-10 = 8

R^C_(3,4) = 20-7-13 = 0

R^C_(3,6) = 33-6-13 = 14

R^C_(4,6) = 33-11-20 = 2

R^C_(5,6) = 33-12-21 = 0

R^C_(5,9) = 61-7-21 = 33

R^C_(6,7) = 43-10-33 = 0

R^C_(6,8) = 51-6-33 = 12

R^C_(7,8) = 51-8-43 = 0

R^C_(7,9) = 61-15-43 = 3

R^C_(8,9) = 61-10-51 = 0

Независимый резерв времени также можно найти и по формуле R^Н_i-j = Tр_j-t_i-j-Tп_i

R^Н_(1,2) = 10-10-0 = 0

R^Н_(1,3) = 13-5-0 = 8

R^Н_(1,4) = 20-8-0 = 12

R^Н_(2,3) = 13-3-10 = 0

R^Н_(2,5) = 21-11-10 = 0

R^Н_(2,6) = 33-15-10 = 8

R^Н_(3,4) = 20-7-15 = -2

R^Н_(3,6) = 33-6-15 = 12

R^Н_(4,6) = 33-11-22 = 0

R^Н_(5,6) = 33-12-21 = 0

R^Н_(5,9) = 61-7-21 = 33

R^Н_(6,7) = 43-10-33 = 0

R^Н_(6,8) = 51-6-33 = 12

R^Н_(7,8) = 51-8-43 = 0

R^Н_(7,9) = 61-15-43 = 3

R^Н_(8,9) = 61-10-51 = 0

Таблица 2 - Анализ сетевой модели по времени

Работа (i,j)	Количество предшествующих работ	Продолжительность tij	Ранние сроки: начало tijР.Н.	Ранние сроки: окончание tijР.О.	Поздние сроки: начало tijП.Н.	Поздние сроки: окончание tijП.О.	Резервы времени: полный RijП	Независимый резерв времени RijН	Частный резерв I рода, Rij1	Частный резерв II рода, RijC
(1,2)	0	10	0	10	0	10	0	0	0	0
(1,3)	0	5	0	5	10	15	10	8	10	8
(1,4)	0	8	0	8	14	22	14	12	14	12
(2,3)	1	3	10	13	12	15	2	0	2	0
(2,5)	1	11	10	21	10	21	0	0	0	0
(2,6)	1	15	10	25	18	33	8	8	8	8
(3,4)	2	7	13	20	15	22	2	-2	0	0
(3,6)	2	6	13	19	27	33	14	12	12	14
(4,6)	2	11	20	31	22	33	2	0	0	2
(5,6)	1	12	21	33	21	33	0	0	0	0
(5,9)	1	7	21	28	54	61	33	33	33	33
(6,7)	4	10	33	43	33	43	0	0	0	0
(6,8)	4	6	33	39	45	51	12	12	12	12
(7,8)	1	8	43	51	43	51	0	0	0	0
(7,9)	1	15	43	58	46	61	3	3	3	3
(8,9)	2	10	51	61	51	61	0	0	0	0

Следует отметить, что кроме полного резерва времени работы, выделяют еще три разновидности резервов. Частный резерв времени первого вида R₁ - часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом позднего срока ее начального события. R₁ находится по формуле:

R(i,j)= R^п(i,j) - R(i)

Частный резерв времени второго вида, или свободный резерв времени Rc работы (i,j) представляет собой часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом раннего срока ее конечного события. Rc находится по формуле:

R(i,j)= R^п(i,j) - R(j)

Значение свободного резерва времени работы указывает на расположение резервов, необходимых для оптимизации.

Независимый резерв времени Rн работы (i,j) - часть полного резерва, получаемая для случая, когда все предшествующие работы заканчиваются в поздние сроки, а все последующие начинаются в ранние сроки. Rн находится по формуле:

R(i,j)= R^п(i,j)- R(i) - R(j)

Критический путь: (1,2)(2,5)(5,6)(6,7)(7,8)(8,9)

Продолжительность критического пути: 61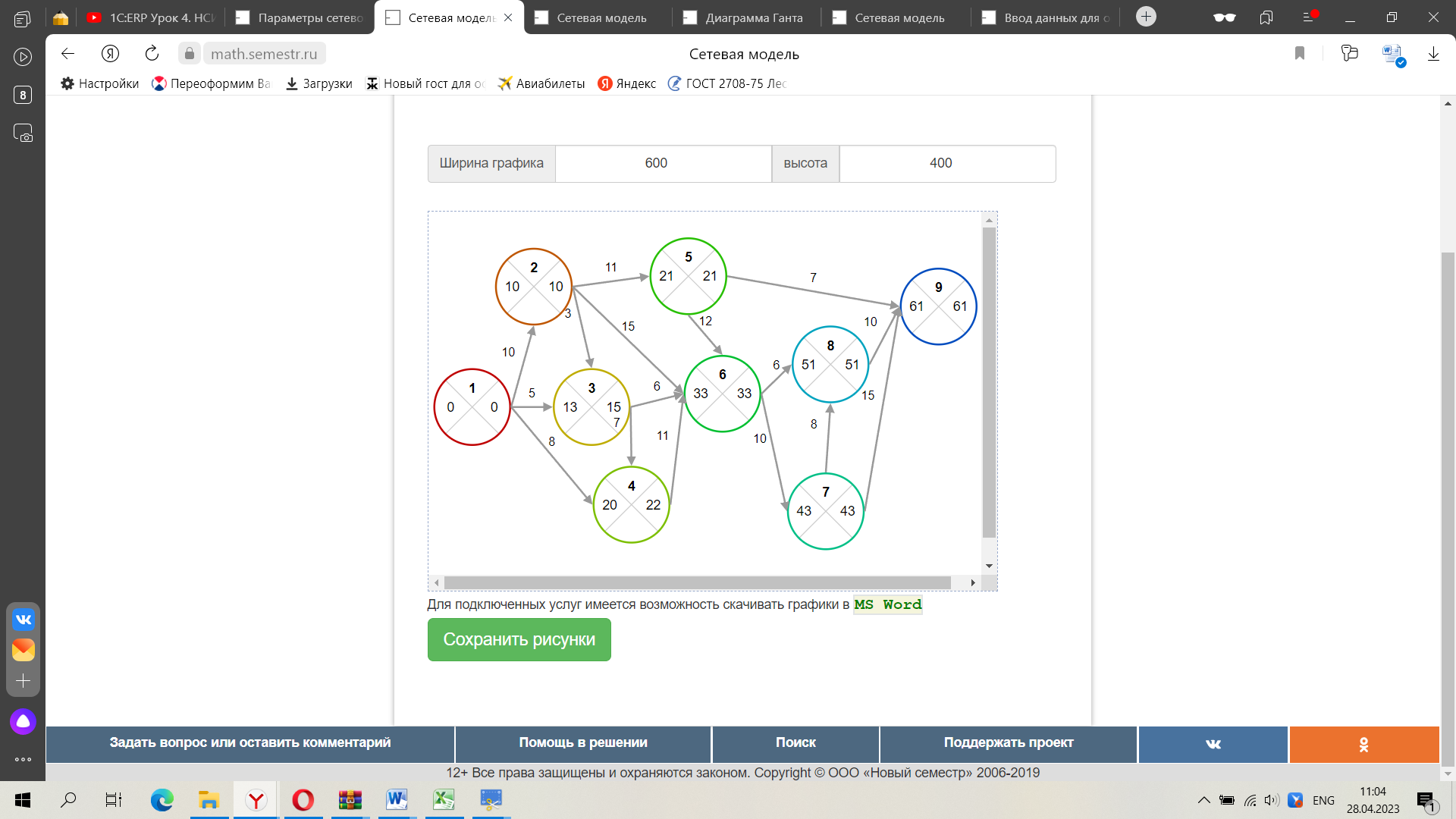



Рис. Сетевой график

Сложность сетевого графика оценивается коэффициентом сложности, который определяется по формуле:

K_c = n_pab / n_cob

где K_c – коэффициент сложности сетевого графика; n_pab – количество работ, ед.; n_cob – количество событий, ед.

Сетевые графики, имеющие коэффициент сложности от 1,0 до 1,5, являются простыми, от 1,51 до 2,0 – средней сложности, более 2,1 – сложными.

K_c = 16 / 9 = 1.78

Поскольку 1.51 < Kc < 2, то сетевой график является средней сложности.

Коэффициентом напряженности К_H работы P_i,j называется отношение продолжительности несовпадающих (заключенных между одними и теми же событиями) отрезков пути, одним из которых является путь максимальной продолжительности, проходящий через данную работу, а другим – критический путь:

где t(Lmax) – продолжительность максимального пути, проходящего через работу P_i,j, от начала до конца сетевого графика; t_kp – продолжительность (длина) критического пути; t1_kp – продолжительность отрезка рассматриваемого максимального пути, совпадающего с критическим путем.

Коэффициент напряженности К_H работы P_i,j может изменяться в пределах от 0 (для работ, у которых отрезки максимального из путей, не совпадающие с критическим путем, состоят из фиктивных работ нулевой продолжительности) до 1 (для работ критического пути). Чем ближе к 1 коэффициент напряженности К_H работы P_i,j, тем сложнее выполнить данную работу в установленные сроки. Чем ближе Кн работы P_i,j к нулю, тем большим относительным резервом обладает максимальный путь, проходящий через данную работу.

Работа	Путь	Максимальный путь, t(Lmax)	Совпадающие работы	t1kp	Расчет	КH
(1,2)	(1,2)(2,5)(5,6)(6,7)(7,8)(8,9)	61	(1,2)(2,5)(5,6)(6,7)(7,8)(8,9)	61	-	-
(1,3)	(1,3)(3,4)(4,6)(6,7)(7,8)(8,9)	51	(6,7)(7,8)(8,9)	28	(51-28)/(61-28)	0.697
(1,4)	(1,4)(4,6)(6,7)(7,8)(8,9)	47	(6,7)(7,8)(8,9)	28	(47-28)/(61-28)	0.576
(2,3)	(1,2)(2,3)(3,4)(4,6)(6,7)(7,8)(8,9)	59	(1,2)(6,7)(7,8)(8,9)	38	(59-38)/(61-38)	0.913
(2,5)	(1,2)(2,5)(5,6)(6,7)(7,8)(8,9)	61	(1,2)(2,5)(5,6)(6,7)(7,8)(8,9)	61	-	-
(2,6)	(1,2)(2,6)(6,7)(7,8)(8,9)	53	(1,2)(6,7)(7,8)(8,9)	38	(53-38)/(61-38)	0.652
(3,4)	(1,2)(2,3)(3,4)(4,6)(6,7)(7,8)(8,9)	59	(1,2)(6,7)(7,8)(8,9)	38	(59-38)/(61-38)	0.913
(3,6)	(1,2)(2,3)(3,6)(6,7)(7,8)(8,9)	47	(1,2)(6,7)(7,8)(8,9)	38	(47-38)/(61-38)	0.391
(4,6)	(1,2)(2,3)(3,4)(4,6)(6,7)(7,8)(8,9)	59	(1,2)(6,7)(7,8)(8,9)	38	(59-38)/(61-38)	0.913
(5,6)	(1,2)(2,5)(5,6)(6,7)(7,8)(8,9)	61	(1,2)(2,5)(5,6)(6,7)(7,8)(8,9)	61	-	-
(5,9)	(1,2)(2,5)(5,9)	28	(1,2)(2,5)	21	(28-21)/(61-21)	0.175
(6,7)	(1,2)(2,5)(5,6)(6,7)(7,8)(8,9)	61	(1,2)(2,5)(5,6)(6,7)(7,8)(8,9)	61	-	-
(6,8)	(1,2)(2,5)(5,6)(6,8)(8,9)	49	(1,2)(2,5)(5,6)(8,9)	43	(49-43)/(61-43)	0.333
(7,8)	(1,2)(2,5)(5,6)(6,7)(7,8)(8,9)	61	(1,2)(2,5)(5,6)(6,7)(7,8)(8,9)	61	-	-
(7,9)	(1,2)(2,5)(5,6)(6,7)(7,9)	58	(1,2)(2,5)(5,6)(6,7)	43	(58-43)/(61-43)	0.833
(8,9)	(1,2)(2,5)(5,6)(6,7)(7,8)(8,9)	61	(1,2)(2,5)(5,6)(6,7)(7,8)(8,9)	61	-	-

Вычисленные коэффициенты напряженности позволяют дополнительно классифицировать работы по зонам. В зависимости от величины Кн выделяют три зоны: критическую (Кн > 0,8); подкритическую (0,6 < Кн < 0,8); резервную (Кн < 0,6).

Сократим критический путь на 1 день за минимальную доплату к ранее найденной стоимости в нормальном режиме выполнения работ.

Прежде всего, установим, за какую минимальную доплату можно завершить комплекс работ за 60 дня вместо 61 дней. Сокращение срока на день возможно только за счет уменьшения на один день продолжительности критического пути. Это, в свою очередь, можно достичь, ускоряя на день какие-либо критические работы, лежащие на этих путях. Для того, чтобы установить какие критические работы в совокупности ускорять дешевле, нужно вычислить средние стоимости 1 дня ускорения всех выявленных критических работ.

Рассмотрим критическую работу (1,2), ее можно ускорить с 10 до 0 дней, доплатив за это 0 д.е. Отсюда среднюю стоимость дня ускорения работы найдем по формуле:

Рассмотрим критическую работу (2,5), ее можно ускорить с 11 до 0 дней, доплатив за это 0 д.е.

Рассмотрим критическую работу (5,6), ее можно ускорить с 12 до 0 дней, доплатив за это 0 д.е.

Рассмотрим критическую работу (6,7), ее можно ускорить с 10 до 0 дней, доплатив за это 0 д.е.

Рассмотрим критическую работу (7,8), ее можно ускорить с 8 до 0 дней, доплатив за это 0 д.е.

Рассмотрим критическую работу (8,9), ее можно ускорить с 10 до 0 дней, доплатив за это 0 д.е.

После проведенных расчетов, очевидно, что уменьшение продолжительности критического пути (1,2)(2,5)(5,6)(6,7)(7,8)(8,9) на один день следует проводить за счет ускорения работы (1,2) с доплатой 0 д.е.

В итоге самым дешевым вариантом для сокращения срока на 1 день является ускорение на один день работ [(1,2)], что приведет к новому критическому сроку 60 дня с минимальной доплатой 0 = 0 д.е.

Выполним запланированные ускорения работ [(1,2)] и сделаем перерасчет временных характеристик сетевого графика.

Отсюда итоговая стоимость составит 0 + 0 = 0 д.е.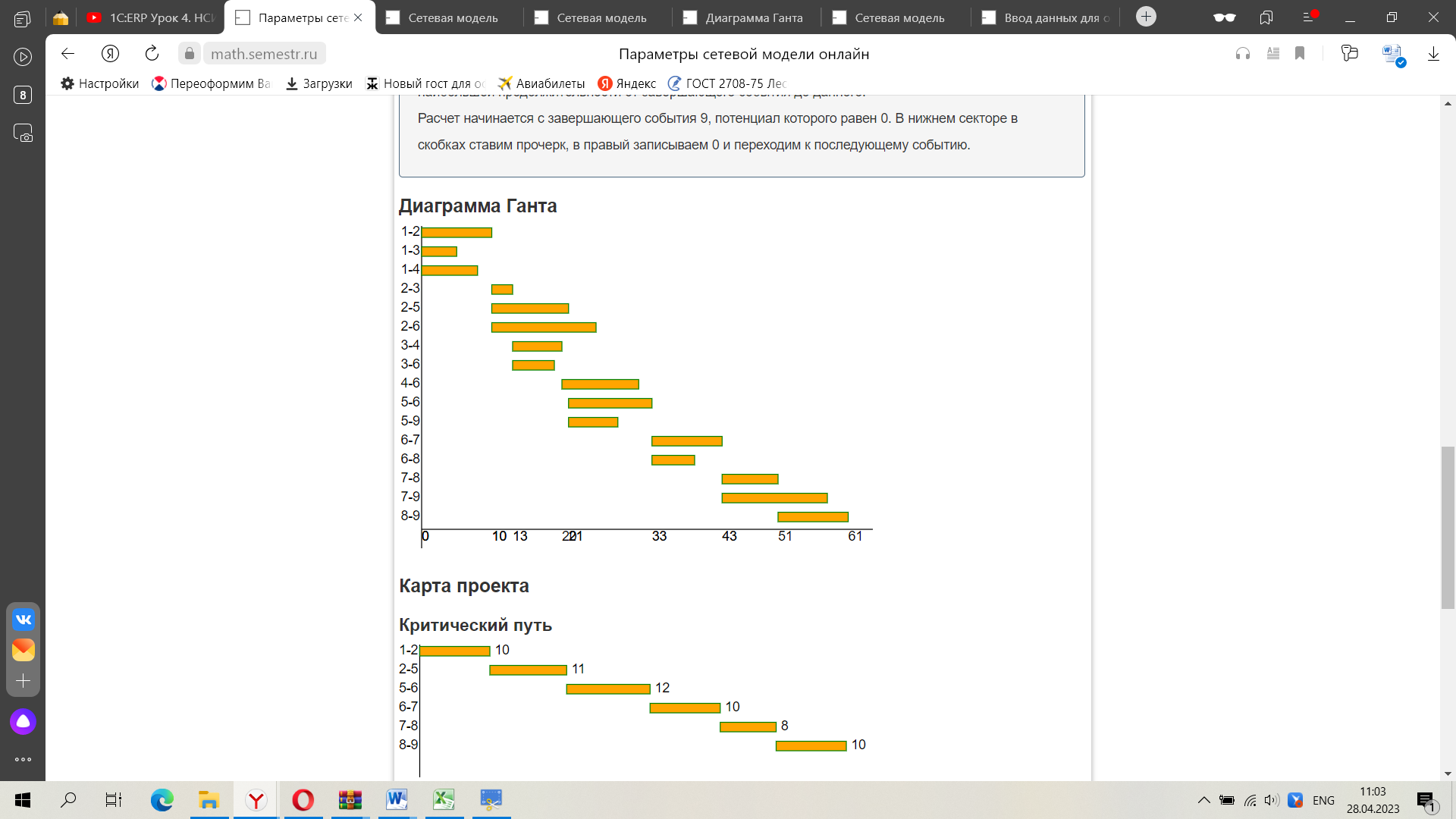



Рис. Диаграмма Ганта