Алина№2. Сформулируем поставленную задачу математически в виде соответствующей задачи лп
 Скачать 28.64 Kb. Скачать 28.64 Kb.
|
|
Сформулируем поставленную задачу математически в виде соответствующей задачи ЛП: Найти наибольшее значение функции F = 40x1 + 50x2 при следующих ограничениях: 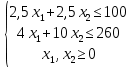 Рассмотрим неравенство 1 системы ограничений. 2,5x1 + 2,5x2 ≤ 100 Построим прямую: 2,5x1 + 2,5x2 = 100 Пусть x1 =0 => 2,5x2 = 100 => x2 = 40 Пусть x2 =0 => 2,5x1 = 100 => x1 = 40 Найдены координаты двух точек (0, 40) и (40 ,0). Соединяем их и получаем необходимую прямую (1). Рассмотрим неравенство 2 системы ограничений. 4 x1 + 10 x2 ≤ 260 Построим прямую: 4 x1 + 10 x2 = 260 Пусть x1 =0 => 10 x2 = 260 => x2 = 26 Пусть x2 =0 => 4 x1 = 260 => x1 = 65 Найдены координаты двух точек (0, 26) и (65 ,0). Соединяем их и получаем необходимую прямую (2). Строим область допустимых решений: 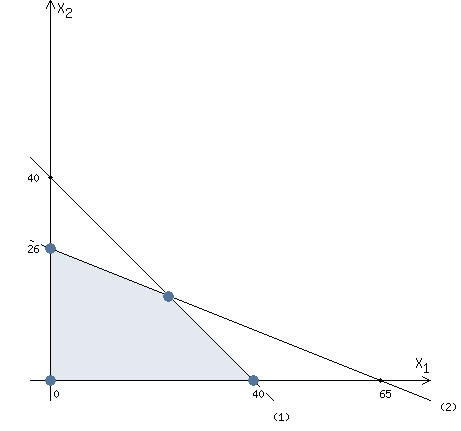 Строим вектор C = (40, 50), координатами которого являются коэффициенты функции F. Функция F достигает наибольшего значения в точке A. 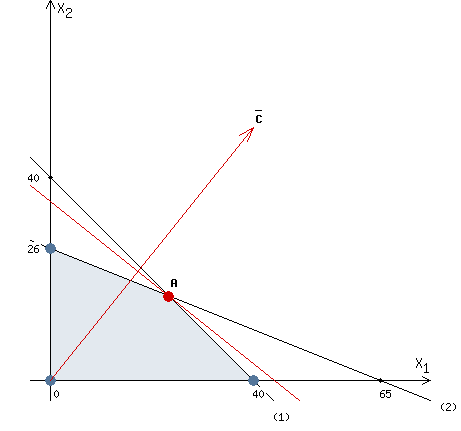 Точка A одновременно принадлежит прямым (1) и (2). 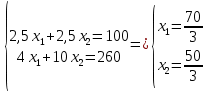 Вычислим значение функции F в точке A (70/3,50/3). F (A) = 40 * 70/3 + 50 * 50/3 = 5300/3. Приведем задачу к каноническому виду. Вводим в 1м неравенстве базисную переменную x3. Во 2м неравенстве базисную переменную x4. Получаем: 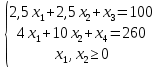 Построим двойственную задачу к исходной. Количество переменных в двойственной задаче равно количеству неравенств в исходной. Матрица коэффициентов двойственной задачи является транспонированной к матрице коэффициентов исходной. Система ограничений двойственной задачи записывается в виде неравенств противоположного смысла неравенствам системы ограничений прямой задачи. Получаем: 100y1+260y2 → min 2.5y1+4y2≥40 2.5y1+10y2≥50 y1,y2 ≥ 0 Решим данную задачу графически. Рассмотрим неравенство 1 системы ограничений. 2,5x1 + 4x2 ≥ 40 Построим прямую: 2,5x1 + 4x2 = 40 Пусть x1 =0 => 4 x2 = 40 => x2 = 10 Пусть x2 =0 => 2,5x1 = 40 => x1 = 16 Найдены координаты двух точек (0, 10) и (16 ,0). Соединяем их и получаем необходимую прямую (1). Рассмотрим неравенство 2 системы ограничений. 25/10 x1 + 10 x2 ≥ 50 Построим прямую: 25/10 x1 + 10 x2 = 50 Пусть x1 =0 => 10 x2 = 50 => x2 = 5 Пусть x2 =0 => 25/10 x1 = 50 => x1 = 20 Найдены координаты двух точек (0, 5) и (20 ,0). Соединяем их и получаем необходимую прямую (2). Строим область допустимых решений: 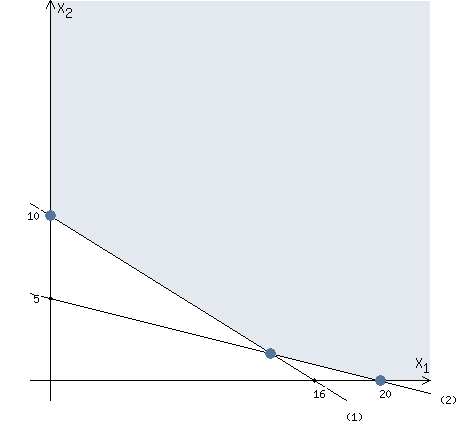 Строим вектор C = (100, 260), координатами которого являются коэффициенты функции F. Функция F достигает наименьшего значения в точке A. 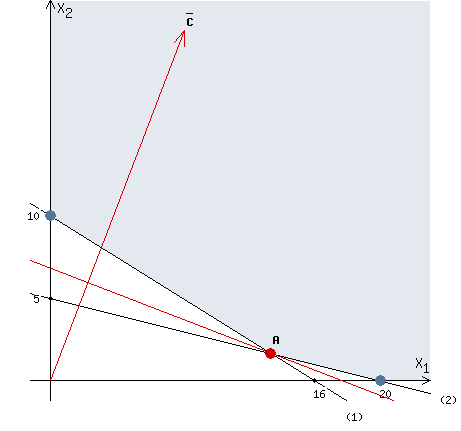 Точка A одновременно принадлежит прямым (1) и (2). 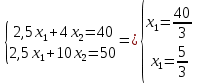 Вычислим значение функции F в точке A (40/3,5/3). F (A) = 100 * 40/3 + 260 * 5/3 = 5300/3. Проверка оптимальности: Решение прямой и двойственной задач совпадают ! |
