Бернулли. Схема Бернулли
 Скачать 42.27 Kb.
|
|
Тема: «Схема Бернулли» Теорема Бернулли (n≤10, p>0.1) Теорема: Пусть производится n-независимых испытаний. Вероятность того, что в n-независимых испытаниях, в каждом из которых вероятность одинакова и равна p(n≤10, p>0.1), событие появиться ровно k-раз, вычисляется по формуле: 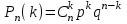 ( )Локальная теорема Лапласа (n>10, p>0.1) Теорема: Вероятность того, что в n-независимых испытаниях, в каждом из которых вероятность одинакова и равна p(n>10, p>0.1), событие появиться ровно k-раз, вычисляется по формуле:  ,  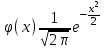,   (чётная). Если х 4, то  .Интегральная теорема Лапласа (от k1 до k2 раз) Теорема: Вероятность того, что в n-независимых испытаниях, в каждом из которых вероятность одинакова и равна p, событие появиться от k1 до k2 раз, вычисляется по формуле:  ,  , ,  , 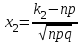 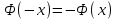(нечётная).Если х 4, то  .Теорема Пуассона (n>10, p≤0.1) Теорема: Вероятность того, что в n-независимых испытаниях, в каждом из которых вероятность одинакова и равна p(n>10, p≤0.1), событие появиться ровно k-раз, вычисляется по формул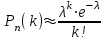е:  где  Оценка отклонения Теорема: Вероятность того, что в n-независимых испытаниях, в каждом из которых вероятность одинакова и равна p, относительная частота события отклоняется от его вероятности на величину 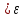 , приближенно равна удвоенной интегральной функции Лапласа: , где  .Наивероятнейшее число Теорема: Число k0 наступления события A в n-независимых испытаниях, в каждом из которых вероятность одинакова и равна p, называют наивероятнейшем, если вероятность события А наступит в этих испытанияхk-раз превышает вероятности остальных возможных исходов:  |