Локальная и интегральная формулы Муавра лапласа. Тема 3(Локальная и интегральная формулы Муавра-Лапласа). Решение По условию, n 400 k 80 р 0,2 q 0 Воспользуемся асимптотической формулой Лапласа
 Скачать 21.78 Kb. Скачать 21.78 Kb.
|
|
Локальная и интегральная формулы Муавра-Лапласа 1.Найти приближенно вероятность того, что при 400 испытаниях событие наступит ровно 104 раза, если вероятность его появления в каждом испытании равна 0,2. Решение: По условию, n = 400; k = 80; р = 0,2; q = 0,8. Воспользуемся асимптотической формулой Лапласа: 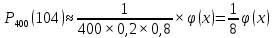 Вычислим определяемое данными задачи значение х: 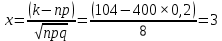 По таблице находим 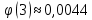 Искомая вероятность: 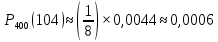 Ответ: 0,0006 2.Вероятность изготовления детали высшего сорта на данном станке равна 0,4. Найти вероятность того, что среди наудачу взятых 26 деталей половина окажется высшего сорта. Решение: По условию, n = 26; k = 13; р = 0,4; q = 0,6. np=26*0,4= 10,4; 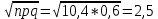 ; k-np=2,6. ; k-np=2,6.Вычислим определяемое данными задачи значение х: 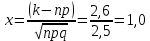 4 4По таблице находим 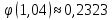 Воспользуемся локальной теоремой Лапласа: 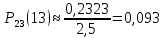 Ответ: 0,093 3.Сколько раз с вероятностью 0,0484 можно ожидать появление события А в 100 независимых испытаниях, если вероятность его появления в отдельном испытании равна 0,5. Решение: По условию, n = 100; Рn(k) = 13; р = 0,5; q = 0,5. Вычислим определяемое данными задачи значение х: 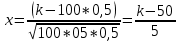 , , тогда 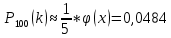 Отсюда находим 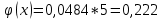 По таблице находим 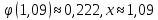 Подставляем значения: 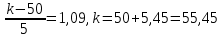 Поскольку k – целое число, то k=55 Ответ: 55 4.Вероятность изготовления стандартной детали равна 0,98. Какова вероятность того, что среди 50 деталей окажется одна нестандартная? (задачу решить по теореме Лапласа, формуле Пуассона и по формуле Бернулли). Решение: 𝑛 = 50; 𝑝 = 1 − 0,98 = 0,02; 𝑞 = 0,98; 𝑚 = 1 𝑛𝑝 = 50 * 0,02 = 1; 𝑛𝑝𝑞 = 50 * 0,02 * 0,98 = 0,98 Значения функции 𝜑(𝑥) являются табличными; 𝜑 (0) = 0,3989, тогда: Применим локальную теорему Муавра-Лапласа: 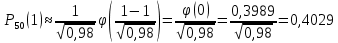 Применим формулу Пуассона: 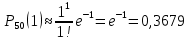 Применим формулу Бернулли: 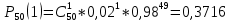 Самая точная формула - Бернулли, остальные приближенные. Ответ: по теореме Лапласа – 0,4029, по формуле Пуассона – 0,3679, по формуле Бернулли – 0,3716. 5.При установившемся технологическом процессе фабрика выпускает в среднем 70 % продукции 1-го сорта. Чему равна вероятность того, что в партии из 1000 изделий число первосортных заключено между 652 и 760? Решение: По условию, n = 1000; р = 0,7; q = 0,3, a = 652, b = 760 Искомую вероятность находим по формуле: 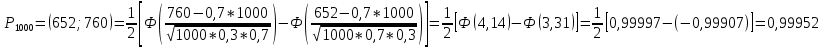 Ответ: 0,99952 6.Вероятность появления события в каждом из 100 независимых испытаний постоянна и равна р = 0,8. Найти вероятность того, что событие появится: 1) не менее 75 и не более 90 раз; 2) не менее 75 раз; 3) не более 74 раз. Решение: по условию, n=100; p=0,8; q=0,2; k1=75; k2=90 1) Вычислим определяемое данными задачи значение для х1: 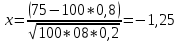 Вычислим определяемое данными задачи значение для х2: 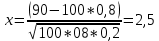 Учитывая, что функция Лапласа нечетна, т.е. Ф(-x) =-Ф(x), получим 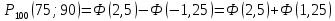 По таблице значений функции найдем: Ф (2,5) =0,4938; Ф (1,25) =0,3944. Искомая вероятность: Р100(75;90) =0,4938+0,3944=0,8882. 2) Требование, чтобы событие появилось не менее 75 раз, означает, что число появлений события может быть равно 75 либо 76, …, либо 100. Таким образом, в рассматриваемом случае следует принять k1=75, k2=100. Тогда Вычислим определяемое данными задачи значение для х1:  Вычислим определяемое данными задачи значение для х2:  По таблице найдем Ф (1,25) =0,3944; Ф (5) =0,5. Искомая вероятность Р100(75;100) =Ф (5)-Ф (-1,25) =Ф (5) +Ф (1,25) =0,5+0,3944=0,8944. 3) События – “А появилось не менее 75 раз” и “А появилось не более 74 раз” противоположны, поэтому сумма вероятностей этих событий равна единице. Следовательно, искомая вероятность Р100(0;74) =1- Р100(75;100) =1-0,8944=0,1056. Ответ: 1) 0,8882; 2) 0,8944; 3) 0,1056. 7.Найти вероятность того, что в партии из 400 изделий отклонение числа изделий первого сорта от наивероятнейшего числа не превысит по абсолютной величине 25, если вероятность появления изделия первого сорта равна 0,7. Решение: 𝑛 = 400; 𝑝 = 0,7; 𝑛𝑝 = 400 * 0,7 = 280 Наивероятнейшее число изделий первого сорта: 𝑛𝑝 = 280 Вероятность того, что в партии из 400 изделий отклонение числа изделий первого сорта от наивероятнейшего числа не превысит по абсолютной величине 25, найдем по формуле (следствие из интегральной теоремы Муавра-Лапласа): s = 25; 𝑞 = 1 − 𝑝 = 0,3; 𝑛𝑝𝑞 = 400 * 0,7 * 0,3 = 84  Ответ: 0,9936. 8.Вероятность появления события в каждом из 625независимых испытаний равна 0,8. Найти вероятность того, что относительная частота появления события отклонится от его вероятности по абсолютной величине не более, чем на 0,04 Решение: по условию, n=625; p=0,8; q=0,2; =0,04 Требуется найти вероятность  . . Воспользуемся формулой: 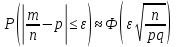 , тогда , тогда 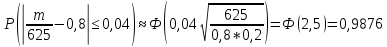 Ответ: 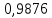 |
