|
|
Специфика изменений КИМ ЕГЭ и критериев оценивания по математике. Щербакова Н.А. Новосергиевский район МАТЕМАТИКА. Щербакова Наталья Алексеевна, учитель математики мобу Нестеровская сош
Задание и пример его выполнения
  12. а) Решите уравнение 2sin (𝑥 + 3) + cos 2𝑥 = √3cos 𝑥 + 1 12. а) Решите уравнение 2sin (𝑥 + 3) + cos 2𝑥 = √3cos 𝑥 + 1
 б) Укажите корни этого уравнения, принадлежащие отрезку [−3𝜋; −3𝜋] б) Укажите корни этого уравнения, принадлежащие отрезку [−3𝜋; −3𝜋]
Решение. а) Запишем исходное уравнение в виде:
  sin 𝑥 + √3cos 𝑥 + 1 − 2sin2 𝑥 =√3 cos 𝑥 + 1; sin 𝑥 − 2sin2 𝑥 = 0 sin 𝑥 + √3cos 𝑥 + 1 − 2sin2 𝑥 =√3 cos 𝑥 + 1; sin 𝑥 − 2sin2 𝑥 = 0
sin 𝑥 ∙ (2sin 𝑥 − 1)=0
 Значит sin 𝑥 = 0, откуда x=𝜋𝑘, k ∈ , или sin 𝑥=1 откуда x=𝜋+2𝜋𝑛, n∈ или Значит sin 𝑥 = 0, откуда x=𝜋𝑘, k ∈ , или sin 𝑥=1 откуда x=𝜋+2𝜋𝑛, n∈ или
 x=5𝜋+2𝜋𝑚, m∈ x=5𝜋+2𝜋𝑚, m∈
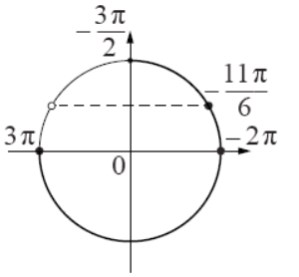  Б) с помощью числовой окружности отберем корни принадлежащие отрезку [−3𝜋; −3𝜋]. Б) с помощью числовой окружности отберем корни принадлежащие отрезку [−3𝜋; −3𝜋].
 Получим числа: -3𝜋; 2 𝜋; -11𝜋 Получим числа: -3𝜋; 2 𝜋; -11𝜋
  Ответ: a) 𝜋𝑘, k ∈ ; 𝜋+2𝜋𝑛, n∈ ;5𝜋+2𝜋𝑚, m∈ б) -3𝜋; 2 𝜋; -11𝜋 Ответ: a) 𝜋𝑘, k ∈ ; 𝜋+2𝜋𝑛, n∈ ;5𝜋+2𝜋𝑚, m∈ б) -3𝜋; 2 𝜋; -11𝜋
1 балл
Комментарий: а) уравнение решено верно (без подробностей преобразования, видимо, сильный ученик не счёл нужным их писать)
б) отбор корней произведён верно, но есть недочёты в рисунке (не обозначен отрицательный корень -3𝜋)

ЗАДАНИЕ № 3. Заполните матрицу проектного замысла «Сложные задания ЕГЭ по математике», содержащую необходимую и достаточную информацию о проектном замысле.
Матрица проектного замысла состоит из: краткого описания проблемы;
разделов и тем, определяемых как «сложные»;
описания проектной идеи: что, как и с помощью каких механизмов, способов и средств будет изменено;
ресурсной карты проектного замысла: какие задания убрать из КИМ, варианты альтернативных заданий (не менее 2х).
Матрица проектного замысла
«Сложные задания ЕГЭ по математике»
Краткое описание проблемы
|
Разделы и темы, определяемые как «сложные»
|
Описание проектной идеи (что, как и с помощью каких механизмов, способов и средств будет изменено)
|
Ресурсная карта проектного замысла
|
№ 18. Решить уравнение или неравенство с параметрами, систему уравнений или неравенств с параметрами.
Эти задачи сложно классифицировать и дать общий алгоритм решения, поскольку каждая из них является нестандартной, но можно изучить основные приемы и методы. Не забывайте про особенности функций: монотонность, непрерывность, четность/нечетность, ограниченность, инвариантность и т. д. Для того чтобы осилить задачу с параметром, необходимо произвести несложные, но последовательные рассуждения и составить логическую схему решения.
|
2 часть ЕГЭ- задание № 18 с параметрами
|
Для начала попробуйте решить простое уравнение или неравенство с параметром из школьного учебника (линейное, квадратное, дробно-рациональное, тригонометрическое и т. п.). Сравните с решением аналогичного уравнения или неравенства без параметра. Следите за тем, как неопределенность значения коэффициента влияет на ход решения.
После того, как вы освоились с решением простейших задач с параметром, можете приступать к решению задач из открытых банков заданий. Выбирайте сначала задачи, допускающие решение аналитическим методом.
Особенность задач с параметрами заключается в возможности привлечь к их решению различные идеи и методы: решение в координатах, использование свойств элементарных функций
|
Задача 1.
Найти все значения параметра a, при каждом из которых уравнение

имеет единственное решение.
Задача 2
Найти все значения параметра а, при которых неравенство 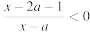 выполняется для всех х, таких, что выполняется для всех х, таких, что 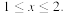
Задача 3
Найдите все значения a, при каждом из которых система 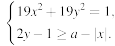
имеет ровно 2 решения.
|
№ 19. Решить задачу на числа и их свойства.
Представляет собой задачу на числа, для решения которой вполне достаточно знаний математики в объеме общеобразовательной программы. Главная ее сложность состоит в необходимости обнаружить скрытые закономерности на основе экспериментов с числами, придумать идею решения, а затем построить и исследовать подходящую модель в отношении описанной в задаче ситуации.
|
2 часть ЕГЭ задание № 19
|
Это задание олимпиадного уровня, поэтому оно требует нестандартного мышления. Для подготовки к нему можно изучить признаки делимости чисел, а также формулы арифметической и геометрической прогрессий. Помогут также решение олимпиадных заданий похожего типа.
|
Задача 1
На бумажке записаны три положительных числа: x, y и 1. За один ход разрешается записать на бумажку сумму или разность каких‐нибудь двух уже записанных чисел или записать число, обратное к какому‐нибудь из уже записанных чисел. Можно ли за несколько ходов получить на бумажке
а) число x2?
б) число xy?
Задача 2
а) Дано шесть натуральных чисел. Все они различны и дают в сумме 22. Найти эти числа.
б) Докажите, что других таких чисел нет.
в) Тот же вопрос про 100 чисел, дающих в сумме 5051.
Задача 3
Произведение трёх натуральных чисел, образующих арифметическую прогрессию, является делителем некоторого числа вида n2 + 1, где 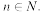
а) Существует ли такая арифметическая прогрессия с разностью 12.
б) Существует ли такая арифметическая прогрессия с разностью 10 или 11.
| |
|
|
 Скачать 53.97 Kb.
Скачать 53.97 Kb.
 12. а) Решите уравнение 2sin (𝑥 + 3) + cos 2𝑥 = √3cos 𝑥 + 1
12. а) Решите уравнение 2sin (𝑥 + 3) + cos 2𝑥 = √3cos 𝑥 + 1 б) Укажите корни этого уравнения, принадлежащие отрезку [−3𝜋; −3𝜋]
б) Укажите корни этого уравнения, принадлежащие отрезку [−3𝜋; −3𝜋]
 sin 𝑥 + √3cos 𝑥 + 1 − 2sin2 𝑥 =√3 cos 𝑥 + 1; sin 𝑥 − 2sin2 𝑥 = 0
sin 𝑥 + √3cos 𝑥 + 1 − 2sin2 𝑥 =√3 cos 𝑥 + 1; sin 𝑥 − 2sin2 𝑥 = 0 Значит sin 𝑥 = 0, откуда x=𝜋𝑘, k ∈ , или sin 𝑥=1 откуда x=𝜋+2𝜋𝑛, n∈ или
Значит sin 𝑥 = 0, откуда x=𝜋𝑘, k ∈ , или sin 𝑥=1 откуда x=𝜋+2𝜋𝑛, n∈ или x=5𝜋+2𝜋𝑚, m∈
x=5𝜋+2𝜋𝑚, m∈ 
 Б) с помощью числовой окружности отберем корни принадлежащие отрезку [−3𝜋; −3𝜋].
Б) с помощью числовой окружности отберем корни принадлежащие отрезку [−3𝜋; −3𝜋]. Получим числа: -3𝜋; 2 𝜋; -11𝜋
Получим числа: -3𝜋; 2 𝜋; -11𝜋
 Ответ: a) 𝜋𝑘, k ∈ ; 𝜋+2𝜋𝑛, n∈ ;5𝜋+2𝜋𝑚, m∈ б) -3𝜋; 2 𝜋; -11𝜋
Ответ: a) 𝜋𝑘, k ∈ ; 𝜋+2𝜋𝑛, n∈ ;5𝜋+2𝜋𝑚, m∈ б) -3𝜋; 2 𝜋; -11𝜋
