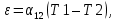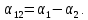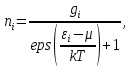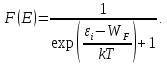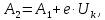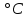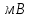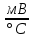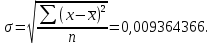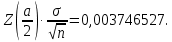Термопара_отчёт. Шикунова Дмитрия Алексеевича Выполнение Оформление сто 04. 012012 Устный отчет
 Скачать 1.05 Mb. Скачать 1.05 Mb.
|
|
МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «САРАТОВСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ Н.Г.ЧЕРНЫШЕВСКОГО» Кафедра материаловедения, технологии и управления качеством ТЕРМОПАРА ОТЧЁТ ПО ЛАБОРАТОРНОЙ РАБОТЕ по дисциплине «Материалы датчиков внешних воздействий» студента 4 курса 421 группы направления подготовки 22.03.01 «Материаловедение и технологии материалов», профиль «Материаловедение и технологии новых материалов», факультета нано- и биомедицинских технологий Шикунова Дмитрия Алексеевича
Саратов 2019 СОДЕРЖАНИЕВВЕДЕНИЕ 3 1 Теоретические основы 4 1.2 Эффект Зеебека и влияние температуры на распределение Ферми-Дирака в собственных и примесных полупроводниках 6 1.3 Влияние фононов и контактная разность потенциалов 8 1.4 Диффузионный ток 12 2 Практическая часть 14 ЗАКЛЮЧЕНИЕ 18 ВВЕДЕНИЕТермопара – пара проводников из различных материалов, соединённых на одном конце и формирующих часть устройства, использующего термоэлектрический эффект для измерения температуры. Существует несколько методов измерения температуры: оптические, механические и электрические методы. Измерение температуры термопарой основано на электрическом методе, основой которого является эффект Зеебека. Цель работы: найти чувствительность и определить материалы термопары. 1 Теоретические основы1.1 Принцип работы термопары Принцип работы термопары основан на эффекте Зеебека, который является одним из основных термоэлектрических явлений. Термоэлектрические явления – совокупность физических явлений, обусловленных взаимосвязью между тепловыми и электрическими процессами в металлах и полупроводниках. Эффект Зеебека состоит в том, что в замкнутой цепи, состоящей из разнородных проводников, возникает ЭДС, если места контактов поддерживают при разных температурах (термо-ЭДС.). В простейшем случае, когда электрическая цепь состоит из двух различных проводников, она называется термопарой. Величина термо-ЭДС зависит только от температур горячего T1 и холодного T2 контактов и от материала проводников. Когда концы проводника находятся при разных температурах, между ними возникает разность потенциалов, пропорциональная разности температур. Схема термопары представлена на рисунке 1. Термо-ЭДС материала чувствительна к микроскопическим количествам примесей, к ориентации кристаллических зёрен и обработке материала. По этой же причине термо-ЭДС может возникнуть в цепи, состоящей из одного и того же материала при наличии температурных перепадов, если разные участки цепи подвергались различным технологическим операциям. Однако ЭДС термопары не меняется при последовательном включении в цепь любого количества других материалов, если появляющиеся при этом дополнительные места контактов поддерживают при одной и той же температуре. Коэффициент пропорциональности называют коэффициентом термо-ЭДС. У разных металлов коэффициент термо-ЭДС разный и, соответственно, разность потенциалов, возникающая между концами разных проводников, будет различная. Помещая спай из металлов с отличными коэффициентами термо-ЭДС в среду с температурой Т1, мы получим напряжение между противоположными контактами, находящимися при другой температуре Т2, которое будет пропорционально разности температур Т1 и Т2 [1]. 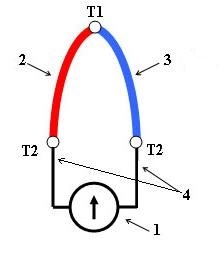 Рисунок 1 – Схема измерительного прибора, где 1 – измерительный прибор; 2, 3 – электроды; 4 – соединительные провода; T1 и Т2 – температура «горячего» и «холодного» спаев На рисунке 1 показана типичная схема включения термопары с нетермостатированным "холостым" контактом, когда температура Т2 равна температуре окружающей среды. Термо-ЭДС ε термопары в небольшом интервале температур пропорциональна разности температур спаев (1):
где α12 – коэффициент ТЭДС (величина ТЭДС возникающая при разности температур спаев в 1 К). Коэффициент ТЭДС α12 зависит от коэффициентов веществ электродов (2):
Коэффициенты ТЭДС различных веществ определяются по отношению к свинцу, для которого αPb = 0. Коэффициент ТЭДС может иметь как положительное, так и отрицательное значение и в общем случае зависит от температуры [1]. 1.2 Эффект Зеебека и влияние температуры на распределение Ферми-Дирака в собственных и примесных полупроводниках1) Эффект Зеебека объясняется тем, что средняя энергия электронов проводимости зависит от природы проводника и по-разному растёт с температурой. Если вдоль проводника существует градиент температур, то электроны на горячем конце приобретают более высокие энергии и скорости, чем на холодном. В полупроводниках в дополнение к этому концентрация электронов проводимости растёт с температурой. В результате возникает поток электронов от горячего конца к холодному и на холодном конце накапливается отрицательный заряд, а на горячем остаётся нескомпенсированный положительный заряд. Процесс накопления заряда продолжается до тех пор, пока возникшая разность потенциалов не вызовет поток электронов в обратном направлении, равный первичному, благодаря чему установится равновесие. Алгебраическая сумма таких разностей потенциалов в цепи создаёт одну из составляющих ТЭДС, которую называют объёмной. 2) Распределение Ферми-Дирака определяет статистическое распределение заряженных частиц по энергетическим уровням системы, находящейся в термодинамическом равновесии. В статистике Ферми-Дирака среднее число частиц в состоянии с энергией 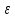 есть (3): есть (3):
где 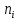 – среднее число частиц в состоянии – среднее число частиц в состоянии 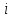 ; ;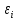 – энергия состояния – энергия состояния 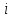 ; ;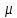 – химический потенциал (который равен – химический потенциал (который равен 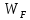 при абсолютном нуле при абсолютном нуле 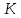 ); );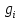 – число состояний с энергией – число состояний с энергией 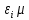 ; ;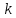 – постоянная Больцмана; – постоянная Больцмана;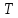 – абсолютная температура. – абсолютная температура.В идеальном случае (в ферми-газе) в пределе низких температур 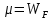 . В этом случае (полагая, что уровни энергии невырожденные, . В этом случае (полагая, что уровни энергии невырожденные, 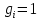 ), функция распределения частиц называется функцией Ферми (4): ), функция распределения частиц называется функцией Ферми (4):
В собственном полупроводнике положение уровня Ферми не зависит от температуры. Объясняется это тем, что процессы, определяющие проводимость собственного полупроводника, не меняют своего характера при изменении температуры. Конечно, с ростом температуры и увеличением энергии теплового возбуждения электроны будут переходить на всё более высокие уровни зоны проводимости, достаточно удаленные от её дна. Однако одновременно с этим тепловое возбуждение будет переводить в зону проводимости электроны, располагающиеся на наиболее глубоких уровнях валентной зоны. Поэтому средняя энергия носителей заряда, принимающих участие в проводимости, остается неизменной, и уровень Ферми в собственном полупроводнике независимо от температуры сохраняет своё положение в середине запрещённой зоны. Иная картина наблюдается в примесных полупроводниках. Уровень μ в донорном полупроводнике при низких температурах располагается в запрещенной зоне на расстоянии 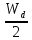 от дна зоны проводимости, а с ростом температуры на смену примесной проводимости приходит собственная проводимость. Это и является причиной изменения положения уровня μ. В области низких температур наличие у электронного полупроводника проводящих свойств обусловлено переходами электронов в зону проводимости с донорных уровней. Поэтому и уровень Ферми расположен посередине между примесным уровнем и дном зоны проводимости. По мере повышения температуры происходит, истощение примесей, а при от дна зоны проводимости, а с ростом температуры на смену примесной проводимости приходит собственная проводимость. Это и является причиной изменения положения уровня μ. В области низких температур наличие у электронного полупроводника проводящих свойств обусловлено переходами электронов в зону проводимости с донорных уровней. Поэтому и уровень Ферми расположен посередине между примесным уровнем и дном зоны проводимости. По мере повышения температуры происходит, истощение примесей, а при 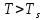 (температуре истощения, при которой все электроны с донорного уровня оказываются переведенными в зону проводимости) донорный уровень оказывается практически пустым. Но в этой области температур на смену переходам в зону проводимости с донорного уровня все в большей степени приходят переходы из валентной зоны – начинает проявляться собственная проводимость. При высоких температурах, когда (температуре истощения, при которой все электроны с донорного уровня оказываются переведенными в зону проводимости) донорный уровень оказывается практически пустым. Но в этой области температур на смену переходам в зону проводимости с донорного уровня все в большей степени приходят переходы из валентной зоны – начинает проявляться собственная проводимость. При высоких температурах, когда 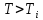 ( (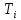 называется температурой перехода к собственной проводимости) проводимость полупроводника практически полностью определяется переходами электронов из валентной зоны, из-за чего и средняя энергия электронов проводимости становится равной называется температурой перехода к собственной проводимости) проводимость полупроводника практически полностью определяется переходами электронов из валентной зоны, из-за чего и средняя энергия электронов проводимости становится равной 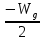 ( (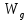 – энергия запрещённой зоны, а знак «минус» означает, что положительные значения энергии от дна зоны проводимости откладываются вверх). Уровень μ в этих условиях занимает положение в середине запрещенной зоны. Таким образом, по мере роста температуры уровень Ферми в электронном полупроводнике изменяет своё положение от – энергия запрещённой зоны, а знак «минус» означает, что положительные значения энергии от дна зоны проводимости откладываются вверх). Уровень μ в этих условиях занимает положение в середине запрещенной зоны. Таким образом, по мере роста температуры уровень Ферми в электронном полупроводнике изменяет своё положение от 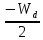 до до 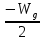 (рисунок 2). (рисунок 2).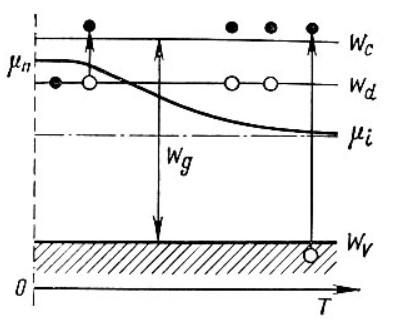 Рисунок 2 – Зависимость уровня Ферми от температуры 1.3 Влияние фононов и контактная разность потенциалов1) Фонон – квант колебательного движения атомов кристалла. Колебания атомов кристалла благодаря взаимодействию между ними распространяются по кристаллу в виде волн. Рассеяние электронов проводимости при взаимодействии с фононами – основной механизм электросопротивления металлов и полупроводников. В металлах концентрация электронов проводимости велика и не зависит от температуры. Энергия электронов также почти не зависит от температуры, поэтому ТЭДС металлов очень мала. Сравнительно больших значений достигает ТЭДС в полуметаллах и их сплавах, где концентрация носителей значительно меньше и зависит от температуры, а также в некоторых переходных металлах и их сплавах. В последнем случае концентрация электронов велика. Однако ТЭДС велика из-за того, что средняя энергия электронов проводимости сильно отличается от энергии Ферми. Иногда быстрые электроны обладают меньшей диффузионной способностью, чем медленные, и ТЭДС в соответствии с этим меняет знак. Величина и знак ТЭДС зависят также от формы поверхности Ферми. В термоэлементе, состоящем из дырочного и электронного полупроводников, ТЭДС складываются. В полупроводниках со смешанной проводимостью к холодному контакту диффундируют и электроны и дырки, и их заряды взаимно компенсируются. Если концентрации и подвижности электронов и дырок равны, то ТЭДС равна нулю. 2) Вторая (контактная) составляющая – следствие температурной зависимости контактной разности потенциалов. Если оба контакта термоэлемента находятся при одной и той же температуре, то контактная и объёмная ТЭДС исчезают. Контактная разность потенциалов – разность электрических потенциалов, возникающая между контактирующими телами в условиях термодинамического равновесия. Наиболее важно понятие к.р.п. для твёрдых проводников (металлов и полупроводников). Если два твёрдых проводника привести в соприкосновение, то между ними происходит обмен электронами, причём вначале преимущественно электроны переходят из проводника с меньшей работой выхода в проводник с большей работой выхода. В результате этого процесса проводники приобретают электрические заряды противоположных знаков, что приводит к появлению электрического поля, препятствующего дальнейшему перетеканию электронов. В конечном счёте, достигается равновесие, при котором потоки электронов в обоих направлениях становятся одинаковыми, и между проводниками устанавливается к.р.п. Электрическое поле к.р.п. сосредоточено в проводниках вблизи границы раздела и в зазоре между проводниками. Линейные размеры этой области порядка длины экранирования, которая тем больше, чем меньше концентрация электронов проводимости в проводнике. Длина экранирования в металлах имеет атомные размеры (10-8–10-7 см), а в полупроводниках колеблется в широких пределах и может достигать величины 10-4–10-5 см. Рассмотрим процесс образования контактной разности потенциалов металлов на основе зонной теории. На рисунке 3 показаны уровни Ферми и значения работы. Преимущественный переход электронов из металла 1 в металл 2 сопровождается изменением их потенциалов и соответствующим смещением энергетических уровней (по внешней шкале). Уровни металла 1, заряжающегося положительно, опускаются, а уровни металла 2, заряжающегося отрицательно, поднимаются. Изменение положения энергетических уровней будет происходить до тех пор, пока условия перехода электронов из одного металла в другой не окажутся одинаковыми. Так, для электронов, находящихся на уровнях Ферми, условие равновесия выражается равенством (5):
где 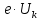 – работа, которую должен совершить электрон, идущий из металла 1 в металл 2, преодолевая к.р.п. – работа, которую должен совершить электрон, идущий из металла 1 в металл 2, преодолевая к.р.п. 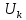 . .Равновесное состояние между металлами иллюстрирует рисунок 4. 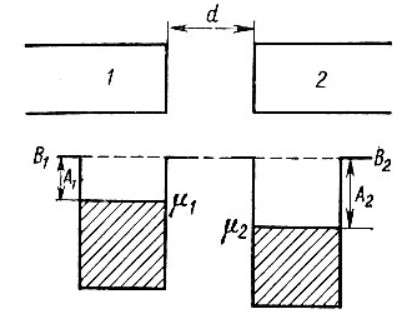 Рисунок 3 – Уровни Ферми в разных металлах 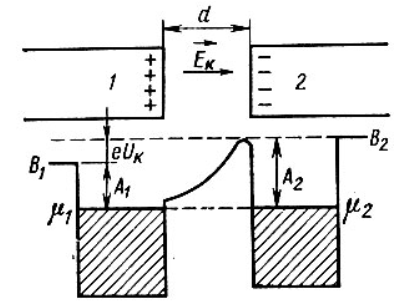 Рисунок 4 – Переход в равновесное энергетическое состояние Если до начала перехода электронов из металла 1 в металл 2 (рисунок 3) между уровнями Ферми разных металлов имеется некоторое энергетическое расстояние, то после установления статистического равновесия эти уровни оказываются одинаковыми (по внешней энергетической шкале). Значение к.р.п. равно разности работ выхода, отнесённой к заряду электрона. Отсюда следуют два вывода: 1) из двух соприкасающихся тел к.р.п. приходится в основном на проводники с большим сопротивлением; 2) для полупроводников в области сосредоточения к.р.п. заметно изменяется концентрация носителей заряда. К.р.п. даже при минимально возможном зазоре создаётся за счёт перехода с контактирующей поверхности одного материала на контактирующую поверхность другого порядка пары процентов свободных поверхностных электронов (разницы между числом свободных электронов, приходящихся на 1 см2 поверхности и перешедшими электронами). Именно поэтому контактное электрическое поле оказывается локализованным в контактном зазоре и почти не захватывает объемные области металлов. Если составить электрическую цепь из нескольких проводников, то к.р.п. между крайними проводниками определяется только их работами выхода и не зависит от промежуточных членов цепи (правило Вольта). К.р.п. может достигать величины в несколько вольт. Она зависит от строения проводника и от состояния его поверхности. Поэтому величина к.р.п. может быть изменена обработкой поверхностей (покрытиями, адсорбцией и т.п.), введением примесей (в случае полупроводников) и сплавлением с другими веществами (в случае металлов). 1.4 Диффузионный токПусть в полупроводнике концентрация электронов по мере удаления от внешней границы (которой на рисунке 5 соответствует координата x = 0) в глубину падает в соответствии с приведенной на этом рисунке кривой. Рассечем мысленно полупроводник в точке 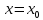 плоскостью, перпендикулярной оси Х и выделим из объёма два соседних слоя толщиной Δx. Все электроны, имевшиеся в слое 1 в некоторый начальный момент, в результате беспорядочного теплового движения через некоторое время покинут его. Поскольку вероятности движения электронов вправо и влево одинаковы, то можно считать, что половина электронов из слоя 1 перейдет через плоскость плоскостью, перпендикулярной оси Х и выделим из объёма два соседних слоя толщиной Δx. Все электроны, имевшиеся в слое 1 в некоторый начальный момент, в результате беспорядочного теплового движения через некоторое время покинут его. Поскольку вероятности движения электронов вправо и влево одинаковы, то можно считать, что половина электронов из слоя 1 перейдет через плоскость 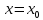 . В то же самое время половина электронов из слоя 2, имеющего такую же толщину Δx, пересечет эту плоскость в обратном направлении. Поскольку средняя концентрация электронов n1 в первом слое больше средней концентрации электронов n2 в слое 2, то число электронов, пересекающих границу раздела между слоями слева направо, будет больше числа электронов, идущих навстречу. Разность между этими потоками как раз и составит тот результирующий диффузионный поток, наличие которого и определяет появление диффузионного тока. . В то же самое время половина электронов из слоя 2, имеющего такую же толщину Δx, пересечет эту плоскость в обратном направлении. Поскольку средняя концентрация электронов n1 в первом слое больше средней концентрации электронов n2 в слое 2, то число электронов, пересекающих границу раздела между слоями слева направо, будет больше числа электронов, идущих навстречу. Разность между этими потоками как раз и составит тот результирующий диффузионный поток, наличие которого и определяет появление диффузионного тока.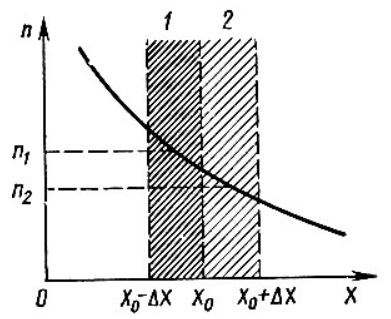 Рисунок 5 – Схематичное изображение двух слоёв полупроводника и распространения носителей заряда Диффузионный поток будет тем больше, чем больше различие между концентрациями электронов в контактирующих слоях. Разница же между n1 и n2 определяется значением изменения концентрации электронов на единице длины в направлении, перпендикулярном границе раздела между слоями 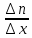 . Плотность электронного диффузионного тока можно выразить формулой (6): . Плотность электронного диффузионного тока можно выразить формулой (6):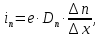 где 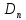 – коэффициент диффузии электронов. – коэффициент диффузии электронов.2 Практическая частьОборудование: песчаная баня, ртутный термометр, ЛАТР, термопара и мультиметр. Ход работы: 1. Подсоединить термопару к мультиметру и опустить конец со спаем в песчаную баню; 2. включить ЛАТР и выставить значение 100; 3. нагревая до 150°C с шагом в 5°C фиксируем ЭДС на мультиметре; 4. построить градуировочную кривую ЭДС от температуры; 5. найти чувствительность термопары и построить доверительный интервал. Результаты измерения приведены в таблице 1. Таблица 1 – Результаты измерения
Продолжение таблицы 1
На рисунке 6 приведена градуировочная кривая. 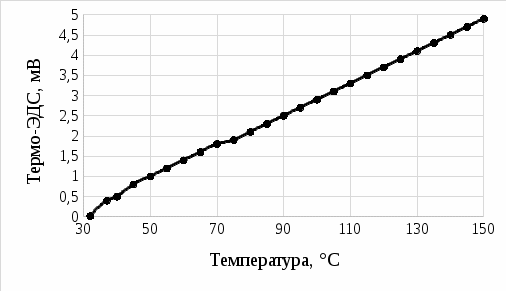 Рисунок 6 – Градуировочная кривая На рисунке 7 представлена рассчитанная чувствительность термопары. 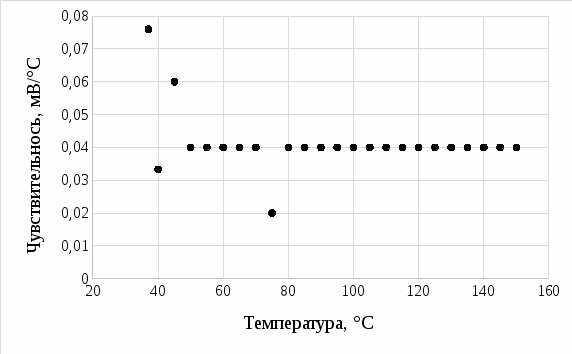 Рисунок 7 – Чувствительность термопары Чтобы найти доверительный интервал, необходимо найти среднее значение чувствительности. Среднее значение чувствительности равно 0,041. Рассчитаем стандартное отклонение (3):
Стандартное отклонение показывает, как распределены значения относительно среднего в выборке. Другими словами, можно понять, насколько велик разброс величины от измерения к измерению. Доверительный уровень равен 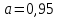 . Найдём величину . Найдём величину 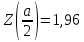 согласно стандартному распределению. Нормальное распределение – распределение вероятностей, которое задаётся распределением, совпадающим с функцией Гаусса, а стандартное нормальное распределение – нормальное распределение с математическим ожиданием равным нулю и стандартным отклонением равным единице. согласно стандартному распределению. Нормальное распределение – распределение вероятностей, которое задаётся распределением, совпадающим с функцией Гаусса, а стандартное нормальное распределение – нормальное распределение с математическим ожиданием равным нулю и стандартным отклонением равным единице. Найдём предел погрешности с помощью (4):
Итак, чувствительность равна 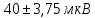 . .На рисунке 8 приведён график чувствительности термопары с доверительным интервалом. 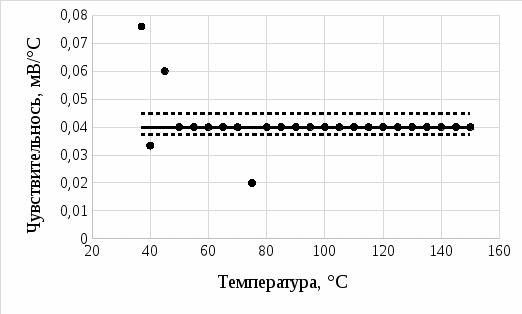 Рисунок 8 – Чувствительность термопары с доверительным интервалом Из рисунка 8 видно, что в доверительный интервал не вошли 4 значения, что, вероятно, является ошибками оператора. ЗАКЛЮЧЕНИЕВ ходе выполнения данной лабораторной работы была построена градуировочная кривая термопары по результатам измерений, рассчитан доверительный интервал, а также найдена чувствительность термопары. Чувствительность равна 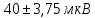 . Исходя из этого, были определены материалы термопары. Такую чувствительность может иметь термопара хромель-алюмель (ТХА) [4]. А также сплав хромель (90,5 % Ni + 9,5% Cr) и алюмель (94,5 % Ni + 5,5 % Al, Si, Mn, Co) [5]. . Исходя из этого, были определены материалы термопары. Такую чувствительность может иметь термопара хромель-алюмель (ТХА) [4]. А также сплав хромель (90,5 % Ni + 9,5% Cr) и алюмель (94,5 % Ni + 5,5 % Al, Si, Mn, Co) [5].СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ1 Термоэлектрические явления [Электронный ресурс] studfiles // [Электронный ресурс] : [сайт]. URL: https://studfiles.net/preview/4295216/page:2/ (дата обращения 3.02.2019) Загл. с экрана. Яз. рус. 2 Алёшкин, В. Я. Современная физика полупроводников: курс лекций / В. Я. Алёшкин. Н. Новгород: Изд-во ННГУ, 2013. 132 с. 3 Таблицы распределения [Электронный ресурс] statsoft // [Электронный ресурс] : [сайт]. URL: http://statsoft.ru/home/textbook/modules/sttable.html (дата обращения 3.02.2019) Загл. с экрана. Яз. рус. 4 Термопары. Типы, характеристики, конструкции, производство [Электронный ресурс] “Метотехника” // [Электронный ресурс] : [сайт]. URL: http://www.metotech.ru/art_termopary_4.htm (дата обращения 3.02.2019) Загл. с экрана. Яз. рус. 5 ГОСТ Р 8.585-2001. Государственная система обеспечения единства измерений (ГСИ). Термопары. Номинальные статические характеристики преобразования. М. : Стандартинформ, 2010. 81 с. |