школьный этап олимпиады по математики 7 класс. школьный этап олимпиады 7 класс. Школьный этап олимпиады по математике 20212022 учебный год
 Скачать 67.27 Kb. Скачать 67.27 Kb.
|
|
Школьный этап олимпиады по математике 2021-2022 учебный год 7 класс 1. Приведите пример двух обыкновенных дробей, разность которых в три раза больше их произведения. Приведите вычисления, обосновывающие это свойство. 2. Покажите, как разрезать фигуру на три части и сложить из них квадрат. 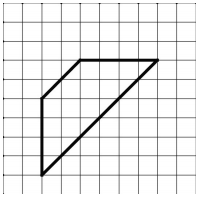 Рисунок к 2 заданию 3. На доске написано число 49. За один ход разрешается либо удваивать число, либо стирать его последнюю цифру. Можно ли за несколько ходов получить число 50? 4. Один из трёх друзей: Андрей, Борис или Владимир — самый сильный, другой — самый умный, третий — самый добрый. Однажды они сказали следующее: Андрей: Владимир сильнее меня. Борис: Я умнее Владимира. Владимир: Борис умнее меня. Известно, что самый сильный и самый добрый сказали правду, самый умный соврал и среди них нет двух людей, равных по силе. Верно ли, что среди трёх друзей тот, кто самый добрый, тот и самый слабый? Обоснуйте свой ответ. 5. Мама гуляет с коляской вокруг озера и полностью обходит озеро за 12 минут. Ваня по той же дорожке в ту же сторону ездит на самокате и встречает (обгоняет) маму каждые 12 минут. Через какие промежутки времени Ваня будет встречать маму, если он будет ездить с той же скоростью, но в обратном направлении? Школьный этап олимпиады по математике 2021-2022 учебный год 7 класс ОТВЕТЫ 1. (7 баллов) Приведите пример двух обыкновенных дробей, разность которых в три раза больше их произведения. Приведите вычисления, обосновывающие это свойство. Ответ. Например, 1/2 и 1/5 Решение Подходят любые дроби вида 1/n и 1/(n+3), есть и другие решения. Критерии проверки Любое полное верное решение — 7 баллов. Приведён верный ответ без обоснования — 3 балла. 2.(7 баллов) Покажите, как разрезать фигуру на три части и сложить из них квадрат.  Рисунок к 2 заданию Решение 1 способ 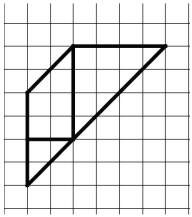 Рисунок 1 к решению 2 задания 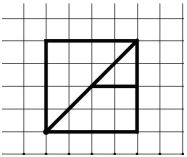 Рисунок 2 к решению 2 задания 2 способ 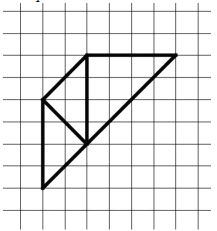 Рисунок 3 к решению 2 задания 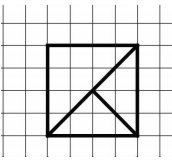 Рисунок 4 к решению 2 задания Возможны и другие решения. Критерии проверки. Любое верное решение (на рисунках показано, как разрезать трапецию и как складывать квадрат) — 7 баллов. Неполное решение (показано только, как разрезать трапецию или как сложить квадрат) — 3 балла. 3.(7 баллов) На доске написано число 49. За один ход разрешается либо удваивать число, либо стирать его последнюю цифру. Можно ли за несколько ходов получить число 50? Ответ. Можно. Решение Число 50 можно получить, удвоив 25, а 25 можно получить, стерев последнюю цифру числа 256, которое является степенью двойки. Таким образом, необходимая цепочка преобразований может выглядеть так: 49 → 4 → 8 → 16 → 32 → 64 → 128 → 256 → 25 → 50. Существуют и другие решения. Критерии проверки. Любое полное верное решение — 7 баллов. Неполное решение (например, указано, что 50 можно получить из числа 256, но не указано, как получить 256) — 3 балла. Приведён только ответ — 0 баллов. 4.(7 баллов) Один из трёх друзей: Андрей, Борис или Владимир — самый сильный, другой — самый умный, третий — самый добрый. Однажды они сказали следующее: Андрей: Владимир сильнее меня. Борис: Я умнее Владимира. Владимир: Борис умнее меня. Известно, что самый сильный и самый добрый сказали правду, самый умный соврал и среди них нет двух людей, равных по силе. Верно ли, что среди трёх друзей тот, кто самый добрый, тот и самый слабый? Обоснуйте свой ответ. Ответ. Да. Решение Обозначим: А — Андрей, Б — Борис, В — Владимир. Утверждения Б и В повторяют друг друга, а так как имеется только одно неверное утверждение среди трёх, Б и В сказали правду, А — ложь. Следовательно, А самый умный (по условию), А сильнее В (так как А соврал) и Б умнее В (так как Б и В сказали правду). Раз А сильнее В, то В не самый сильный. Получается, что самый сильный Б, средний по силе А, самый слабый — В. При этом В не самый умный и не самый сильный, значит, он самый добрый. Для наглядности можно занести имеющуюся информацию в таблицу. Будем обозначать «места» каждого качества: 1 — первое место (самый умный / сильный / добрый), 2 — среднее, 3 — последнее место.
Из таблицы видно, что В — самый добрый и самый слабый. Критерии проверки Любое полное верное решение — 7 баллов. Верно и обоснованно найдено, кто самый сильный, кто самый умный и кто самый добрый, а дальше продвижений нет — 5 баллов. Обоснованно получено, Андрей самый умный, верно распределены друзья по силе (все 3 места), но не получено или не соотнесено с тем, что Владимир самый добрый, — 5 баллов. Приведены рассуждения только для частного случая (например, рассмотрен только случай, что Андрей сказал неправду) без рассмотрения остальных частных случаев и без указания на их невозможность — 2 балла. Верный ответ с указанием, кто самый умный, кто самый сильный и кто самый добрый, с проведённой проверкой, что при такой расстановке все условия задачи выполнены, но без обоснований — 2 балла. В самом начале рассуждений допущена ошибка — 0 баллов. Приведён только ответ — 0 баллов. 5.(7 баллов) Мама гуляет с коляской вокруг озера и полностью обходит озеро за 12 минут. Ваня по той же дорожке в ту же сторону ездит на самокате и встречает (обгоняет) маму каждые 12 минут. Через какие промежутки времени Ваня будет встречать маму, если он будет ездить с той же скоростью, но в обратном направлении? Ответ. Через 4 минуты. Решение Так как мама полностью обходит озеро за 12 минут и встречает Ваню раз в 12 минут, за 12 минут Ваня проезжает вокруг озера ровно 2 раза, а мама — один. Значит, скорость Вани в 2 раза больше скорости мамы. Отсюда следует, что, когда Ваня ехал в том же направлении, что и мама, скорость их сближения была равна скорости мамы. Если Ваня будет ехать в противоположном направлении, то скорость их сближения будет равна трём скоростям мамы, то есть будет в три раза больше. Значит, он будет встречать маму в три раза чаще, то есть через каждые 4 минуты. Это рассуждение можно провести, введя обозначение для длины дорожки. Пусть a — длина дорожки вокруг озера (в метрах), тогда скорость мамы равна a/12 (м/мин), а скорость Вани — a/6 (м/мин). Скорость сближения в случае, если мама и Ваня едут навстречу друг другу равна 3a/12=a/4 (м/мин). Следовательно, с такой скоростью они преодолеют вместе a метров за 4 минуты, т. е. будут встречаться раз в 4 минуты. Критерии проверки Любое полное верное решение — 7 баллов. Верно найдено, что скорость Вани в 2 раза больше скорости мамы, верно найдена сумма скоростей, но окончательный вывод сделан неверно — 2 балла. Верно и обоснованно найдено, что скорость Вани в 2 раза больше скорости мамы, но дальнейшие рассуждения либо не обоснованы, либо не доведены до конца — 1 балл. Решение, в котором приведены конкретные расстояния и скорости и получен верный ответ, — 1 балл. Только верный ответ — 0 баллов. Максимальный балл за все выполненные задания — 35. |
