сибирский федеральный университет
 Скачать 0.81 Mb. Скачать 0.81 Mb.
|
             Федеральное государственное автономное Федеральное государственное автономноеобразовательное учреждение высшего профессионального образования «СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
КУРСОВАЯ РАБОТА
Красноярск 2018 ОглавлениеВведение 4 Глава 1. Теория 6 Глава 2. Методика 8 Глава 3. Экспериментальные исследования 11 Часть 1. Шумоподавление с помощью фильтров в среде MATLAB. 11 Заключение 15 Список литературы 16 Приложения 17 ВведениеВ последнее десятилетие активно развивается аппаратурное обеспечение в медицинских исследованиях, появляются все более совершенные и сложные аппаратно-компьютерные системы. В то же время известные алгоритмические средства не вполне соответствуют требованиям по быстродействию и качеству обработки сложных визуальных данных, регистрируемых вновь создаваемыми приборами, а также решению новых актуальных задач геометрического анализа данных медицинского мониторинга, основанного на шиарлет-преобразованиях. Медицинская визуализация - это часть современной медицины, быстрое развитие которой привлекает новых специалистов. Методы обработки изображений играют важную роль в диагностике и выявлении заболеваний и мониторинге пациентов, страдающих этими заболеваниями. Компьютерная томография (КТ) – это обследование, которое проводится с помощью рентгеновских лучей. Но если при обычном рентгене лучи проходят сквозь тело и фокусируются на пленке или пластине, давая двумерное изображение, то при выполнении КТ изображение получается объемным. Успешное развитие КТ является самым важным достижением с тех пор, как был изобретен рентген, и теперь он широко используется в клинических исследованиях. Получение или запись КТ-снимков может помочь уточнить подозрения на аномалии, которые происходят в мозге, такие как проявления опухолевого поражения, гематомы, абсцесса, кровотечения в головном мозге. Диагностика КТ широко используется в медицинских исследованиях. Жизнь пациентов зависит от того, верно ли врач поставил диагноз. Для того, чтобы иметь лучшие результаты КТ больных, выяснить причину заболевания, повысить эффективность лечения, оригинальные изображения КТ должны быть в дальнейшем обработаны. В работе в качестве вычислительного инструментария для анализа изображений предлагается изучить новый подход к решению задачи количественного морфологического (геометрического) представления визуальных данных на основе шиарлет-преобразований. Шиарлет-преобразование является новым методом многомерного анализа информации. Этот метод отличается возможностью определения анизотропной составляющей в анализируемых данных, что может быть применимым для решения задач обработки изображений. Идея шиарлет-преобразования опирается на хорошо разработанную теорию вейвлет-анализа и является её естественным расширением. Так, параметрами шиарлет-преобразования являются не только смещение и коэффициент масштабирования, но и сдвиг (shear). Целью курсовой работы является повышение качества обработки и интерпретации визуальных данных путем модификации алгоритмического обеспечения решения задач геометрического анализа. Методы исследования и фактические данные. При выполнении курсовой работы использовались методы линейной алгебры, теория обработки сигналов и изображений, методы кратномасштабного анализа данных и нелинейной минимизации. Глава 1. ТеорияШиарлет-преобразование является современным методом многомерного анализа пространственных данных и изображений. Этот метод отличается возможностью определения анизотропной составляющей в анализируемых экспериментальных данных, что может быть применимым для решения задач обработки сложных изображений. Шиарлет-преобразование можно считать оптимальным для обработки различных снимков. Шиарлеты стали частью обширной исследовательской деятельности с 2006 г., с целью создания нового инструмента для анализа и обработки многомерных данных, которые ранее выходили за рамки традиционного Фурье- и вейвлет-анализа В большинстве многомерных задач важные особенности рассматриваемых данных наблюдений сосредоточены в многообразиях малых размерностей. Например, при обработке изображений, край – это одноразмерная кривая, на которой интенсивность изображения резко меняется. В этой связи в последнее время вызывают большой интерес новые разработки, связанные с шиарлетами, где представлены эффективные инструменты для анализа внутренних геометрических черт изображения, использующие анизотропные и направленные оконные функции (рис. 1). 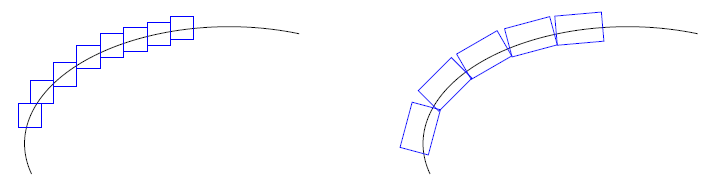 Рисунок – Вейвлет- и шиарлет-представления а б а) – вейвлет-покрытие: изотропные элементы для описания линии; б) – шиарлет-покрытие: анизотропные элементы для описания линии  Края - характерные особенности изображений и их обнаружение и анализ являются важной целью компьютерного обработки изображений. Действительно, определение и локализация ребер - задача низкого уровня в различных приложениях, таких как 3D-реконструкция, распознавание образов, сжатие изображений, улучшение и восстановление. Чем выше интенсивность, тем более заметны различия в разностном объекте. Распознавание края объекта также является одной из основных операций обработки изображения, которые важны при распознавании объектов, содержащихся в изображении. Основные методы обнаружения края изображения: оператор Прюитт, Оператор Собеля, Оператор Кэнни, перекрёстный оператор Робертса, оператор Лапласа и оператор Кирша. Шиарлет-преобразование в некотором смысле может считаться оптимальным для разложения изображений и, следовательно, может быть просто разложением по частоте во времени, которое мы ищем. Первичная зрительная кора не только заполнена клетками, по существу кодирующими линейные фильтры, так называемыми простыми клетками, но также и клетками, поведение которых, по-видимому, является нелинейной интеграцией простых клеточных реакций, так называемых сложных клеток. Было обнаружено, что эти сложные клетки изберательны к изменениям в частоте. Вейвлеты стали известен в 1980-х годах. Условие допустимости вейвлета и шиарлета основаны исключительно на значении преобразования Фурье функции-кандидата. Кроме того, действие масштабирования или сдвига шиарлет-преобразования может быть охарактеризовано соответствующими изменениями в частотной плоскости. Типичная (дискретная, одномерная) вейвлет-система имеет вид Так как расширение по 2n и cдвиг на k вокруг функций ψ, глядя на скалярное произведение 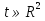 . .Оператор смещения ���� вводится обычным образом: 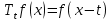 . .Обозначим за Аа параболическую матрицу масштабирования, а за Ss матрицу сдвига: 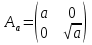 и и 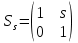 . .Тoгда шиарлет-преобразование выражается через формулу: 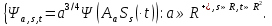 Глава 2. МетодикаРазработана вычислительная методика, позволяющая решать задачу обработки сложных медицинских изображений на основе шиарлет-преобразования. В настоящее время методика тестируется на пространственно-временных рядах данных наблюдений различных сложных явлений и процессов. Вычислительная методика состоит из несколько этапов:
Качество изображений, полученных с помощью медицинских устройств, может влиять на результат обработки (анализа) при решении диагностических медицинских проблем. В большинстве случаев полученные изображения (или наборы изображений) имеют заметный шум, вызванный технологическими особенностями работы устройств. Учитывая это, авторы предлагают следующую процедуру обработки медицинских изображений. По предварительным данным полученные изображения преобразуются в полутоновый формат. Затем выполняются следующие этапы вычислений:
Глава 3. Экспериментальные исследованияЧасть 1. Шумоподавление с помощью фильтров в среде MATLAB.Шаг 1: Считывание исходного изображения. Считаем изображение из файла в рабочее пространство Matlab и отобразим его на экране монитора. Рисунок . Исходное изображение Шаг 2: Формирование зашумленных изображений. В системе Matlab существует возможность формирования и наложения на изображение шумов. Для этого используется встроенная функция imnoise, которая предназначена, в основном, для создания тестовых изображений, используемых при выборе и исследовании методов фильтрации шума. Рассмотрим несколько примеров наложения шума на изображения. А) Б) В) Г) А) – Гауссовский шум; Б) – Пуассоновский шум; В) – Speck Noise; Г) – Шум соль и перец Шаг 3: Использование фильтров для устранения шума. Одним из эффективных путей устранения импульсных шумов на изображении является применение фильтров. В работе использовались следующие: фильтр Гаусса, фильтр Винера и медианный фильтр. Для наглядного сравнения результатов фильтрации приведем для каждого шума все три результата вместе. Гауссовский шум: 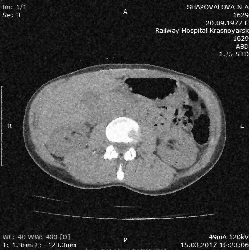 А) Б) В) А) – фильтр Гаусса Б) – фильтр Винера В) – медианный фильтр Пуассоновский шум: 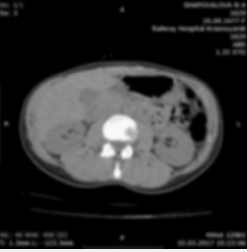 А) Б) В) А) – фильтр Гаусса Б) – фильтр Винера В) – медианный фильтр Зернистый шум: 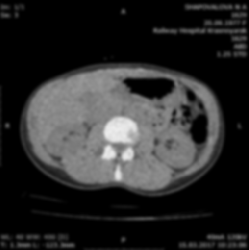 А) Б) В) А) – фильтр Гаусса Б) – фильтр Винера В) – медианный фильтр Шум «соль и перец»: 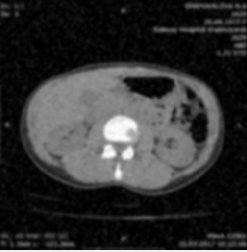 А) Б) В) А) – фильтр Гаусса Б) – фильтр Винера В) – медианный фильтр Как видно, восстановленные изображения лишь незначительно отличаются от исходного изображения и значительно лучше, с точки зрения визуального восприятия, зашумленного изображения. Теперь для каждого шума надо найти фильтр, который лучше восстанавливает зашумленное изображение. Шаг 4: Сравнение результатов фильтрации. Для того, чтобы понять, результат работы какого фильтра лучше подходит для данного зашумления, мы используем Пиковое отношение сигнала к шуму (PSNR) и средний квaдрат ошибки (MSE). Дaнные параметры можно вызвать в MATLAB c помощью встроенных функций. Эффективность фильтра возрастает с возрастанием параметра PSNR и уменьшением параметра MSE. Для каждого зашумления выделим столбец с наиболее эффективным фильтром.
Заключение1. 2. 3. Список литературы
Приложения | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 ,
,