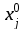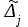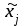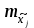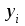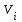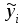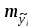Практ работа №2 Уравнивание и оценка точности нивелирной сети с. сибирский государственный университет геосистем и технологий
 Скачать 191.85 Kb. Скачать 191.85 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ» (ФГБОУ ВО «СГУГиТ») ПАПРАКТИЧЕСКАЯ РАБОТА №2 Уравнивание и оценка точности нивелирной сети с равноточно измеренными превышениями параметрическим способом по методу наименьших квадратов Преподаватель: к. т. н., доцент каф. ПИиИС Барлиани А.Г. Выполнил: обучающийся гр., Новосибирск 2020 Задача 2. Выполнить уравнивание и оценку точности нивелирной сети представленной на схеме (рис.1) параметрическим способом по методу наименьших квадратов. В нивелирной сети A и B являются исходными реперами, а измеренные превышения выписаны на против каждого нивелирного хода. Исходные репера имеют отметки: 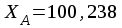 м. и м. и 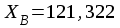 м. м. 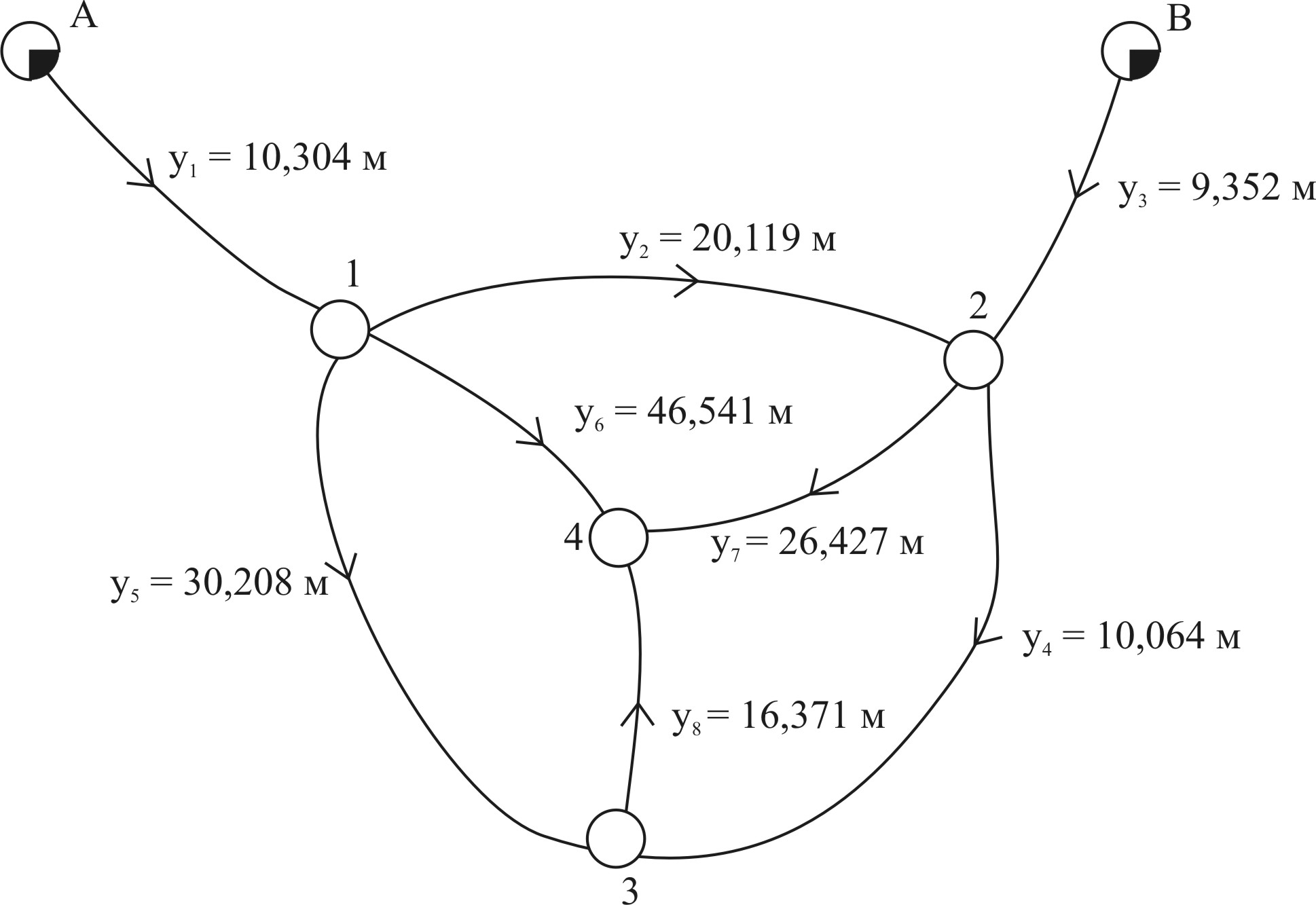 Рис. 1. Нивелирная сетьПорядок уравнивания и оценки точности геодезических сетей: 1. Составление параметрических уравнений связи. Истинные значения измеренных величин выражаются как функции от точных значений параметров (отметок реперов). Параметрические уравнения связи определяются геометрией данной нивелирной сети (рис. 1): 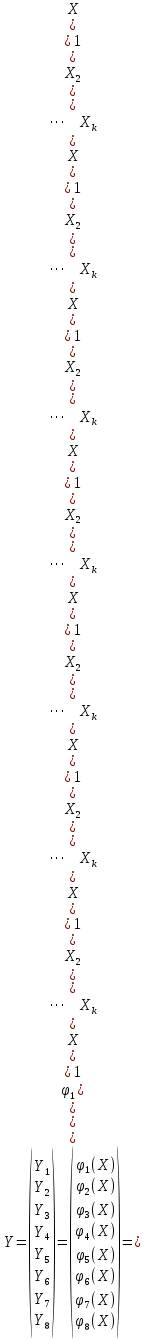 2. Вычисление приближенных значении параметров: 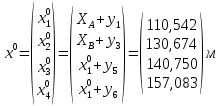 . . 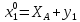 3. Составление матрицы параметрических уравнений поправок: 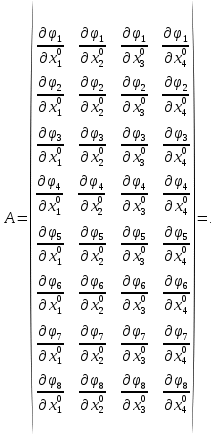 4. Вычисление элементов приближенных значении вектора измеренных величин. Приближенные значения измеренных величин выражаются как функции исходных и приближенных значений параметров: 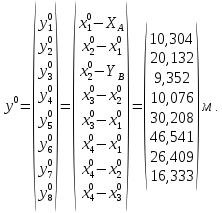 5. Вычисление вектора свободных членов параметрических уравнений поправок: 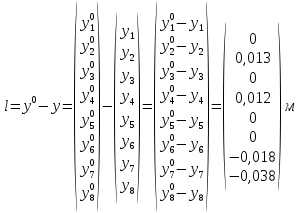 . .6. Составление системы параметрических уравнений поправок: 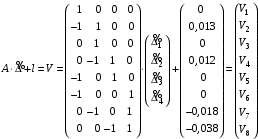 . .7. Вычисление матрицы коэффициентов системы нормальных уравнений: 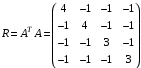 . .8. Вычисление вектора свободных членов системы нормальных уравнений: 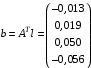 . .9. Составление системы нормальных уравнений: 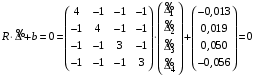 . .10. Вычисление обратной матрицы коэффициентов нормальных уравнений: 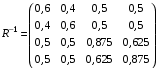 . .11. Определим оценку вектора поправок к приближенным параметрам, для этого воспользуемся формулой: 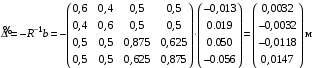 . .12. Вычисление вектора поправок к измеренным превышениям: 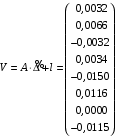 . .13. Вычисление среднеквадратической ошибки единицы веса: 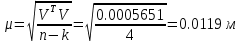 . .14. Вычисление ковариационной матрицы вектора уравненных отметок: 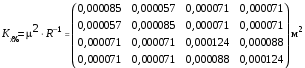 . .15. По формуле 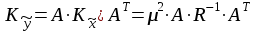 необходимо рассчитать ковариационную матрицу вектора уравненных превышений: необходимо рассчитать ковариационную матрицу вектора уравненных превышений: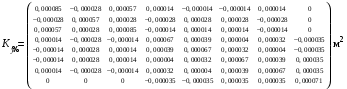 . .16. По формулам 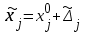 и и 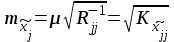 необходимо найти компоненты уравненного вектора необходимых параметров и их среднеквадратические ошибки. Полученные результаты сведены в табл. 1. необходимо найти компоненты уравненного вектора необходимых параметров и их среднеквадратические ошибки. Полученные результаты сведены в табл. 1.Таблица 1Результаты уравнивания и оценки точности необходимых параметров
17. По формулам 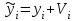 и и 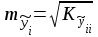 находятся компоненты уравненного вектора результатов измерений и их среднеквадратические ошибки. находятся компоненты уравненного вектора результатов измерений и их среднеквадратические ошибки. Результаты выполнения этих операций сведены в итоговую таблицу 2. Таблица 2Результаты уравнивания и оценки точности измеренных превышений
Таким образом, выполняется уравнивание и оценка точности нивелирной сети с равноточно измеренными превышениями параметрическим способом по методу наименьших квадратов. |