Курсовая работа по основам теории цепей. Сигналы (напряжения и токи) заданной полосы выделяют при помощи
 Скачать 0.73 Mb. Скачать 0.73 Mb.
|
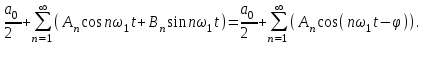 Где, 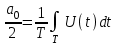 - постоянная составляющая; - постоянная составляющая;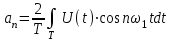 - амплитуда при синусах; - амплитуда при синусах;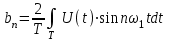 - амплитуда при косинусах; - амплитуда при косинусах;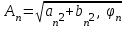 - амплитуда и фаза произвольной гармоники входного сигнала; - амплитуда и фаза произвольной гармоники входного сигнала;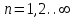 - номер гармоник; - номер гармоник;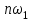 - частоты гармоник. - частоты гармоник.3.2. Анализ спектра Из теории высшей математики известно, что интеграл постоянной составляющей можно определить, как площадь под графиком, а также, что при разложении в ряд Фурье чётной функции у неё будут отсутствовать синусоидальные гармоники, а при разложении нечётной – косинусоидальные. Это вызвано тем, что по определению интегралы, как суммы, сводятся к 0 у симметричной нечётной функции, а интегралы симметричной чётной функции равны на каждой половине интегрируемого отрезка, т.е. их можно заменить удвоенным интегралом по половине отрезка. В таблице 4 приведены исходные данные к спектральному анализу входного сигнала. Таблица 4 – Свойства входного сигнала.
|
