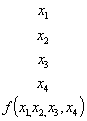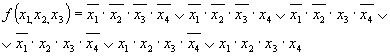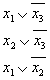Синтез компинационных устройств. Синтез комбинационных устройств. Синтез комбинационных устройств канонические формы представления логических функций
 Скачать 396.5 Kb.
|
Минимизация логических функций методом квайнаМетод Квайна относится к числу таких методов минимизации функции алгебры логики, которые позволяют представлять функции в ДНФ или КНФ с минимальным числом членов и минимальным числом букв в членах. Этот метод содержит два этапа преобразования выражения функции: на первом этапе осуществляется переход от канонической формы (СДНФ или СКНФ) к так называемой сокращенной форме, на втором этапе—переход от сокращенной формы логического выражения к минимальной форме. Первый этап (получение сокращенной формы). Пусть заданная функция f представлена в СДНФ. Переход к сокращенной форме основан на последовательном применении двух операций: операции склеивания и операции поглощения.    Для выполнения операции склеивания выявляются в выражении пары членов вида и , различающихся лишь тем, что один из аргументов в одном из членов представлен без инверсии, в другом—с инверсией. Затем проводится склеивание таких пар членов: , и резуль-таты склеивания w вводятся в выражение функции в качестве дополнительных членов. Далее проводится операция поглощения. Она основана на равенстве (член w поглощает член w? z). При проведении этой операции из логического выражения вычеркиваются все члены, поглощаемые членами, которые введены в результате проведения операции склеивания.Операции склеивания и поглощения проводятся последовательно до тех пор, пока их выполнение оказывается возможным. Покажем выполнение этих операций применительно к функции, представленной в табл. 3.5. Записываем СДНФ функции
Попарным сравнением членов (каждого из членов со всеми последующими) выявляем склеивающиеся пары членов:   первый и четвертый члены (результат склеивания ); второй и третий члены (результат склеивания ); второй и четвертый члены (результат склеивания ); третий и пятый члены (результат склеивания ):четвертый и пятый члены (результат склеивания ).
Результаты операции склеивания вводим в выражение функции и проводим операцию поглощения ими членов исходного выражения: Член поглощает те члены исходного выражения, которые содержат, т. е. первый и четвертый. Эти члены вычеркиваются. Член поглощает второй и третий, а член x1? x3 – пятый член исходного выражения.Повторяем операции склеивания и поглощения:  Член операции склеивания  Здесь склеивается лишь пара членов и , (склеивание пары членов и , приводит к тому же результату), результат склеивания х1, поглощает второй, третий, четвертый и пятый члены выражения.Дальнейшее проведение операций склеивания и поглощения оказывается невозможным, сокращенная форма выражения заданной функции (в данном примере она совпадает с минимальной формой)
Члены сокращенной формы (в рассмотренном примере такими членами служат и х1 называются простыми импликантами функции.Как видим, получено выражение существенно более простое по сравнению с СДНФ функции. На рис. 3.27 приведена структурная схема логического устройства в базисе И, ИЛИ, НЕ, построенная с использованием выражения (3.13). Второй этап (получение минимальной формы). Сокращенная форма может содержать лишние члены, исключение которых из выражения функции не повлияет на значение функции. Таким образом, дальнейшее упрощение логического выражения достигается исключением из выражения лишних членов. В этом и заключается содержание второго этапа минимизации. Покажем этот этап минимизации логического выражения на примере построения логического устройства для функции в табл. 3.6. 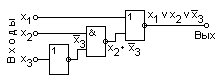 рис 3.27
Совершенная ДНФ.данной функции
Для получения сокращенной формы проводим операции склеивания и поглощения Полученное выражение представляет собой сокращенную форму логического выражения заданной функции, а члены его — простые импликанты функции. Переход от сокращенной формы к минимальной осуществляется с помощью импликантной матрицы, приведенной в табл. 3.7. В столбцы импликантной матрицы вписываются члены СДНФ заданной функции, в строки — простые импликанты функции, т. е. члены сокращенной формы логического выражения функции.
   Отмечаются (например, крестиками) столбцы членов СДНФ, поглощаемых отдельными простыми импликантами. В табл. 3.7 простая импликанта поглощает члены , , и в первом и во втором столбцах первой строки поставлены крестики; вторая импликанта поглощает первый и третий члены СДНФ, и поставлены крестики в первом и третьем столбцах второй строки и т. д. Импликанты, которые не могут быть лишними и, следовательно, не могут быть исключены из сокращенной формы, составляют ядро. Входящие в ядро импликанты легко определяются по импликантной матрице. Для каждой из них имеется хотя бы один столбец, перекрываемый только данной импликантой.  В рассматриваемом примере ядро составляют импликанты и, (только ими перекрываются второй и шестой столбцы матрицы). Исключение из сокращенной формы одновременно всех импликант, не входящих в ядро, невозможно, так как исключение одной из импликант может превратить другую уже в нелишний член. Для получения минимальной формы достаточно выбрать из импликант, не входящих в ядро, такое минимальное их число с минимальным количеством букв в каждой из этих импликант, которое обеспечит перекрытие всех столбцов импликантной матрицы, не перекрытых членами ядра. В рассматриваемом примере необходимо импликантами, не входящими в ядро, перекрыть третий и четвертый столбцы матрицы. Это может быть достигнуто различными способами, но так как необходимо выбирать минимальное число импликант, то, очевидно, для перекрытия этих столбцов следует выбрать импликанту . Минимальная дизъюнктивная нормальная форма (МДНФ) заданной функции
Структурная схема, соответствующая этому выражению, приведена на рис. 3.28. 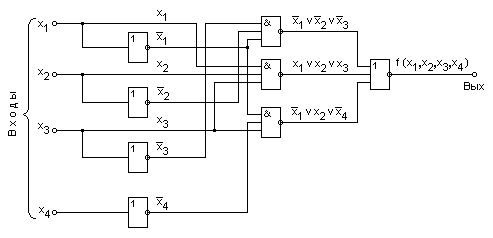 рис 3.28   Переход от сокращенной формы (3.15) к МДНФ (3.16) был осуществлен путем исключения лишних имплнкант и . Покажем допустимость подобного исключения членов из логического выражения. Импликанты и обращаются в единицу соответственно при следующих наборах значений аргументов: x1 = 0; х2 = 0; х3 = 0 и х2 = 1; х3 = 1; х4 = 0 (3.17)  Роль этих имликант в выражении сокращенной формы функции (3.15) заключается лишь в том, чтобы на приведенных наборах (3.17) значений аргументов присваивать функции значение 1. Однако при этих наборах функция имеет значение 1 из-за остальных импликант выражения (3.15). Действительно, подставляя значения (3.17) в (3.16), получаем:при x1 = 0, x2 = 0, x3 = 0   при х2 = 1; х3 = 1; х4 = 0 Таким образом, доказана справедливость операции исключения из выражения (3.15) членов и . До сих пор рассматривалось получение минимальной ДНФ. При использовании метода Квайна для получения минимальной конъюнктивной нормальной формы (МК.НФ) логической функции имеются следущие особенности:  исходной для минимизации формой логического выражения заданной функции является СКНФ; пары склеиваемых членов имеют вид и ; операция поглощения проводится в соответствии с выражениемРассмотрим применение метода Квайна на примере минимизации функции, заданной таблицей истинности (табл. 3.8). Совершенная КНФ рассматриваемой функции  Склеивающиеся пары членов: первый и третий члены (результат склеивания ); первый и четвертый члены (результат склеивания ):второй и третий члены (результат склеивания ).
Проводя операции склеивания и поглощения, получаем Члены операции склеивания Полученное выражение явлиется сокращенной формой функции. Для перехода к минимальной форме строим иммлнк.шгную матрицу (табл. 3.9). Все столбцы матрицы перекрываются импликантами и . Следовательно, член является лишним и минимальная конъюнктивная нормальная форма (МКНФ) заданной функции  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
