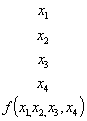Синтез компинационных устройств. Синтез комбинационных устройств. Синтез комбинационных устройств канонические формы представления логических функций
 Скачать 396.5 Kb. Скачать 396.5 Kb.
|
Синтез логических устройств в базисе ИЛИ_НЕ и И-НЕПостроение логического устройства на элементах ИЛИ-НЕ может быть выполнено при следующей последовательности действий: заданная функция минимизируется с получением МКНФ; производится запись полученного логического выражения через операции ИЛИ-НЕ. Рассмотрим последовательность синтеза на примере построения логического устройства, реализующего функцию, приведенную в табл. 3.28. Для минимизации функции воспользуемся методом Вейча. В табл. 3.29 приведена карта Вейча для рассматриваемой функции.
Минимальная КНФ функции Для перехода от базиса И, ИЛИ, НЕ, в котором представлено полученное логическое выражение, к базису ИЛИ-НЕ проводим следующие действия: дважды инвертируем правую часть выражении проводим преобразование по формуле де Моргана записываем выражение с использованием символа операции ИЛИ-НЕ Заметим, что в (3.18) наличие поставленных скобок обязательно, иначе исказится функция. Построенная в соответствии с (3.18) схема логического устройства приведена на рис. 3.32.  рис 3.32 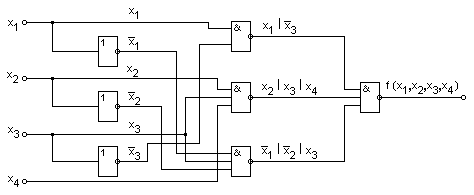 рис 3.33 Методика синтеза устройства в базисе И-НЕ сходна с рассмотренной выше методикой синтеза в базисе ИЛИ-НЕ. Имеющиеся особенности рассмотрим на примере построения с использованием элементов И-НЕ логического устройства, реализующего функцию, заданную таблицей истинности (табл. 3.28). Минимизируем функцию. В отличие от синтеза в базисе ИЛИ-НЕ, при котором в процессе минимизации получают МКНФ функции, при синтезе в базисе И-НЕ должна быть получена МДНФ функции. Минимизацию проведем с помощью карты Вейча (табл. 3.30). Минимальная ДНФ функции Дважды инвертируем правую часть выражения Проводим преобразование по формуле де Моргана Записываем выражение с использованием символа операции И-НЕ Выражению (3.20) соответствует схема, приведенная на рис. 3.33 Некоторые особенности построения схем логических устройствПостроенная структурная схема логического устройства может содержать элементы с разным числом входов. Так, в схеме на рис. 3.33 используются, кроме инверторов, элементы И-НЕ с двумя и тремя входами. В выпускаемых промышленностью сериях элементов обычно предусматриваются элементы с разным числом входов. Поэтому для построения устройств в большинстве случаев могут быть использованы элементы точно с тем же числом входов, какое требуется в отдельных элементах структурной схемы. Иногда по разным соображениям приходится использовать в схеме элементы, число входов у которых больше или меньше чем то, которое требуется при рассмотренных выше способах синтеза устройств. Ниже рассматриваются возникающие в этих случаях особенности построения устройств. Рассмотрим использование элементов, имеющих избыточное число входов. Для определенности примем, что элементы имеют три входа, причем для подачи входных переменных требуется лишь два входа. Избыточный вход мог бы быть оставлен свободным (не подключенным к каким-либо цепям), как это показано на рис. 3.34,а. Однако для уменьшения влияния наводимых на этот вход помех нежелательно неиспользуемый вход оставлять свободным. При этом возможны следующие способы его включения. Неиспользуемый вход может быть подключен к любому из используемых входов (рис. 3.34,б). Недостаток такого способа соединения состоит в следующем. Объединение входов приводит к тому, что к выходу источника входного сигнала (т. е. к выходу предыдущего элемента, с которого сигнал подается на вход данного элемента) оказывается подключенным большее число входов элемента. Такое возрастание нагрузки вызывает увеличение задержки распространения сигнала, снижение быстродействия элемента. Поэтому наиболее удачным следует считать способ, при котором на неиспользуемый вход подается логическая константа 0 или 1 (т. е. потенциал, соответствующий логической константе 0 либо 1). Такой способ соединения показан на рис. 3.34,в. Здесь на свободные входы элементов ИЛИ и ИЛИ-НЕ подается постоянный потенциал уровня, соответствующего лог. 0, а для элементов И и И-НЕ – потенциал уровня, соответствующего лог. 1. Теперь рассмотрим более сложный случай построения устройства на элементах с недостающим числом входов. 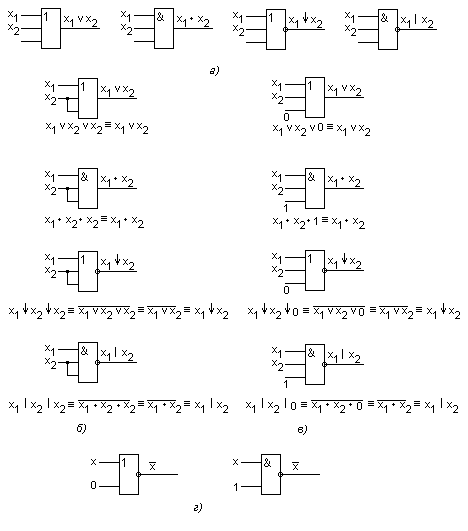 рис 3.34 На рис. 3.35 показан способ реализации 3х буквенного члена логического выражения функции на различных типах элементов с двумя входами.  рис 3.35 В логическом выражении может оказаться несколько членов с числом букв, превышающим число входов элементов. В этом случае для уменьшения числа используемых элементов следует провести соответствующее преобразование групп членов. Этот прием покажем на примере реализации рассмотренной выше логической функции (3.20). Пусть требуется построить устройстоо, реализующее функцию (3.20) на двухвходовых элементах И-НЕ. Обратимся к (3.19). В нем сгруппируем два последних члена, вынеся за скобки x3: 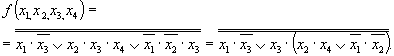 К полученному выражению применим формулу де Моргана Пользуясь формулой де Моргана, можно преобразовать к виду 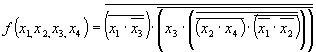 После подстановки в предыдущее выражение получим Запишем данное выражение через операцию И-НЕ: Построенная в соответствии с этим выражением схема приведена на рис. 3.36. Из сравнения схем ва рис. 3.33 и 3.36 видно, что синтез устройств на элементах с уменьшенным числом входов вызвал необходимость применения большего числа элементов. Изложенным приемом удается пользоваться не всегда. Например, им невозможно воспользоваться в случаях, когда члены МДНФ не содержат общих букв. При этом необходимое преобразование логического выражения достигается с использованием тождественного соотношения: Покажем справедливость этого тождества 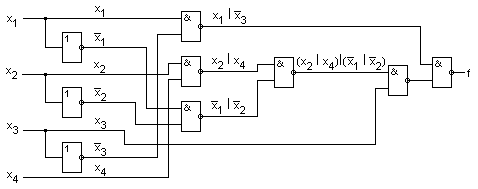 рис 3.36 Пусть требуется синтезировать с использованием двухвходо-вых элементов И-НЕ логическую функцию, МДНФ которой представляется выражением . Записываем выражение через операцию И-НЕ:  Применяя к данному выражению преобразование (3.21), получим Построенная в соответствии с данным выражением функциональная схема логического устройства приведена на рис. 3.37. Рассмотрим реализацию на двухвходовых элементах И-НЕ функции Перейдем к операции И-НЕ и затем применим соотношение (3.21): 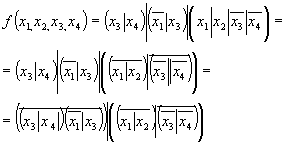 Аналогичное (3.21) преобразование для случая, когда предполагается реализация логического устройства в базисе ИЛИ-НЕ, имеет вид Покажем справедливость этого тождественного соотношения: 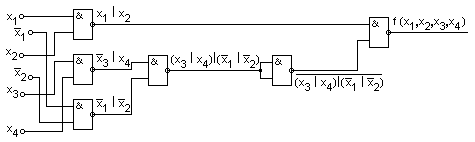 рис 3.37 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||