1. Метод наименьших квадратов алгоритм метода условия применения
 Скачать 281.01 Kb.
|
  1.Метод наименьших квадратов: алгоритм метода; условия применения. Для оценки параметров линейной или линеаризованной модели применяется метод наименьших квадратов (МНК). Суть метода состоит в следующем: к реальным данным подбирается функция и её параметры, чтобы разности (отклонения, остатки) между реальными и вычисленными значениями у были минимальны. Но разностей много, поэтому минимизируется сумма квадратов этих разностей: 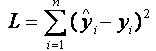 МНК с Поиском решения можно использовать непосредственно. Для этого надо задать произвольные коэффициенты a и b, построить по ним функцию Ŷ = a + bX, вычислить остатки e = Y – Ŷ и их квадраты, сумму e2. В окне Поиска решения установить Целевая ячейка ∑e2 минимум, Изменяя ячейки a и b, ограничений нет. Матричный метод МНК основан на представлении множеств X, Y, остатков E и параметров линейной модели B в виде векторов, над которыми затем проводятся операции. Векторное представление модели Y = B * X + E где Y B X E y1 1 x1e1 y2 1 x2e2 . a . . . b . . . . . yn 1 xnen Эту модель, записанную в векторном виде или в виде системы линейных уравнений, называют схемой Гаусса-Маркова. Условие МНК e2 - min , или в матричном виде (Y-XB)T(Y-XB) - min. Т означает транспонирование, то есть преобразование столбца в строку. Решением является вектор В: B = (XTX)-1XTY Здесь -1 означает обращение матрицы. Транспонирование и обращение матриц можно выполнять в Excel, используя функции ТРАНСП и МОБР. Согласно теореме Гаусса-Маркова, Метод наименьших квадратов, приведённый к линейному преобразованию матриц или к системе линейных уравнений, обеспечивает наилучшую несмещенную, эффективную и сходящуюся к пределу (“состоятельную”) оценку вектора параметров, т.е. наилучшее качество линейной модели, если соблюдаются условия:
5. Равенство ожидаемых значений дисперсий возмущений в разных диапазонах Х: E(u2)= Const. Это свойство называется гомоскедастичность, его несоблюдние – гетероскедастичность. 2.Типы переменных в эконометрических моделях. Структурная и приведённая формы спецификации эконометрических моделей. Основные виды переменных в эконометрике: - эндогенные, или зависимые переменные, прогнозирование которых является одной из основных задач эконометрики; - экзогенные, или влияющие переменные; могут быть внешними по отношению к системе (курс доллара, учетная ставка, время), или мы можем ими управлять: расходы на разные цели; - лаговые: переменные прошедших временных интервалов; вчера мы пытались их прогнозировать, а сегодня знаем. Экзогенные и лаговые объединяют термином предопределённые.Кроме того, существуют фиктивные, замещающие, инструментальные переменные Для построения прогнозов эндогенных переменных необходимо выразить текущие эндогенные переменные модели в виде явных функ ций предопределённых переменных. Последняя спецификация, полученная путем включе ния случайных возмущений получена в результате математической формализации экономических закономер ностей. Такая форма спецификации называется структурной. В общем случае в структурной спецификации эндогенные переменные не выра жены в явном виде через предопределенные. Модель, в которой эндогенные переменные выражены в явном виде через предопределенные переменные получила название приведенной. В частном случае структурная и приведённая фор мы модели могут совпадать. При правильной спецификации модели пере ход от структурной к приведённой форме всегда возможен, обратный пе реход возможен не всегда. Введем следующие обозначения:
С учетом данных обозначений матричная запись структурной формы эконометрической модели принимает вид AYt +BXt=Vt. Матричное представление приведённой формы спецификации сле дующее: Yt=MXt+Ut, где М— матрица приведенных коэффициентов, то есть М = –А-1 В. 3. Статистические свойства оценок параметров парной регрессионной модели Коэффициенты линейного уравнения регрессии bi имеют экономический смысл: это предельные функции, или производные эндогенной переменной по влияющим: 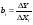 В случае парной регрессии это однозначно, в множественной регрессии всё сложнее из-за взаимного влияния регрессоров. Для оценки погрешностей коэффициентов уравнения парной линейной регрессии Ŷ= a + bx используются выражения   где S – выборочные оценки стандартных отклонений . Для принятия гипотезы о влиянии регрессора на эндогенную переменную используются таблицы критических значений t-статистики Стьюдента. Для bt=b/Sb . Предполагается, что при числе измерений больше 20 истинные значения коэффициентов уравнения регрессии и лежат в интервалах {a-2Sa , b+2 Sb } и {b-2Sb , b+2 Sa } с доверительной вероятностью 95%. 4. Этапы построения эконометрических моделей. 1. Постановка задачи. Необходимо понять потребности, сформулировать цель работы, предполагаемые результаты, имеющиеся ресурсы (денежные, технические, кадровые, юридические), объем работ, который предполагается выполнить; оценить имеющиеся разработки и программное обеспечение, стоимость закупки или разработки недостающего; решить вопрос о целесообразности разработки; разработать техническое задание, календарный план, соглашение о цене. 2. Обследование предметной области, сбор и оценка качества информации. От качества исходной информации об объекте моделирования зависят как адекватность модели, так и достоверность результатов моделирования. В эконометрических исследованиях данные разбиваются на три группы: cross-sectionaldata, в российских учебниках обозначаются как “пространственные”; временные ряды (timeseries); paneldata, в российских учебниках “панельные”, содержащие набор временных рядов. 3. Построение концептуальной модели: В зависимости от характера изучаемых процессов в системе все виды моделирования могут быть разделены на детерминированные и стохастические, статические и динамические, дискретные, непрерывные и дискретно-непрерывные. Детерминированное моделирование отображает детерминированные процессы, т.е. процессы, в которых предполагается отсутствие всяких случайных воздействий; стохастическое моделирование отображает вероятностные процессы и события; эконометрическое моделирование относится к этому виду. В этом случае анализируется ряд реализаций случайного процесса и оцениваются средние характеристики, т.е. набор однородных реализаций. Статическое моделирование служит для описания поведения объекта в какой-либо момент времени, в эконометрике такие модели называют пространственными. Динамическое моделирование отражает поведение объекта во времени. В эконометрике изучают временные ряды и их наборы (панельные данные). Дискретное моделирование служит для описания процессов, которые предполагаются дискретными, соответственно непрерывное моделирование позволяет отразить непрерывные процессы в системах, а дискретно-непрерывное моделирование используется для тех случаев, когда хотят выделить наличие как дискретных, так и непрерывных процессов. Эконометрика базируется на дискретных данных, но результатом является непрерывная функция. Основные этапы построения концептуальной модели: выдвижение гипотез и предложений; определение параметров и переменных модели; обоснование выбора показателей и критериев эффективности системы; составление содержательного описания модели. Выбранные показатели и критерии эффективности системы должны отражать цель функционирования системы и представлять собой функции переменных и параметров системы. Основные виды переменных в эконометрике: эндогенные, или зависимые переменные, прогнозирование которых является одной из основных задач эконометрики; экзогенные, или влияющие переменные; могут быть внешними по отношению к системе (курс доллара, учетная ставка, время), или мы можем ими управлять: расходы на разные цели; лаговые: переменные прошедших временных интервалов; вчера мы пытались их прогнозировать, а сегодня знаем. 4. Формальное описание задач, построение структурной модели: системы уравнений, тождеств, ограничений-равенств и ограничений-неравенств. 5. Разработка алгоритма решения задачи. Алгоритм – это конечная последовательность точно определенных действий, однозначно определяющая процесс преобразования исходных и промежуточных данных, приводящий к решению задачи. В эконометрике – это преобразование структурной модели к приведённой форме: уравнению или системе равенств, в которых эндогенные (прогнозируемые) переменные будут в левой части, а экзогенные и лаговые – в правой. Этот этап требует большого количества вычислений. В настоящее время многие программы для решения таких задач оформлены в виде сервисов различных прикладных пакетов: Excel, MatCad, MatLab, Stata, EViews и др., решение задачи обычно заменяется выбором пакета, сервиса, его настройкой и стыковкой с используемыми данными, обычно в интерактивном графическом режиме: ввод формул, установка ограничений и т.д. 6. Тестирование. Как отдельные блоки, так и программа в целом должны быть проверены с помощью тестовых задач с известными решениями. 90% эконометрики – это методы оценки надёжности модели в целом и её параметров. Показатели качества эконометрической модели: коэффициент детерминации R2, статистика Фишера F, t-статистики Стьюдента для коэффициентов уравнений, тест Дарбина-Уотсона на автокорреляцию DW, тест Голдфелда-Квандта на гетероскедастичность GQ, выявление мультиколлинеарности по матрице корреляции экзогенных переменных, а также оценка погрешности прогноза и проверка адекватности модели. 7. Оформление и интерпретация результатов моделирования имеет целью переход от информации, полученной в результате машинного эксперимента с моделью, к выводам, касающимся процесса функционирования объекта-оригинала. Результаты моделирования могут быть представлены в виде таблиц, графиков, диаграмм, схем и т.п. 5.Порядок оценивания линейной эконометрической модели из изолированного уравнения в Excel. Смысл выходной статистической информации сервиса Регрессия. (10) стр 41 Ещё больше информации даёт сервис Регрессия из Пакета анализа Excel. Для его запуска надо щелкнуть в Меню Excel 2003 Сервис – Анализ данных – Регрессия. (Если Анализ данных в меню Сервиса не появится, щелкните Надстройки и установите флажок Пакет анализа). В Excel 2007 и 2010 Пакет анализа вызывается в разделе Меню Данные. Если Анализ данных не виден, установить его: Файл – Параметры – Надстройки – Параметры Excel применить – Пакет анализа. Укажите диапазоны ячеек Y и X и на какой лист выводить результаты – на новый или на тот же. В этом случае надо указать достаточно большой диапазон ячеек для вывода. Поставьте флажок Метка, если выделили X и Y с заголовками. Сервис Регрессия выводит все статистические характеристики модели с соответствующими надписями. Сервис Регрессия может применяться для линейных или линеаризованных моделей. Стандартные надписи и дополнительные пояснения позволяют быстро разобраться в таблице результатов сервиса Регрессия. Сервис Регрессия можно применять к линеаризованным моделям, а также считая х в разных степенях в полиноме как самостоятельные экзогенные переменные, то есть сводя полиномиальную модель к модели множественной регрессии. 6.Спецификация и оценивание МНК эконометрических моделей нелинейных по параметрам. (30) стр.24-25, Для оценки параметров линейной или линеаризованной модели применяется метод наименьших квадратов (МНК). Суть метода: к реальным данным подбирается функция и её параметры, чтобы разности (отклонения, остатки) между реальными и вычисленными значениями у были минимальны. Но разностей много, поэтому минимизируется сумма квадратов этих разностей: 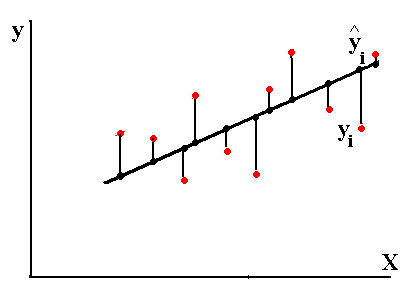 Рис.Отклонения реальных у от оценённой функции регрессииРассмотрим технологию МНК, которая используется ручном вычислении параметров парной линейной регрессии. Сумма квадратов остатков, зависящая от параметров a и b 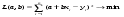 где n – количество измерений. Эта функция достигает минимума в точке, где её частные производные по a и по bравны нулю: an + bx = y ax + bx2 =xy Это называется система нормальных уравнений. В ней два уравнения и два неизвестных aи b, а коэффициенты получаются суммированием х, у и т.д. В моделях, нелинейных по параметрам, например степенных или показательных, непосредственное применение МНК для их оценки невозможно, так как необходимым условием применимости МНК является линейность по коэффициентам уравнения регрессии. В данном случае преобразованием, которое приводит уравнение регрессии к линейному виду, является логарифмирование. Логарифмические модели: 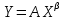 , где А и β— параметры модели. Прологарифмируем обе части данного уравнения: ln(Y)=ln(A) + β*ln(X) = α+β*ln(X), где α= ln(A) (*). Спецификация, соответствующая (*) называется двойной логарифмической моделью: ln(Y)= α+β*ln(X)+ε, поскольку и эндогенная переменная, и регрессор используются в логарифмической форме. Введем обозначения: 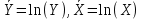 . Получаем спецификацию линейной модели, к которой при соответствующем включении случайного возмущения применим МНК.Нелинейный МНК. В общем случае оценка нелинейных по параметрам уравнений выполняется с помощью так называемого нелинейного метода наименьших квадратов (НМНК). Обозначим нелинейное по параметрам уравнение регрессии f(X, ß) (X— матрица рсгрсссоров,ß — вектор параметров). Параметры уравнений в данном методе подбираются таким образом, чтобы максимально приблизить кривую f(X, ß) к результатам наблюдений эндогенной переменной Y. Таким образом, здесь, как и в обычном МНК, минимизируется сумма квадратов отклонений: F= 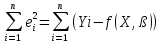 2 (**)Если продифференцировать F по параметрам и приравнять производные нулю, то получим нелинейную систему нормальных уравнений. В случае линейного уравнения регрессии нормальные уравнения представляли собой систему линейных уравнений, решение которой не составляло труда. Нелинейный метод наименьших квадратов сводится к задаче минимизации функции (**) нескольких переменных ß=(ß1,…,ßn) 7. Классическая парная регресионная модель. Спецификация модели. Теорема Гаусса-Маркова. Простая (парная) регрессия представляет собой модель, где ожидаемое значение зависимой (объясняемой, эндогенной) переменной y рассматривается как функция одной объясняющей (независимой или управляемой, предопределённой) переменной х, то есть модель вида Е(y) =f(x) Регрессионные модели, которые наиболее часто используются в эконометрике: 1) Линейная y = a + bx+u; употребляется наиболее часто, остальные функции стараются преобразовать к линейному виду, линеаризовать. Регрессии, нелинейные относительно включённых в анализ объясняющих переменных: 2) Полином второй, редко третьей степени y = a + bx+сх2+u. 3) Равносторонняя гипербола y = a +b/x +u. Эти модели сводятся к линейным заменой переменных: z = х2 для полинома и z=1/x для гиперболы. К нелинейным регрессиям по оцениваемым параметрам относятся: 4) Степенная y = axb; 5) Показательная y = abx; 6) Экспоненциальная y = ea+bx. Согласно теореме Гаусса-Маркова, Метод наименьших квадратов, приведённый к линейному преобразованию матриц или к системе линейных уравнений, обеспечивает наилучшую несмещенную, эффективную и сходящуюся к пределу (“состоятельную”) оценку вектора параметров, т.е. наилучшее качество линейной модели, если соблюдаются условия (по [ 1 ]):
5. Равенство ожидаемых значений дисперсий возмущений в разных диапазонах Х: E(u2)= Const. Это свойство называется гомоскедастичность, его несоблюдние – гетероскедастичность. Отклонение от гомоскедастичности проверяется по тесту Голдфелда-Квандта GQ = e12/e22 где e12 и e22 – суммы квадратов остатков (отклонений) в первой и последней трети (или в половинах) диапазона Х; большая сумма делится на меньшую!!!; GQ сравнивают с критерием Фишера для заданных уровня значимости и количества измерений; гипотеза о гомоскедастичности принимается при GQ <4,35. 6. Отсутствие автокорреляции, т.е. взаимозависимости возмущений. Её оценивают, вычисляя статистику Дарбина-Уотсона остатков е: 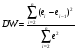 для которой вычислены критические значения при различных уровнях значимости и числе измерений. Приблизительно DW=0…1 означает положительную автокорреляцию, 3…4 отрицательную автокорреляцию, DW=1,5…2,5 позволяет принять гипотезу об отсутствии автокорреляции, DW=1…1,5 и DW=2,5…3 не позволяют принять гипотезу о наличии или отсутствии автокорреляции. Наличие автокорреляции означает, что аппроксимирующая функция подобрана неверно, или же требуется применение других методов и моделей. Автокорреляция разобрана в главе 8. Статистику Дарбина-Уотсона можно вычислить по формуле DW = 2(1-Rавт), где Rавт - коффициент автокорреляции, вычисляемый с помощью функции КОРРЕЛ: задать в окне Массив1 диапазон остатков с номерами 1 : n-1, а в окне Массив2 диапазон 2 : n. Понятия “гетероскедастичность” и “автокорреляция” актуальны, если массивы данных упорядочены, что имеет место для временных рядов. “Пространственные” данные можно искусственно упорядочить, например, отсортировав их по возрастанию какой-либо переменной; при этом можно выявить кластеры с аномальной дисперсией остатков, что может означать неоднородность выборки или неадекватность модели. Считается, что гетероскедастичность может привести к снижению эффективности оценок коэффициентов, и надо её искусственно подавлять: делить остатки в таблице 3.3 на их стандартные отклонения в диапазонах, а затем минимизировать сумму их квадратов. Эта технология называется Взвешенный метод наименьших квадратов (ВМНК) и обычно используется в матричном варианте МНК (раздел 3.3). При обнаружении автокорреляции остатков применяется Обобщённый метод наименьших квадратов ОМНК, основанный на преобразовании матриц, но с учётом корреляций остатков. 8. Метод наименьших квадратов: алгоритм метода, условия применения. Для оценки параметров линейной или линеаризованной модели применяется метод наименьших квадратов (МНК). Суть метода состоит в следующем: к реальным данным подбирается функция и её параметры, чтобы разности (отклонения, остатки) между реальными и вычисленными значениями у были минимальны. Но разностей много, поэтому минимизируется сумма квадратов этих разностей: 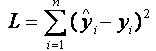Рис.3.1. Отклонения реальных у от оценённой функции регрессии. Как правило, вычисления проводятся на компьютере с использованием различных сервисов и программ. Далее мы рассмотрим технологию МНК, которую использовали при ручном вычислении параметров парной линейной регрессии. Сумма квадратов остатков, зависящая от параметров a и b 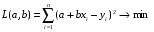 где n – количество измерений. Эта функция достигает минимума в точке, где её частные производные по a и по bравны нулю: 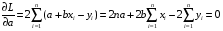 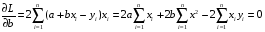 или an + bx = y ax + bx2 =xy 9.Идентификация отдельных уравнений системы одновременных уравнений: порядковое условие. (30) |