1. Метод наименьших квадратов алгоритм метода условия применения
 Скачать 281.01 Kb. Скачать 281.01 Kb.
|
|
Коэффициент уравнения называется идентифицируемым, если его можно вычислить на основе приведенных коэффициентов, причем точно идентифицируемым, если он единственный, и сверхидентифицируемым, если он имеет несколько разных оценок. В противном случае он называется неидентифицируемым. Какое-либо структурное уравнение является идентифицируемым, если идентифицируемы все его коэффициенты. Если хотя бы один структурный коэффициент неидентифицируем, то и все уравнение является неидентифицируемым. Модельсчитается идентифицируемой, если каждое ее уравнение идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель неидентифицируема. Уравнение структурной модели может быть идентифицируемо, если выполняется порядковое условие. Общий вид каждого уравнения модели в структурной форме можно записать как: (2.4) где: G – количество эндогенных переменных в модели K – количество предопределенных переменных в модели Необходимое условие идентифицируемости Теорема 1. Пусть i-ое поведенческое уравнение модели (2.4) идентифицируемо. Тогда справедливо неравенство Mi (пред) G – Mi (энд) – 1. (2.5) В нём: Mi (пред) – количество предопределённых переменных модели, не включённых в i-ое уравнение; Mi (энд)– количество эндогенных переменных модели, не включённыхв i-ое уравнение. Замечание. Справедливость неравенства (2.5) является необходимым условием идентифицируемости i-го уравнения. Это значит, что, когда неравенство (2.5) несправедливо, то i-ое уравнение заведомо неидентифицируемо. Однако при выполнении неравенства (2.5) ещё нельзя сделать вывод о идентифицируемости данного уравнения Условие (2.5), именуемое правилом порядка, позволяет выявлять неидентифицируемые уравнения модели, но не даёт возможности отмечать её идентифицируемые уравнения Определение неидентифицируемых уравнений производится методом «от противного»: если условие (2.5) не выполняется для i-го уравнения, то оно неидентифицируемо. 10.Оценка параметров парной регрессионной модели методом наименьших квадратов. (10) Для оценки параметров линейной или линеаризованной модели применяется метод наименьших квадратов (МНК). Суть метода состоит в следующем: к реальным данным подбирается функция и её параметры, чтобы разности (отклонения, остатки) между реальными и вычисленными значениями у были минимальны. Но разностей много, поэтому минимизируется сумма квадратов этих разностей: 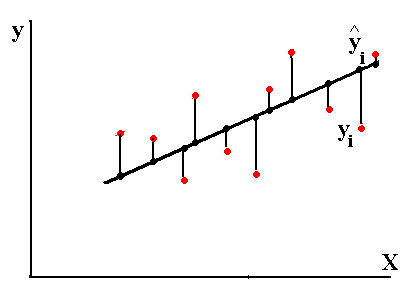 Рис.3.1. Отклонения реальных у от оценённой функции регрессии. Как правило, вычисления проводятся на компьютере с использованием различных сервисов и программ. Далее мы рассмотрим технологию МНК, которую использовали при ручном вычислении параметров парной линейной регрессии. Сумма квадратов остатков, зависящая от параметров a и b 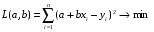 где n – количество измерений. Эта функция достигает минимума в точке, где её частные производные по a и по bравны нулю: 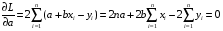 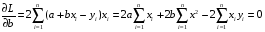 или an + bx = y ax + bx2 =xy Это называется система нормальных уравнений. В ней два уравнения и два неизвестных aи b, а коэффициенты получаются суммированием х, у и т.д. Решать её можно разными способами. В данном случае использован сервис Excel Поиск решения для настройки линейной модели по данным X и Y, представленным в Таблице 3.1. Коэффициенты системы нормальных уравнений расположены в виде матрицы (верхние строки таблицы 3.2), неизвестные a и b задаются произвольно и умножаются на коэффициенты (нижние строки). В окне Поиска решения задаются: Целевая ячейка – первая сумма, Значение равно 247 (y), Изменяя ячейки – a и b, Ограничения: вторая сумма равна 3901 (xy). Исходные данные X и Y приведены в Таблице 3.1. результаты расчёта в Таблице 3.2. Таблица 3.1. Таблица 3.2.
Теперь можно построить функцию регрессии Ŷ, сравнить её с Y и использовать для прогноза. В принципе, МНК с Поиском решения можно использовать непосредственно. Для этого надо задать произвольные коэффициенты a и b, построить по ним функцию Ŷ = a + bX, вычислить остатки e = Y – Ŷи их квадраты, сумму e2. В окне Поиска решения установить Целевая ячейка e2 минимум, Изменяя ячейки a и b, ограничений нет. Таблица 3.3.
11.Фиктивные переменные: определение, назначение, типы. В некоторых случаях, при повышении качества моделей, возникает необходимость оценки влияния качественных признаков на эндогенную переменную (пр.: для ф-ии спроса – это вкус потребителя, возраст, сезонность...). Эти показатели нельзя представить в численном виде. Поэтому используют фиктивные переменные – переем-е с дискретным множеством значений, которые образом описывают качественные признаки. Обычно используются фиктивные переменные бинарного типа «О—1»: В общем случае, когда качественный признак имеет более двух значений, вводится несколько бинарных переменных. При использовании нескольких бинарных переменных необходимо исключить линейную зависимость между переменными, так как в противном случае, при оценке параметров, это приведет к полной мультиколлинеарности. Поэтому применяется следующее правило: если качественная переменная имеет к альтернативных значений, то при моделировании используются только к-1 фиктивная переменная. Фиктивные переменные позволяют объединить в одной модели выборки, имеющие отличия. В принципе, их можно рассматривать отдельно, но объединение может дать более качественную модель. Повышение качества модели можно оценить, используя тест Чоу. Если при проведении статистических исследований какую-либо переменную сложно или невозможно измерить, но существует и известна её зависимость от другой, доступной переменной, то применяются замещающие (proxy) переменные: измеряют доступную переменную, строят с ней регрессионную модель, а затем прогнозируют значения недоступной переменной. Конечно, точность прогноза падает, но в некоторых случаях иначе не получается. В регрессионных моделях применяются фиктивные переменные двух типов: переменные сдвига и переменные наклона. 12.Автокорреляция случайного возмущения. Причины. Последствия. Модель называется автокоррелированной, если не выполняется третья предпосылка теоремы Гаусса-Маркова: Cov(ui,uj)≠0 при i≠j. Те между ними есть зависимость. Согласно теореме Гаусса-Маркова, Метод наименьших квадратов, приведённый к линейному преобразованию матриц или к системе линейных уравнений, обеспечивает наилучшую несмещенную, эффективную и сходящуюся к пределу (“состоятельную”) оценку вектора параметров, т.е. наилучшее качество линейной модели, если соблюдаются условия (по [ 1 ]):
GQ = e12/e22 где e12 и e22 – суммы квадратов остатков (отклонений) в первой и последней трети (или в половинах) диапазона Х; большая сумма делится на меньшую!!!; GQ сравнивают с критерием Фишера для заданных уровня значимости и количества измерений; гипотеза о гомоскедастичности принимается при GQ <4,35. 6. Отсутствие автокорреляции, т.е. взаимозависимости возмущений. Её оценивают, вычисляя статистику Дарбина-Уотсона остатков е: 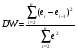 для которой вычислены критические значения при различных уровнях значимости и числе измерений. Приблизительно DW=0…1 означает положительную автокорреляцию, 3…4 отрицательную автокорреляцию, DW=1,5…2,5 позволяет принять гипотезу об отсутствии автокорреляции, DW=1…1,5 и DW=2,5…3 не позволяют принять гипотезу о наличии или отсутствии автокорреляции. Наличие автокорреляции означает, что аппроксимирующая функция подобрана неверно, или же требуется применение других методов и моделей. Автокорреляция разобрана в главе 8. Статистику Дарбина-Уотсона можно вычислить по формуле DW = 2(1-Rавт), где Rавт - коффициент автокорреляции, вычисляемый с помощью функции КОРРЕЛ: задать в окне Массив1 диапазон остатков с номерами 1 : n-1, а в окне Массив2 диапазон 2 : n. Понятия “гетероскедастичность” и “автокорреляция” актуальны, если массивы данных упорядочены, что имеет место для временных рядов. “Пространственные” данные можно искусственно упорядочить, например, отсортировав их по возрастанию какой-либо переменной; при этом можно выявить кластеры с аномальной дисперсией остатков, что может означать неоднородность выборки или неадекватность модели. Считается, что гетероскедастичность может привести к снижению эффективности оценок коэффициентов, и надо её искусственно подавлять: делить остатки в таблице 3.3 на их стандартные отклонения в диапазонах, а затем минимизировать сумму их квадратов. Эта технология называется Взвешенный метод наименьших квадратов (ВМНК) и обычно используется в матричном варианте МНК (раздел 3.3). При обнаружении автокорреляции остатков применяется Обобщённый метод наименьших квадратов ОМНК, основанный на преобразовании матриц, но с учётом корреляций остатков. Есть положительная автокорреляция, где за положительным отклонением следует положительное, за отрицательным – отрицательное. Отрицательная автокорреляция - за положительным чаще всего следует отрицательное. Автокорреляция чаще всего появляется в моделях временных рядов и моделировании циклических процессов Причина – неправильный выбор спецификации модели. ^ Последствия автокорреляции - оценки коэффициентов теряют эффективность; - стандартные ошибки коэффициентов занижены Типы автокорреляции Авторегрессия 1-го порядка: AR(1) Авторегрессия 5-го порядка: AR(5) Автокорреляция скользящих средних 3-го порядка: 13.Алгоритм проверки значимости регрессора в парной регрессионной модели. При проверке качества спецификации парной регрессии наиболее важной является задача установления наличия линейной зависимости между эндогенной переменной и регрессором модели. С этой целью проверяют значимость оценки параметра b (при регрессоре модели). Алгоритм проверки значимости параметра b выполняется в следующей последовательности: 1) оценка параметров парной регрессии 2) оценка дисперсии возмущений S2 3) оценка 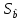 среднего квадратичного отклонения параметра b среднего квадратичного отклонения параметра b4) выбор значения tкр (по заданному уровню значимости 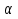 и числу степеней свободы (n-2) из таблиц распределения Стьюдента) и числу степеней свободы (n-2) из таблиц распределения Стьюдента)5) проверка неравенства 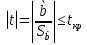 при Н0: b=0 при Н0: b=0Если данное неравенство выполняется, то регрессор признается незначимым, если не выполняется, то данная гипотеза отвергается и регрессор признается значимым, т.е. между эндогенной переменной и регрессором присутствует линейная зависимость. 14.Интервальная оценка ожидаемого значения зависимой переменной в парной регрессионной модели. Эконометрические модели предназначены для объяснения (прогноза) текущих значений зависимой переменной по заданным (наблюдаемым) значениям предопределенных (независимых) переменных. Например, модель линейной парной регрессии 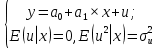 создаетсядля прогноза значений зависимой (эндогенной) переменной y по заданным (наблюдаемым) значениям экзогенной переменной х (регрессора модели). Прогнозировать значения переменной можно лишь тогда, когда модель признана адекватной. Для проверки адекватности модели линейной парной регрессии рассчитываем нормированную ошибку прогноза по формуле создаетсядля прогноза значений зависимой (эндогенной) переменной y по заданным (наблюдаемым) значениям экзогенной переменной х (регрессора модели). Прогнозировать значения переменной можно лишь тогда, когда модель признана адекватной. Для проверки адекватности модели линейной парной регрессии рассчитываем нормированную ошибку прогноза по формуле 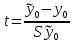 , где , где 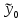 – прогноз, – прогноз,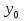 - наблюдаемое в реальности значение переменной, - наблюдаемое в реальности значение переменной, 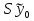 - средняя квадратическая ошибка прогноза. - средняя квадратическая ошибка прогноза.При этом если случайный остаток в рассматриваемой модели не имеет автокорреляции и нормально распределен, то tподчиняется закону распределения Стьюдента с числом степеней свободы 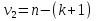 , где k+1 – количество оцениваемых коэффициентов модели (для модели линейной парной регрессииk+1=2).Данное обстоятельство позволяет построить замкнутый интервал , где k+1 – количество оцениваемых коэффициентов модели (для модели линейной парной регрессииk+1=2).Данное обстоятельство позволяет построить замкнутый интервал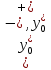 с границами с границами 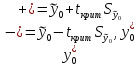 , именуемый доверительным интервалом, который включает прогнозируемые значения , именуемый доверительным интервалом, который включает прогнозируемые значения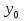 с принятой доверительной вероятностью с принятой доверительной вероятностью 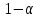 . .В случае парной регрессии можно оценить интервальное среднеквадратичное отклонение Yпрогноз по формуле 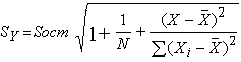 и посмотреть, попадают ли реальные значения Y в интервал Ŷ 2SYпрогноз. 15. Тест Чоу на наличие структурных изменений в регрессионной модели. (20) стр. 59,60 Тест Чоу позволяет количественно оценить выгоду от усложнения модели, например, замены одной прямой линии двумя или кривой. Результаты расчета по формуле Чоу сравнивается с критическими значениями статистики Фишера, что даёт основание принять или отвергнуть гипотезу об улучшении модели. 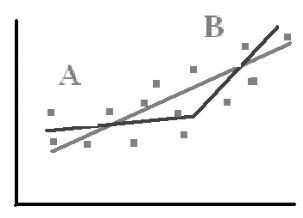 Рассмотрим диаграмму рассеяния на рисунке. Какую регрессионную модель использовать? Стоит ли заменять прямую линию на ломаную? Согласно тесту Чоу УЛУЧШЕНИЕ / Доп.Степени Свободы F(k, n-2k) = ------------------------------------------------------------------ Остаточное Σост2 /Остаточное число степеней свободыили ( Σост2 все – Σост2 А – Σост2B ) /k F(k, n-2k) = ---------------------------------------------------------- (Σост2 А + Σост2B ) / (n – 2k) 16. Алгоритм проверки адекватности парной регрессионной модели. (20) стр. 37, 79 Проверка модели на адекватность осуществляется следующим образом. Ряд измерений не используются при настройке модели, затем проводится прогноз соответствующих эндогенных переменных и сравнение прогнозных и реальных значений. В случае парной регрессии можно оценить интервальное среднеквадратичное отклонение Yпрогноз по формуле 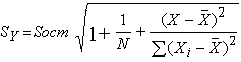 и посмотреть, попадают ли реальные значения Y в интервал Ŷ2SYпрогноз. В случае множественной регрессии, особенно при наличии мультиколлинеарности, оценить SYпрогноз достаточно сложно, и лучше сравнивать графики Y и Ŷ . 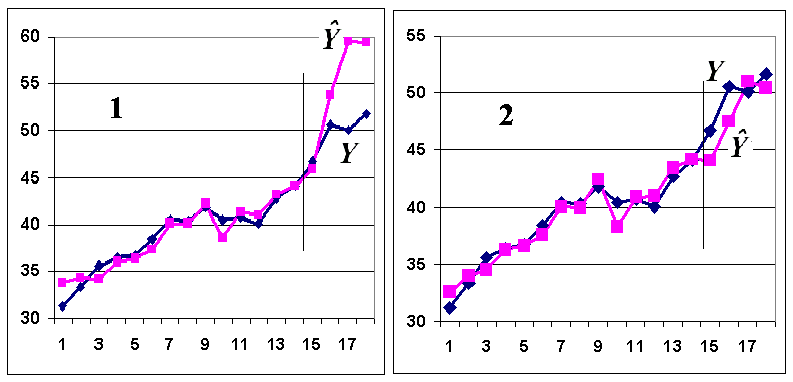 Рис.7.5. Проверка на адекватность аддитивной ( 1 ) и мультипликативной модели ( 2 ). 17. Коэффициент детерминации в парной регрессионной модели. Коэффициент детерминации (R2)— это доля дисперсии отклонений зависимой переменной от её среднего значения, объясняемая рассматриваемой моделью связи. Модель связи обычно задается как явная функция от объясняющих переменных. 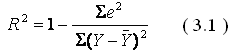 Коэффициент детерминации является случайной переменной. Он характеризует долю результативного признака у, объясняемую регрессией, в общей дисперсии результативного признака:  0≤ R2≤1. причем если R2= 1 то переменная yt полностью объясняется регрессором xt. В множественной регрессионной модели добавление дополнительных регрессоров увеличивает значение коэффициента детерминации, поэтому его корректируют с учетом числа независимых переменных: 0≤ R2≤1. причем если R2= 1 то переменная yt полностью объясняется регрессором xt. В множественной регрессионной модели добавление дополнительных регрессоров увеличивает значение коэффициента детерминации, поэтому его корректируют с учетом числа независимых переменных: 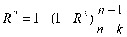 18. Оценка параметров множественной регрессионной модели методом наименьших квадратов. Парная регрессия характеризует связь между двумя признаками: результативным и факторным. Аналитическая связь между ними описывается уравнениями: Прямой - Проводят дифференцирование S по коэффицентам и приравнивают уравнения к 0. Из системы уравнений, получаем: 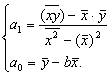 Здесь Здесь Значимость коэффициента регрессии осуществляется с помощью t-критерия Стьюдента (отношение коэффициента регрессии к его средней ошибке): . 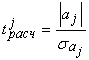 Коэффициент регрессии считается статистически значимым, если Коэффициент регрессии считается статистически значимым, если Проверка адекватности всей модели осуществляется с помощью F-критерия и величины средней ошибки аппроксимации Проверка адекватности всей модели осуществляется с помощью F-критерия и величины средней ошибки аппроксимации 19. F-тест качества спецификации парной регрессионной модели Оценка значимости уравнения регрессии в целом даётся с помощью F-критерия Фишера. При этом проверяется нулевая гипотеза, что коэффициент регрессии равен нулю и, следовательно, фактор X не оказывает влияния на результат Y. Статистика Фишера равна частному от деления дисперсии Ŷ, или факторной дисперсии, и дисперсии остатков, вычисленных с учётом числа степеней свободы: 1 для Ŷ и n-2 для остатков. Полезно помнить, что при уровне значимости =0,05, то есть при доверительной вероятности 95% и количестве замеров более 15 критическое значение F для парной регрессии около 4,2 , а при m=4 около 3. Начиная с этих значений F можно говорить о существовании влияния регрессоров на эндогенную переменную. Таблицы критических значений F есть во всех книгах по мат.статистике и эконометрике, поэтому в этой книге они не приводятся. Их можно вычислить в Excel с помощью функции FРАСПОБР с аргументами: уровень значимости (здесь =0,05); число регрессоров m; N-m-1; где Nчисло измерений. 20. Гетероскедастичность случайного возмущения. Причины. Последствия. Тест GQ(20) Равенство ожидаемых значений дисперсий возмущений в разных диапазонах Х: E(u2)= Const. Это свойство называется гомоскедастичность, его несоблюдние – гетероскедастичность. Отклонение от гомоскедастичности проверяется по тесту Голдфелда-Квандта GQ = e12/e22 где e12 и e22 – суммы квадратов остатков (отклонений) в первой и последней трети (или в половинах) диапазона Х; большая сумма делится на меньшую!!!; GQ сравнивают с критерием Фишера для заданных уровня значимости и количества измерений; гипотеза о гомоскедастичности принимается при GQ <4,35. Причина: При гетероскедастичности распределение u для каждого наблюдения имеет нормальное распределение и нулевое ожидание, но дисперсия распределений различна. Последствия нарушения условия гомоскедастичности случайных возмущений:1. Потеря эффективности оценок коэффициентов регрессии, т.е. можно найти другие, отличные от Метода Наименьших Квадратов и более эффективные оценки 2. Смещенность стандартных ошибок коэффициентов в связи с некорректностью процедур их оценки/ 21.Фиктивная переменная наклона: назначение; спецификация регрессионной модели с фиктивной переменной наклона; значение параметра при фиктивной переменной. (20) стр.65 Фиктивные (dummy) переменные позволяют ввести в модель и учесть качественные характеристики, например пол покупателей, расположение магазина и т.п. Например, задача может быть модифицирована Y = a + bX + cz + u или Y = a + b(1+cz)X +u, где переменная z принимает значения 0 или 1. Фиктивные переменные позволяют объединить в одной модели выборки, имеющие отличия. В принципе, их можно рассматривать отдельно, но объединение может дать более качественную модель. Повышение качества модели можно оценить, используя тест Чоу. В регрессионных моделях наряду с количественными переменными часто используются качественные переменные, которые выражаются в виде фиктивных (искусственных) переменных, отражающих два противоположных состояния качественного фактора. Например, D=0, если потребитель не имеет высшего образования, D=1, если потребитель имеет высшее образование. Переменная D называется фиктивной, или двоичной переменной, а также индикатором. Регрессионные модели, содержащие лишь качественные объясняющие переменные, называются ANOVA – моделями (моделями дисперсионного анализа). ANOVA – модели представляют собой кусочно – постоянные функции. Такие модели в экономике крайне редки. Гораздо чаще встречаются модели, содержащие как количественные, так и качественные переменные. Такие модели называются ANCOVA – моделями (моделями ковариационного анализа). В случае, когда качественная переменная принимает не два, а большее число значений, может возникнуть ситуация, которая называется ловушкой фиктивной переменной. Она возникает, когда для моделирования k значений качественного признака используется ровно k бинарных (фиктивных) переменных. В этом случае одна из таких переменных линейно выражается через все остальные, и матрица значений переменных становится вырожденной. Тогда исследователь попадает в ситуацию совершенной мультиколлинеарности. Избежать подобной ловушки позволяет правило: - если качественная переменная имеет k альтернативных значений, то при моделировании используется только (k-1) фиктивных переменных. Нулевой уровень качественной переменной называется базовым или сравнительным. Кроме того, значения фиктивных переменных можно изменять на противоположные. Суть модели от этого не изменится. Изменится только знак коэффициентаg в модели. Коэффициент g в модели называется дифференциальным свободным членом, т.к. он показывает, на какую величину изменится свободный член модели при изменении значения фиктивной переменной. Возможны модели, в которых используются несколько фиктивных переменных, не связанных между собой по смыслу. Тогда возможны все комбинации значений различных качественных переменных, в которых регрессии отличаются лишь свободными членами. Подобные схемы можно распространить на произвольное число количественных или качественных факторов. При этом не следует забывать, что если качественный фактор имеет k альтернативных состояний, то для его описания можно использовать только k различных сочетаний значений (k-1) фиктивных переменных. Влияние качественного фактора может сказываться не только на значении свободного члена, но и на угловом коэффициенте линейной регрессионной модели. Обычно это характерно для временных рядов экономических данных при изменении институциональных условий, введении новых правовых или налоговых ограничений. Тогда зависимость может быть выражена так: где 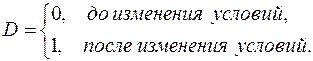 В этой ситуации ожидаемое значение зависимой переменной определяется следующим образом:  Коэффициенты g1 и g2 называются соответственно дифференциальным свободным членом и дифференциальным угловым коэффициентом. Фиктивная переменная разбивает зависимость на две части – до и после внесения изменений в условия её действия. Общая зависимость имеет вид кусочно – линейной функции, а изменения условий отображаются изменением угла наклона прямой к оси абсцисс. Здесь исследователь должен принять решение, стоит ли разбивать выборку на части и строить для каждой из них уравнение регрессии или ограничиться одной общей линией регрессии. Для этого используют тест Чоу, который состоит в следующем. Вся выборка объёма n разбивается на две подвыборки объёмами n1 и n2 (n1+n2=n), и для каждой строится уравнение регрессии. Кроме того, строится общая регрессия для всех наблюдений, и для неё определяется остаточная СКО. Равенство возможно лишь при совпадении коэффициентов регрессии для всех трёх уравнений. Если сумма будет значительно меньше, то можно считать разбиение общей выборки на две подвыборки обоснованным. В этом смысле разность можно считать мерой улучшения качества модели при разбиении выборки на две части. Однако при разбиении уменьшается число степеней свободы каждой из подвыборок. Эта альтернатива между числом степеней свободы и уменьшением остаточной СКО выражается через статистику. 22..Алгоритм теста Дарбина-Уотсона на наличие (отсутствие) автокорреляции случайных возмущений. (20) стр 33 Отсутствие автокорреляции, т.е. взаимозависимости возмущений. Её оценивают, вычисляя статистику Дарбина-Уотсона остатков е:  для которой вычислены критические значения при различных уровнях значимости и числе измерений. Приблизительно DW=0…1 означает положительную автокорреляцию, 3…4 отрицательную автокорреляцию, DW=1,5…2,5 позволяет принять гипотезу об отсутствии автокорреляции, DW=1…1,5 и DW=2,5…3 не позволяют принять гипотезу о наличии или отсутствии автокорреляции. Наличие автокорреляции означает, что аппроксимирующая функция подобрана неверно, или же требуется применение других методов и моделей. Статистику Дарбина-Уотсона можно вычислить по формуле DW = 2(1-Rавт), где Rавт - коффициент автокорреляции, вычисляемый с помощью функции КОРРЕЛ: задать в окне Массив1 диапазон остатков с номерами 1 : n-1, а в окне Массив2 диапазон 2 : n. 23. Структурная и приведённая формы спецификации эконометрических моделей. Система совместных, одновременных уравнений (или структурная форма модели) обычно содержит эндогенные и экзогенные переменные. Эндогенные переменные – это зависимые переменные, число которых равно числу уравнений в системе и которые обозначаются через Экзогенные переменные – это предопределенные переменные, влияющие на эндогенные переменные, но не зависящие от них, независимые переменные, которые определяются вне системы. Обозначаются через В качестве экзогенных переменных могут рассматриваться значения эндогенных переменных за предшествующий период времени (лаговые переменные). Предопределенными переменными наз. экзогенные и лаговые эндогенные переменные системы. Структурная форма модели позволяет увидеть влияние изменений любой экзогенной переменной на значения эндогенной переменной. Структурная форма модели в правой части содержит при эндогенных переменных коэффициенты  Использование МНК для оценивания структурных коэффициентов модели дает, как принято считать в теории, смещенные и несостоятельные оценки. Поэтому обычно для определения структурных коэффициентов модели структурная форма модели преобразуется в приведенную форму модели. Приведенная форма модели представляет собой систему линейных функций эндогенных переменных от экзогенных:  (3.4) (3.4)где По своему виду приведенная форма модели ничем не отличается от системы независимых уравнений, параметры которой оцениваются традиционным МНК. Применяя МНК, можно оценить Коэффициенты приведенной формы модели представляют собой нелинейные функции коэффициентов структурной формы модели. Структурные модели можно подразделить на три вида: - идентифицируемые;-неидентифиц.;- сверхидентифицируемые. Условие идентифицируемости модели может быть записано в виде следующего правила: Предопределённых + 1 = Эндогенных идентифицируемо Предопределённых + 1 < Эндогенных неидентифицируемо Предопределённых + 1 > Эндогенных сверхидентифицируемо 24. Гетероскедастичность случайного возмущения. Причины. Последствия. Алгоритм теста Голдфельда-Квандта на наличие или отсутствие гетероскедастичности случайных возмущений. Гетероскедастичность - ситуация, когда дисперсия ошибки в уравнении регрессии изменяется от наблюдения к наблюдению. В этом случае приходится подвергать определенной модификации МНК (иначе возможны ошибочные выводы). Для обнаружения гетероскедастичности обычно используют 3 теста: тест ранговой корреляции Спирмена, тест Голдфеда - Квандта и тест Глейзера Доугерти. Гетероскедастичность случайных возмущений – возмущения обладают различными дисперсиями r2i=r2wi, но не коррелированны друг с другом. Причина: При гетероскедастичности распределение u для каждого наблюдения имеет нормальное распределение и нулевое ожидание, но дисперсия распределений различна. Последствия нарушения условия гомоскедастичности случайных возмущений: 1. Потеря эффективности оценок коэффициентов регрессии, т.е. можно найти другие, отличные от Метода Наименьших Квадратов и более эффективные оценки 2. Смещенность стандартных ошибок коэффициентов в связи с некорректностью процедур их оценки ипотеза(1): |
