1. Метод наименьших квадратов алгоритм метода условия применения
 Скачать 281.01 Kb. Скачать 281.01 Kb.
|
|
Векторная авторегрессия (VAR, Vector AutoRegression)- модель динамики нескольких временных рядов, в которой текущие значения этих рядов зависят от прошлых значений этих же временных рядов. Модель предложена Кристофером Симзом как альтернатива системам одновременных уравнений, которые предполагают существенные теоретические ограничения. VAR-модели свободны от ограничений структурных моделей. Тем не менее, проблема VAR-моделей заключается в резком росте количества параметров с увеличением количества анализируемых временных рядов и количества лагов. Используя этот метод, профессор Кристофер Симз получил в 2012 году Нобелевскую премию за изучение влияния на экономику эффектов от единовременных потрясений и действий регуляторов, в частности, изменения процентных ставок центробанков. Согласно его модели, негативные эффекты от повышения ставок (снижение экономической активности) проявляются почти сразу же, тогда как положительных результатов, например сокращения инфляции, приходится ждать порой несколько лет. Вместе с ним Нобелевскую премию получил Томас Сарджент, который наблюдал за реакцией банков, компаний и индивидов при повышении и понижении инфляции. Базируясь на этих исследованиях, Томас Сарджент сформулировал теорию, согласно которой на действия людей влияют не шаги правительства как таковые, а их ожидание. В результате эффект от той или иной стратегии может оказаться не совсем таким, какого ожидали власти. На этих же принципах основана рефлексивная модель Джорджа Сороса: поведение людей, в том числе биржевых игроков, зависит от подаваемой им информации. Управляя потоками информации, можно управлять и “толпой” биржевых игроков, а значит и ценами на бирже. 33.Идентифицируемость системы. Интерес представляют коэффициенты не приведённой модели, а структурной, которая имеет экономический смысл. Поэтому после настройки по статистическим данным приведённой модели и оценки её коэффициентов требуется вычислить по ним структурные коэффициенты. Но это не всегда получается: возникает проблема идентификации – единственности соответствия между приведённой и структурной формами модели. Структурные модели можно подразделить на три вида: - идентифицируемые; - неидентифицируемые; - сверхидентифицируемые. Модель идентифицируема, если структурные коэффициенты определяются однозначно, единственным образом по коэффициентам приведённой формы модели, то есть число параметров структурной модели равно числу параметров приведённой формы модели. Модель неидентифицируема, если число приведённых коэффициентов меньше числа структурных коэффициентов, и структурные коэффициенты не могут быть оценены через коэффициенты приведённой формы модели. Модель сверхидентифицируема, если число приведённых коэффициентов больше числа структурных коэффициентов. В этом случае на основе коэффициентов приведённой формы можно получить несколько значений каждого структурного коэффициента, число структурных коэффициентов меньше числа коэффициентов приведённой формы. Модель может быть практически решена при применении специальных методов. Структурная модель всегда представляет собой систему совместных уравнений, каждое из которых необходимо проверять на идентификацию. Модель считается идентифицируемой, если каждое уравнение системы идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель считается неидентифицируемой. Сверхидентифицируемая модель содержит хотя бы одно сверхидентифицируемое уравнение. Чтобы уравнение было идентифицируемо, нужно, чтобы число предопределённых переменных, отсутствующих в данном уравнении, но присутствующих в системе, было равно числу эндогенных переменных в данном уравнении без одного. Условие идентифицируемости модели может быть записано в виде следующего правила: Предопределённых + 1 = Эндогенных идентифицируемо Предопределённых + 1 < Эндогенных неидентифицируемо Предопределённых + 1 > Эндогенных сверхидентифицируемо Если обозначить число эндогенных переменных в j-м уравнении системы через Н, а число предопределённых переменных, которые содержатся в системе, но не входят в данное уравнение, через D, то D + 1 = Hидентифицируемо D + 1 < Hнеидентифицируемо D + 1 > Hсверхидентифицируемо В исследуемой модели d, p, s эндогенные; x, p(t-1) предопределённые, во всей системе их 2. Исследуем модель: Предопр.DD+1 Н d = a0 + a1· p + a2· x 1 1 2 2 идент. s = b0 + b1 · p(t-1) 1 1 2 1 сверх. d = s 0 2 2 2 идент. Значит, модель сверхидентифицируема. Идентифицируемую систему эконометрических уравнений можно решить Косвенным методом наименьших квадратов (КМНК). Суть метода в следующем: - Преобразование структурной формы модели в приведённую; - Оценка коэффициентов уравнений приведённой формы обычным методом наименьших квадратов; - Преобразовать их в коэффициенты структурной модели. Если при вычислении коэффициентов структурной формы (9.1) учитывать возмущения, то они войдут в оба уравнения модели, и принцип независимости эндогенных переменных и остатков будет нарушен. Это приведёт к смещению (отсутствию состоятельности) параметров модели. Для подавления этого эффекта, а также для настройки сверхидентифицируемых моделей используется двухшаговый метод наименьших квадратов ДМНК. Основная идея ДМНК – на основе приведённой формы модели получить для сверхидентифицируемого уравнения оценённые значения эндогенных переменных, содержащихся в правой части уравнения. Далее, подставив их в правые части уравнений вместо фактических значений, можно применить обычный МНК к структурной форме сверхидентифицируемого уравнения. Метод получил название “двухшаговый метод наименьших квадратов”, ибо МНК используется дважды: на первом шаге при определении коэффициентов приведённой формы модели и нахождении на её основе оценок оценённых значений эндогенных переменных Ŷ и на втором шаге применительно к структурному сверхидентифицируемому уравнению при определении структурных коэффициентов модели с использованием оценённых значений эндогенных переменных. Оценённые значения играют роль так называемых инструментальных переменных (instrumentalvariables, IV, instruments) – переменных, которые применяются, если обычные переменные коррелируют с возмущениями. Инструментальные переменные коррелируют с обычными переменными, но не коррелируют с возмущениями, что приводит к состоятельности (consistency) модели. Расчёты с использованием инструментальных переменных включены в статистические пакеты, так что не удивляйтесь, увидев IV на распечатке. Алгоритмы и краткие замечания по КМНК и ДМНК: Косвенный МНК: 1) Структурная => Приведенная 2) Коэффициенты по МНК 3) Преобразовать их в коэффициенты структурной модели Нарушение предпосылки независимости факторов приводит к несостоятельности оценок структурных коэффициентов, они могут оказаться бессмысленными Двухшаговый МНК Применяется для сверхидентифицируемых систем уравнений 1) Структурная => Приведенная. 2) Коэффициенты по МНК. 3) Получить оценённые значения эндогенных переменных. 4) Подставить их в правые части структурной формы. 5) Применить МНК к структурной форме сверхидентифицируемых уравнений. Сверхидентифицируемую модель можно превратить в идентифицируемую путем добавления некоторых переменных или отбрасывания некоторых ограничений на параметры 34. Настройка модели с системой одновременных уравнений. Наибольшее распространение в эконометрических исследованиях получила система взаимозависимых уравнений. В ней одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других уравнениях - в правую часть системы: y1 = b12* y2 + b13* y3 +… + b1n * yn + a11 * x1 + a12 * x2 +…+ a1m xm + e1, y2 = b21* y1 + b23* y3 +… + b2n * yn + a21 * x1 + a22 * x2 +…+ a2m xm + e2, yn = bn1* y1 + bn2* y2 +… + bnn-1 * yn-1 + an1 * x1 + an2 * x2 +…+ anm xm + en, Система взаимозависимых уравнений получила название система совместных, одновременных уравнений. Тем самым подчеркивается, что в системе одни и те же переменные одновременно рассматриваются как зависимые в одних уравнениях и как независимые в других. Экономические модели, значения переменных которых привязаны к моменту времени, называются динамическими. Примером системы одновременных уравнений может служить модель спроса и предложения, включающая три уравнения. В эконометрике эта система уравнений называется также структурной формой модели. В отличие от предыдущих систем каждое уравнение системы одновременных уравнений не может рассм. самостоятельно, и для нахождения его параметров традиционный МНК неприменим. С этой целью используются специальные приемы оценивания . Система совместных, одновременных уравнений (или структурная форма модели) обычно содержит эндогенные и экзогенные переменные. Эндогенные переменные - это зависимые переменные, число которых равно числу уравнений в системе и которые обозначаются через y. Экзогенные переменные - это предопределенные переменные, влияющие на эндогенные переменные, но не зависящие от них. Обозначаются через x. Классификация переменных на эндогенные и экзогенные зависит от теоретической концепции принятой модели. Эк. переменные могут выступать в одних моделях как эндогенные, а в других как экзогенные переменные. Внеэк. переменные (напр., климатич. условия, соц. положение, пол, возрастная категория) входят в систему только как экзогенные переменные. В качестве экзогенных переменных могут рассм. значения эндогенных переменных за предшествующий период времени (лаговые переменные). Целесообразно в качестве экзогенных переменных выбирать такие переменные, которые могут быть объектом регулирования. Меняя их и управляя ими, можно заранее иметь целевые значения эндогенных переменных. Примером системы одновременных уравнений может служить модель спроса и предложения, включающая три уравнения. 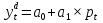 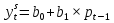 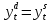 a1<0, b1>0 Второй пример:  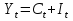 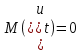 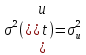 35.Что такое метод Монте-Карло стр 53 При работе на компьютере проще многократно проделать простые вычисления, чем один раз решить сложную аналитическую задачу. Поэтому для исследования стохастических моделей удобен метод Монте-Карло, позволяющий, в частности, оценивать погрешности параметров сложных моделей. Основные этапы реализации метода Монте-Карло: 1. Построение модели с “идеальными” параметрами. 2. Изменение значений переменных случайным образом в соответствии с дисперсией и законом распределения. 3. Расчет по проверяемой методике и сохранение параметров модели. 4. Возврат к п.2. Пункты 2 и 3 выполняются заданное число раз – десятки, сотни, тысячи. В результате накапливаются массивы параметров, которые можно статистически обработать и установить надежность их оценок. В принципе, это можно сделать по аналитическим формулам дисперсионного анализа, но для сложной системы с внутренними связями такие расчеты становятся сложными и неустойчивыми. 36.Оценить качество модели по F, GQ, DW (линейнные).стр.33, 28-29 Статистику Фишера удобно вычислять через коэффициент детерминации:
Чем больше статистика Фишера, тем лучше прогнозы, сделанные с использованием модели. Из формулы (3.3) следует, что F возрастает с ростом R2 и числа измерений, но уменьшается при увеличении числа влияющих переменных, то есть надо аккуратно подходить к включению в модель новых влияющих переменных, а также не использовать для аппроксимации полиномы высоких степеней. Полезно помнить, что при уровне значимости =0,05, то есть при доверительной вероятности 95% и количестве замеров более 15 критическое значение F для парной регрессии около 4,2 , а при m=4 около 3. Начиная с этих значений F можно говорить о существовании влияния регрессоров на эндогенную переменную. Таблицы критических значений F есть во всех книгах по мат.статистике и эконометрике, поэтому в этой книге они не приводятся. Их можно вычислить в Excel с помощью функции FРАСПОБР с аргументами: уровень значимости (здесь =0,05); число регрессоров m; N-m-1; где Nчисло измерений. Согласно теореме Гаусса-Маркова, Метод наименьших квадратов, приведённый к линейному преобразованию матриц или к системе линейных уравнений, обеспечивает наилучшую несмещенную, эффективную и сходящуюся к пределу (“состоятельную”) оценку вектора параметров, т.е. наилучшее качество линейной модели, если соблюдаются условия (по [ 1 ]):
5. Равенство ожидаемых значений дисперсий возмущений в разных диапазонах Х: E(u2)= Const. Это свойство называется гомоскедастичность, его несоблюдние – гетероскедастичность. Отклонение от гомоскедастичности проверяется по тесту Голдфелда-Квандта GQ = e12/e22 где e12 и e22 – суммы квадратов остатков (отклонений) в первой и последней трети (или в половинах) диапазона Х; большая сумма делится на меньшую!!!; GQ сравнивают с критерием Фишера для заданных уровня значимости и количества измерений; гипотеза о гомоскедастичности принимается при GQ <4,35. 6. Отсутствие автокорреляции, т.е. взаимозависимости возмущений. Её оценивают, вычисляя статистику Дарбина-Уотсона остатков е: 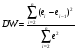 для которой вычислены критические значения при различных уровнях значимости и числе измерений. Приблизительно DW=0…1 означает положительную автокорреляцию, 3…4 отрицательную автокорреляцию, DW=1,5…2,5 позволяет принять гипотезу об отсутствии автокорреляции, DW=1…1,5 и DW=2,5…3 не позволяют принять гипотезу о наличии или отсутствии автокорреляции. Наличие автокорреляции означает, что аппроксимирующая функция подобрана неверно, или же требуется применение других методов и моделей. Автокорреляция разобрана в главе 8. Статистику Дарбина-Уотсона можно вычислить по формуле DW = 2(1-Rавт), где Rавт - коффициент автокорреляции, вычисляемый с помощью функции КОРРЕЛ: задать в окне Массив1 диапазон остатков с номерами 1 : n-1, а в окне Массив2 диапазон 2 : n. Понятия “гетероскедастичность” и “автокорреляция” актуальны, если массивы данных упорядочены, что имеет место для временных рядов. “Пространственные” данные можно искусственно упорядочить, например, отсортировав их по возрастанию какой-либо переменной; при этом можно выявить кластеры с аномальной дисперсией остатков, что может означать неоднородность выборки или неадекватность модели. Считается, что гетероскедастичность может привести к снижению эффективности оценок коэффициентов, и надо её искусственно подавлять: делить остатки в таблице 3.3 на их стандартные отклонения в диапазонах, а затем минимизировать сумму их квадратов. Эта технология называется Взвешенный метод наименьших квадратов (ВМНК) и обычно используется в матричном варианте МНК (раздел 3.3). При обнаружении автокорреляции остатков применяется Обобщённый метод наименьших квадратов ОМНК, основанный на преобразовании матриц, но с учётом корреляций остатков. 37. Оценка погрешностей параметров эконометрической модели методом Монте-Карло . При работе на компьютере проще многократно проделать простые вычисления, чем один раз решить сложную аналитическую задачу. Поэтому для исследования стохастических моделей удобен метод Монте-Карло, позволяющий, в частности, оценивать погрешности параметров сложных моделей. Основные этапы реализации метода Монте-Карло: 1. Построение модели с “идеальными” параметрами. 2. Изменение значений переменных случайным образом в соответствии с дисперсией и законом распределения. 3.Расчет по проверяемой методике и сохранение параметров модели. 4. Возврат к п.2. Пункты 2 и 3 выполняются заданное число раз – десятки, сотни, тысячи. В результате накапливаются массивы параметров, которые можно статистически обработать и установить надежность их оценок. В принципе, это можно сделать по аналитическим формулам дисперсионного анализа, но для сложной системы с внутренними связями такие расчеты становятся сложными и неустойчивыми. 38. Отражение в модели влияния неучтённых факторов. Предпосылки теоремы Гаусса-Маркова. Согласно теореме Гаусса-Маркова, Метод наименьших квадратов, приведённый к линейному преобразованию матриц или к системе линейных уравнений, обеспечивает наилучшую несмещенную, эффективную и сходящуюся к пределу (“состоятельную”) оценку вектора параметров, т.е. наилучшее качество линейной модели, если соблюдаются условия (по [ 1 ]): 1. Линейная модель соответствует действительности. 2. Существует дисперсия регрессора. 3. Математическое ожидание возмущения равно нулю: E(ui) = 0. 4. Возмущение имеет нормальное распределение. 5. Равенство ожидаемых значений дисперсий возмущений в разных диапазонах Х: E(u2) = Const. Это свойство называется гомоскедастичность, его несоблюдние – гетероскедастичность. Отклонение от гомоскедастичности проверяется по тесту Голдфелда-Квандта GQ = e12/e22 где e12 и e22 – суммы квадратов остатков (отклонений) в первой и последней трети (или в половинах) диапазона Х; большая сумма делится на меньшую!!!; GQ сравнивают с критерием Фишера для заданных уровня значимости и количества измерений; гипотеза о гомоскедастичности принимается при GQ <4,35. 6. Отсутствие автокорреляции, т.е. взаимозависимости возмущений. Её оценивают, вычисляя статистику Дарбина-Уотсона остатков е: 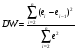 для которой вычислены критические значения при различных уровнях значимости и числе измерений. Приблизительно DW=0…1 означает положительную автокорреляцию, 3…4 отрицательную автокорреляцию, DW=1,5…2,5 позволяет принять гипотезу об отсутствии автокорреляции, DW=1…1,5 и DW=2,5…3 не позволяют принять гипотезу о наличии или отсутствии автокорреляции. Наличие автокорреляции означает, что аппроксимирующая функция подобрана неверно, или же требуется применение других методов и моделей. 39.Модели временных рядов. Свойства рядов цен акций на бирже (20) с.93. Временной ряд – это датированная целочисленными моментами времени t экономическая переменная. Эта переменная служит количественной характеристикой некоторого экономического объекта, поэтому изменение этой переменной во времени определяется факторами, оказывающими воздействие на данный объект с ходом времени. Все факторы делятся на 3 класса. 1 класс: факторы («вековые» воздействия), результирующее влияние которых на данный объект на протяжении длительного отрезка времени не изменяют своего направления. Они порождают монотонную составляющую (тенденцию или тренд). 2 класс: факторы (циклические воздействия), результирующее влияние которых на объект совершает законченный круг в течение некоторого фиксированного промежутка времени T. 3 класс: факторы (случайные воздействия),результирующее влияние которых на объект с высокой скоростью меняет направление и интенсивность. 3 Класс факторов позволяют интерпретировать величину в каждый период времени как случайную переменную Модели AR и VAR Авторегрессионная (AR-) модель (англ. Autoregressive model) — модель временных рядов, в которой значения временного ряда в данный момент линейно зависят от предыдущих значений этого же ряда. Авторегрессионный процесс порядка p (AR(p)-процесс)- определяется следующим образом Xt=c+∑i=1paiXt−i+εt, где a1,…,ap — параметры модели (коэффициенты авторегрессии), c -постоянная (часто для упрощения предполагается равной нулю), а εt — белый шум. Векторная авторегрессия (VAR, Vector AutoRegression)- модель динамики нескольких временных рядов, в которой текущие значения этих рядов зависят от прошлых значений этих же временных рядов. Модель предложена Кристофером Симсом как альтернатива системам одновременных уравнений, которые предполагают существенные теоретические ограничения. VAR-модели свободны от ограничений структурных моделей. Тем не менее, проблема VAR-моделей заключается в резком росте количества параметров с увеличением количества анализируемых временных рядов и количества лагов. алгоритм прогнозирования цен на бирже: 1) отбросить ряды с резкими бросками цен; 2) вычесть из ряда тренды, используя средства Excel; 3) построить график остатков и оценить стационарность этого ряда; 4) построить коррелограмму по ряду остатков; 5) проанализировать вид коррелограммы; если первый ноль в районе 5-8 и второй 16-25, можно применить синусоидальную аппроксимацию; 6) если перед сегодняшним днем на графике цен или остатков видны 1,5 - 3 волны, целесообразно применить синусоидальную аппроксимацию: постройте для области настройки функцию Ŷ(t) = a + b t + d Sin(ωt+φ) (модифицированная модель Брауна) , где Ŷ(t)- значение аппроксимирующей функции t - время (день, час и др.) a, b, d, ω, φ – коэффициенты аппроксимирующей функции. Для оценки коэффициентов используется метод наименьших квадратов с применением сервиса Excel “Поиск решения”. Вначале коэффициенты задаются произвольно (“опорный план”) и проводится вычисление функции Ŷ(t) в разумном диапазоне значений цен и на прогнозируемый период времени. Под “разумным диапазоном” следует понимать временной диапазон, в котором не было резких скачков цен и изменений тренда, и можно увидеть 1,5 – 2 волны. Обычно это 30-50 точек независимо от Δt. Затем вычисляется сумма квадратов отклонений (Ŷ(t)-Цена)2, которая является целевой минимизируемой функцией изменяемых коэффициентов. Скорее всего, первая итерация даст плохой результат для коэффициента, и его надо изменять вручную, запуская затем “Поиск решения”. Это связано с тем, что временной ряд представляет собой суперпозицию непериодических колебаний, в которых можно найти широкий спектр частот, и компьютер находит частоту, ближайшую к исходному значению. В целом, метод позволяет угадывать движение цены до 10 периодов с вероятностью более 50 %, но фаза третьей, а тем более четвертой волны обычно сдвигается, что приводит к ошибочным прогнозам. 40. Ожидаемое значение случайной переменной, её дисперсия и среднее квадратическое отклонение. (20) с.12-21 Переменная величина х с областью изменения Х называется случайной, если в результате некоторого опыта со случайными элементарными исходами она принимает значение из множества Х, которое заранее невозможно предсказать. Случайная величина может быть дискретной или непрерывной. Важную роль играют две количественные харак теристики случайной переменной х: математическое ожидание (ожидаемое значение) и дисперсия. Ожидаемое зна чение, которое обычно обозначают , m или Е(х) находится по формуле 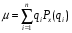 ( 2.1 ) ( 2.1 )Подчеркнем, что – это константа, вокруг которой рассеяны возможные значения qслучайной переменной х. Дисперсия 2, Var(x) – это математическое ожидание квадрата отклонения случайной переменной х от её ожидаемого значения: 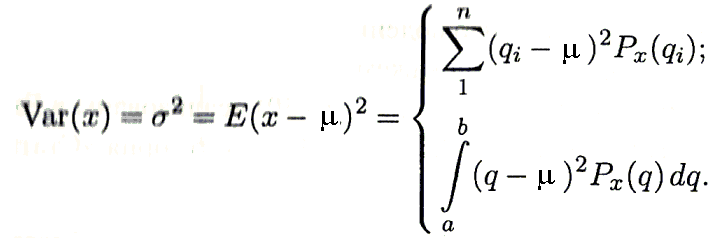 ( 2.2 ) Положительный квадратный корень из дисперсии 2 = Е(х2) - 2( 2.3 ) который часто используется для расчётов вручную. Из формул (2.1) - (2.2) видно, что для отыскания величин , нужно знать закон распределения Px(q) случайной пере менной х. Часто это закон неизвестен, и тогда можно оценить (приближенно определить) характеристики , 2по результатам n независимых наблюдений (опытов) { х1, х2, …, хn}. В этом наборе каждая компонента хi– это случайная пере менная с одним и тем же законом распределения Px(q), при этом величины хiявляются независимыми. Что такое наилучшая оценка, или наилучшая технология оценки (estimator) математического ожидания случайной величины? Каковы её критерии? 1. Несмещенность. Применяя правильную технологию расчёта, мы не получим в результате обработки серии замеров статистически значимого отклонения от реального значения оцениваемого параметра. 2. Эффективность. среднее значение обеспечивает наиболее эффективную оценку математического ожидания Е(х). Эффективность может вступить в противоречие с несмещённостью. Например, исключение переменных из эконометрических моделей может привести к уменьшению дисперсий оцениваемых параметров и к их смещению относительно истинных значений. 3. Consistency. В российских учебниках это слово переводят как “состоятельность”, но правильнее говорить о сходимости. Это значит, что увеличивая количество замеров в серии n, мы можем получить разность оценок исследуемого параметра меньше любого , то есть наши оценки сходятся к какому-то пределу. 41. Оценка параметров парной регрессионной модели методом наименьших квадратов с использованием сервиса Поиск решения. Парная регрессия характеризует связь между двумя признаками: результативным и факторным. Аналитическая связь между ними описывается уравнениями: Прямой - Проводят дифференцирование S по коэффицентам и приравнивают уравнения к 0. Из системы уравнений, получаем: Значимость коэффициента регрессии осуществляется с помощью t-критерия Стьюдента (отношение коэффициента регрессии к его средней ошибке): . Проверка адекватности всей модели осуществляется с помощью F-критерия и величины средней ошибки аппроксимации Проверка адекватности всей модели осуществляется с помощью F-критерия и величины средней ошибки аппроксимации Использование сервиса Поиск решения позволяет наглядно продемонстрировать суть метода наименьших квадратов (МНК). Вызывается он так же, как и Анализ данных: в Excel-2003 и более ранних версиях через меню Сервис (если не вызывается, то Сервис-Надстройки) ; в Excel-2007 и 2010 в меню Данные (если не вызывается, то Пуск – Параметры Excel – Надстройки – Перейти). Схема расчетов та же, что и в задачах математического программирования: задать произвольные коэффициенты аппроксимирующей функции f(X) , построить функцию Ŷ = f(X) в заданном диапазоне Х, вычислить отклонения Y – Ŷ для диапазона, в котором значения Y используются для настройки модели, то есть оценки коэффициентов, вычислить все (Y – Ŷ )2и их сумму (Y – Ŷ )2(сумма квадратов отклонений (остатков) , вызвать Поиск решения, целевая ячейка (Y – Ŷ)2, Изменяя ячейки коэффициенты, ограничений нет, Выполнить. Метод наименьших квадратов с Поиском решения может применяться для настройки нелинейных моделей. Показатель качества линейной модели – коэффициент корреляции Х и Y Rxy и его квадрат – коэффициент детерминации R2. Вычисленные для обеих моделей R2, DW, GQ представлены в таблицах, а также показаны графики остатков. Видно, что качество обеих моделей высокое, применение МНК правомерно. Применение для прогноза одной из двух моделей зависит от дополнительной информации и личного опыта. 42. Проверка статистических гипотез, t-статистика Стьюдента, доверительная вероятность и доверительный интервал, критические значения статистики Стьюдента. Что такое “толстые хвосты”? Инженеры считают, что размеры деталей подчиняются закону нормального распределения (ЗНР), выведенного К.Гауссом 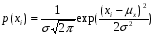 Как видите, в функции Гаусса всего два параметра: математическое ожидание µх и стандартное отклонение , которые сравнительно легко оценить по выборке, используя формулы (2.4) и (2.5 ). Эти формулы реализованы в Excel в функциях соответственно СРЗНАЧ, ДИСП и СТАНДОТКЛОН, категория «Статисти ческие». Зная параметры гауссианы, можно вычислить процент деталей в различных диапазонах х (квантили), используя таблицы или функцию НОРМРАСП Excel. Поэтому закон нормального распределения широко применяется при проектировании машин и механизмов. Например, можно вычислить количество событий (деталей) в диапазоне {Е(х) -2, Е(х) +2}. Это примерно 95%, то есть в “хвостах” останется по 2,5%. В данном случае р = 0,95 – доверительная вероятность, а {Е(х) -2, Е(х) +2} - соответствующий доверительный интервал. На Рисунке 2.2 показано применение функции НОРМРАСП. Площадь левого хвоста гауссианы (Рисунок 2.1) от - В общем виде это утверждение выглядит следующим образом: для уровня значимости = 1– р доверительный интервал равен {Е(х) – tкрит, Е(х) + tкрит}, где tкрит – критические значения статистики Стьюдента t = Е(х)/. В нашем примере – доля деталей в одном или двух “хвостах”. При уменьшении числа замеров надёжность оценки Е(х) и дисперсии падают, и доверительный интервал надо расширять. Поэтому критические значения статистики Стьюдента зависят от уровня значимости (доверительной вероятности) и количества замеров (степеней свободы). Распределение Стьюдента tкрит(, n) приведено во всех учебниках и практикумах по математической статистике и эконометрике. В Excel имеется функция СТЬЮДРАСП(tкрит, n, число хвостов (1 или 2)), которая возвращает долю событий в одном или двух “хвостах”. Для практических целей достаточно запомнить, что при числе замеров больше 30 и р=95% tкрит примерно равно 2 (при “бесконечном” числе замеров – 1,96). Для принятия гипотезы о влиянии регрессора на эндогенную переменную используются таблицы критических значений t-статистики Стьюдента. Для bt=b/Sb . Предполагается, что при числе измерений больше 20 истинные значения коэффициентов уравнения регрессии и лежат в интервалах {a-2Sa , b+2 Sb } и {b-2Sb , b+2 Sa } с доверительной вероятностью 95%. 43.Проблема мультиколлинеарности в моделях множественной регрессии. Признаки мультиколлинеарности Множественная регрессия позволяет построить и проверить модель линейной связи между зависимой (эндогенной) и несколькими независимыми (экзогенными) переменными: y = f(x1,...,xр ), где у - зависимая переменная (результативный признак); х1,...,хр - независимые переменные (факторы). Множественная линейная регрессионная модель имеет вид: y=a+b1x1+b2x2+…+bpxp+ε Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям: 1. быть количественно измеримы. При включении качественного фактора нужно придать ему количественную определенность 2. не должны быть коррелированы между собой и тем более и годиться в точной функциональной связи. Включение в модель факторов с высокой интеркорреляцией, когда ryx1 < rx1x2 может повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии. Поскольку одним из условий построения уравнения множественной регрессии является независимость действия факторов, коллинеарность факторов нарушает это условие. Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами Признаки мультиколлинеарности. 1.В модели с двумя переменными одним из признаков мультиколлинеарности является близкое к единице значение коэффициента парной корреляции. Если значение хотя бы одного из коэффициентов парной корреляции больше, чем 0,8, то мультиколлинеарность представляет собой серьезную проблему. Однако в модели с числом независимых переменных больше двух, парный коэффициент корреляции может принимать небольшое значение даже в случае наличия мультиколлинеарности. В этом случае лучше рассматривать частные коэффициенты корреляции. 2. Для проверки мультиколлинеарности можно рассмотреть детерминант матрицы коэффициентов парной корреляции |r|. Этот детерминант называется детерминантом корреляции |r| ∈(0; 1). Если |r| = 0, то существует полная мультиколлинеарность. Если |r|=1, то мультиколлинеарность отсутствует. Чем ближе |r| к нулю, тем более вероятно наличие мультиколлинеарности. 3. Если оценки имеют большие стандартные ошибки, невысокую значимость, но модель в целом значима (имеет высокий коэффициент детерминации), то это свидетельствует о наличие мультиколлинеарности. 4. Если введение в модель новой независимой переменной приводит к существенному изменению. 44. Частные коэффициенты детерминации. Частный коэффициент детерминации показывает, на сколько процентов вариация результативного признака объясняется вариацией первого признака, входящего в множественное уравнение регрессии. Проверка существенности частных коэффициентов детерминации играет важную роль при построении многофакторных регрессионных моделей. Определенный на основе теоретического анализа набор факторных признаков может содержать и такие признаки, которые в данной конкретной совокупности не оказывают существенного влияния на результативный признак. Коэффициенты регрессии при таких несущественных факторах бывают настолько искажены случайными воздействиями и ненадежны, что не имеют никакого реального смысла. К тому же сохранение в уравнении несущественных факторов лишь засоряет модель и может исказить параметры при других переменных и лишить их экономического смысла Частные коэффициенты детерминации, характеризуют тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включённых в уравнение регрессии. Расчётная формула частного коэффициента детерминации  где R2безXi – коэффициент детерминации, вычисленный при исключённом из модели факторе Xi. 45. Спецификация и оценивание МНК нелинейных эконометрических моделей. Довольно часто приходится использовать нелинейные функции регрессии двух видов: 1. Регрессии, нелинейные относительно включённых в анализ объясняющих переменных: Полином второй, редко третьей степени y = a + bx+сх2+u. Гипербола y = a +b/x +u. Эти модели сводятся к линейным заменой переменных: z = х2 для полинома и z=1/x для гиперболы. После этого можно использовать функцию ЛИНЕЙН и сервис Регрессия, выделяя в качестве влияющих переменных х и z для полинома и z для гиперболы. 2. Регрессии, нелинейные по оцениваемым параметрам относятся: Степенная y = axb; Показательная y = abx; Экспоненциальная y = ea+bx. Здесь =1+ u. Эти модели могут быть линеаризованы логарифмированием, после чего можно использовать функцию ЛИНЕЙН и сервис Регрессия. Например, показательная функция преобразуется в ln(y) =ln(a) +xln(b)+ln(), или, после переименования z=A+cx+v. После нахождения коэффициентов A и c можно вычислить z^=A+cxиy^=exp(z^). 46. Экономический смысл коэффициентов линейного и степенного уравнений регрессии. Для линейного – маржинальная функция (производная) для степенного – эластичность. Линейное уравнение регрессии имеет вид y = a +bx + e, Коэффициенты b и a можно вычислить по формулам Коэффициент b показывает среднее изменение результативного показателя (в единицах измерения у) с повышением или понижением величины фактора х на единицу его измерения. Коэффициент a формально показывает прогнозируемый уровень у, но только в том случае, если х=0 находится близко с выборочными значениями. Но если х=0 находится далеко от выборочных значений х, то буквальная интерпретация может привести к неверным результатам, и даже если линия регрессии довольно точно описывает значения наблюдаемой выборки, нет гарантий, что также будет при экстраполяции влево или вправо. Подставив в уравнение регрессии соответствующие значения х, можно определить выровненные (предсказанные) значения результативного показателя y(x) для каждого наблюдения. Связь между у и х определяет знак коэффициента регрессии b (если > 0 – прямая связь, иначе - обратная). Важная характеристика экономических процессов – эластичность, которая показывает, на сколько процентов изменится зависимая переменная Y при увеличении влияющей переменной Х на 1 % : Э = (ΔY / Y) / (ΔX / X) Применение компьютера позволяет вычислить эластичность по всему диапазону Х, а не только средние значения, как при ручном счете. В качестве Х и Y берутся их средние значения на соответствующих интервалах ΔX и ΔY, расчет ведется по аппроксимирующей функции Ŷ: Э = (Ŷ1 – Ŷ0)/( Ŷ1+ Ŷ0)/(Х1 – Х0)*(Х1+Х0) где индексы 0 и 1 относятся к первым двум значениям переменных Х и Ŷ. Затем формула копируется на весь диапазон, кроме последней ячейки; в Модели1 расчет начинается с температуры 10о. Графики показывают, что расчет эластичности по разным моделям приводит к различным результатам. Обычно экономисты используют среднюю эластичность , Где Y/ X – средний наклон функции Ŷ = f(X). Применение функции эластичности позволяет изучать влияние добавок Х на изменение Y при различных значениях влияющей переменной. 47.Оценка коэффициентов модели Самуэльсона-Хикса Концептуальная модель Самуэльсона-Хикса: 1) Текущее потребление объясняется уровнем ВВП в предыдущем периоде, возрастая вместе с ним, но с меньшей скоростью; 2) Величина инвестиций прямо пропорциональна приросту ВВП за предшествующий период (прирост ВВП за предшествующий период – это разность Yt-1 – Yt-2); 3) Государственные расходы возрастают с постоянным темпом роста; 4) текущее значение ВВП есть сумма текущих уровней потребления, инвестиций и государственных расходов (тождество системы национальных счетов). В сокращённом виде: Потребление = a0 + a1 * ВВП(t-1) Инвестиции = b * ( ВВП(t-1) – ВВП(t-2)) = b * (рост ВВП в прошлом году) Госрасходы = g * Госрасходы (t-1) ВВП = Потребление + Инвестиции + Госрасходы 48. Ошибки от включения в модель незначимых переменных или исключения значимых.с.80 Как обнаружить мультиколлинеарность? Проще всего – по корреляционной матрице. Если коэффициенты корреляции регрессоров больше 0,7, значит они взаимосвязаны. Числовой характеристикой мультиколлинеарности может служить определитель корреляционной матрицы. Если он близок к 1, то регрессоры независимы; если к 0, значит они связаны сильно. Как бороться с мультиколлинеарностью? 1. Смириться, принять во внимание и ничего не делать. 2. Увеличить объём выборки: дисперсии коэффициентов обратно пропорциональны количеству замеров. 3. Удалять из модели регрессоры, слабо коррелирующие с зависимой переменной, или коэффициенты которых имеют малую t-статистику. Как видно из таблицы 7.10, при этом происходит смещение коэффициентов при значимых регрессорах, и возникает вопрос об их экономическом смысле. (А смысл такой: если регрессоры коррелируют и вы можете ими управлять, например, расходы на станки и рабочих, то придётся изменять их пропорционально). F-статистика, то есть качество модели, при этом растёт. 4. Использовать в уравнении регрессии агрегаты из коррелирующих переменных: линейные комбинации с коэффициентами, обратно пропорциональными стандартным отклонениям переменных и выравнивающими их масштабы. Такие агрегаты обычно не имеют экономического смысла, но могут повысить адекватность модели. 5. Факторный анализ, или Метод главных компонент. Используется, если переменных много, но они являются линейными комбинациями небольшого количества независимых факторов, может быть, не имеющих экономического смысла. На Рисунке 7.6 приведён пример: имеется три ортогональных вектора Z1, Z2, Z3 и пять векторов X1, X2, X3, X4, X5, которые можно представить как линейные комбинации из Z1, Z2, Z3. 49. Исследование множественной регрессионной модели с.74-79. Термин ''множественная регрессия'' объясняется тем, что анализу подвергается зависимость одного признака (результирующего) от набора независимых (факторных) признаков. Разделение признаков на результирующий и факторные осуществляется исследователем на основе содержательных представлений об изучаемом явлении (процессе). Все признаки должны быть количественными (хотя допускается и использование дихотомических признаков, принимающих лишь два значения, например 0 и 1). 50. Мультиколлинеарность: чем плоха, как обнаружить и как бороться. Мультиколлинеарность – это взаимная зависимость влияющих переменных. Проблема состоит в том, что при её наличии становится сложно или невозможно разделить влияние регрессоров на зависимую переменную, и коэффициенты теряют экономический смысл предельной функции или эластичности. Дисперсии коэффициентов растут, сами коэффициенты, оценённые по различным выборкам или методом Монте-Карло, коррелируют между собой. Это приводит к тому, что в области настройки модели графики Y и Ŷ прекрасно совпадают, R2 и F высокие, а в области прогноза графики могут совпасть, что можно объяснить взаимным подавлением погрешностей или расходятся, то есть модель оказывается неадекватной. Как обнаружить мультиколлинеарность? Проще всего – по корреляционной матрице. Если коэффициенты корреляции регрессоров больше 0,7, значит они взаимосвязаны. Числовой характеристикой мультиколлинеарности может служить определитель корреляционной матрицы. Если он близок к 1, то регрессоры независимы; если к 0, значит они связаны сильно. Как бороться с мультиколлинеарностью? 1. Смириться, принять во внимание и ничего не делать. 2.Увеличить объём выборки: дисперсии коэффициентов обратно пропорциональны количеству замеров. 3.Удалять из модели регрессоры, слабо коррелирующие с зависимой переменной, или коэффициенты которых имеют малую t-статистику. Как видно из таблицы 7.10, при этом происходит смещение коэффициентов при значимых регрессорах, и возникает вопрос об их экономическом смысле. (А смысл такой: если регрессоры коррелируют и вы можете ими управлять, например, расходы на станки и рабочих, то придётся изменять их пропорционально). F-статистика, то есть качество модели, при этом растёт. 4.Использовать в уравнении регрессии агрегаты из коррелирующих переменных: линейные комбинации с коэффициентами, обратно пропорциональными стандартным отклонениям переменных и выравнивающими их масштабы. Такие агрегаты обычно не имеют экономического смысла, но могут повысить адекватность модели. 5.Факторный анализ, или Метод главных компонент. Используется, если переменных много, но они являются линейными комбинациями небольшого количества независимых факторов, может быть, не имеющих экономического смысла. 51. Признаки стационарности стохастического процесса. Что такое «Белый шум»? с.100 Временной ряд – это конечная реализация cтохастического процесса: генерации набора случайных переменных Y(t). Стохастический процесс может быть стационарным и нестационарным. Процесс является стационарным, если
3. Нет периодических флуктуаций. Распознавание стационарности: 1. График: систематический рост или убывание, волны и зоны высокой волатильности (дисперсии) в длинном ряде сразу видны. 2. Автокорреляция (убывает при росте лага) 3. Тесты тренда: проверка гипотезы о равенстве нулю коэффициента при t. 4. Специальные тесты, включённые в пакеты компьютерных программ Stata, EViews и др., например, тест Дики-Фуллера (Dickey-Fuller) на единичный корень (Unit root). Чисто случайный процесс, стационарный с отсутствием автокорреляции (Cor(ui/uk) = 0) называется Белый шум. Пример нестационарного процесса – случайное блуждание |

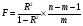 ( 3.3 )
( 3.3 )