1. Метод наименьших квадратов алгоритм метода условия применения

• Название: 1. Метод наименьших квадратов алгоритм метода условия применения
• Анкор: Ekonometrika.docx
• Дата: 26.05.2018
• Размер: 281.01 Kb.
• Имя файла: Ekonometrika.docx
• Тип: Документы; #19683
• страница: 5 из 5

Y(t) = Y(t-1) + a(t) где a(t) – белый шум.

Интересно, что процесс Y(t) = 0,999*Y(t-1) + a(t) является стационарным

Принципиальную возможность избавиться от нестационарности называют интегрируемость. Применяют различные способы избавления от нестационарности:

1. Вычитание тренда, что мы и делали в предыдущем разделе;

2. Использование разностей 1-го, 2-го и т.д. порядков, что можно делать только после сглаживания временного ряда (или энергетического спектра), иначе все эффекты будут подавлены статистическими флуктуациями: дисперсия разности равна сумме дисперсий.

Для исследования рядов цен на фондовом рынке применяются модели, использующие белый шум и авторегрессию, то есть взаимную зависимость уровней временного ряда.

Модель MA(q) (moving average) – линейная комбинация последовательных элементов белого шума

X(t) = a(t) – K(1)*a(t-1) – …. – K(q)*a(t-q)

Модель AR(p) (авторегрессия): линейная комбинация лаговых переменных

X(t) = b0 + b1*X(t-1) + …. + bp*X(t-p)

Особенно популярны их комбинации

ARMA(p,q) = AR(p) + MA(q)

и ARIMA(p, i ,q): то же, с интегрируемостью i –го порядка.

52. Структурная и приведённая формы спецификации эконометрических моделей.

Система совместных, одновременных уравнений (или структурная форма модели) обычно содержит эндогенные и экзогенные переменные.

Эндогенные переменные – это зависимые переменные, число которых равно числу уравнений в системе и которые обозначаются через , взаимозависимые переменные, которые определяются внутри модели (системы).

Экзогенные переменные – это предопределенные переменные, влияющие на эндогенные переменные, но не зависящие от них, независимые переменные, которые определяются вне системы. Обозначаются через .

В качестве экзогенных переменных могут рассматриваться значения эндогенных переменных за предшествующий период времени (лаговые переменные).

Предопределенными переменными наз. экзогенные и лаговые эндогенные переменные сис-мы.

Структурная форма модели позволяет увидеть влияние изменений любой экзогенной переменной на значения эндогенной переменной.

Структурная форма модели в правой части содержит при эндогенных переменных коэффициенты и экзогенных переменных – коэффициенты , которые называются структурными коэффициентами модели. Все переменные в модели выражены в отклонениях от среднего уровня, т.е. под подразумевается , а под – соответственно . Поэтому свободный член в каждом уравнении системы отсутствует. (3.3) ниже представлено.



Использование МНК для оценивания структурных коэффициентов модели дает, как принято считать в теории, смещенные и несостоятельные оценки. Поэтому обычно для определения структурных коэффициентов модели структурная форма модели преобразуется в приведенную форму модели.

Приведенная форма модели представляет собой систему линейных функций эндогенных переменных от экзогенных: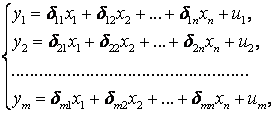

(3.4)

где – коэффициенты приведенной формы модели, – остаточная величина для приведенной формы.

По своему виду приведенная форма модели ничем не отличается от системы независимых уравнений, параметры которой оцениваются традиционным МНК. Применяя МНК, можно оценить , а затем оценить значения эндогенных переменных через экзогенные.

Коэффициенты приведенной формы модели представляют собой нелинейные функции коэффициентов структурной формы модели.

Структурные модели можно подразделить на три вида: - идентифицируемые;-неидентифиц.;- сверхидентифицируемые.

Условие идентифицируемости модели может быть записано в виде следующего правила:

Предопределённых + 1 = Эндогенных идентифицируемо

 Предопределённых + 1 < Эндогенных неидентифицируемо

Предопределённых + 1 > Эндогенных сверхидентифицируемо

53. Алгоритм проверки значимости регрессора в парной регрессионной модели. По t-статистике, по F-статистике.

При проверке качества спецификации парной регрессии наиболее важной является задача установления наличия линейной зависимости между эндогенной переменной и регрессором модели. С этой целью проверяют значимость оценки параметра b (при регрессоре модели).

Алгоритм проверки значимости параметра b выполняется в следующей последовательности:

1) оценка параметров парной регрессии

2) оценка дисперсии возмущений S²

3) оценка 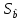среднего квадратичного отклонения параметра b

4) выбор значения t_кр (по заданному уровню значимости 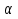и числу степеней свободы (n-2) из таблиц распределения Стьюдента)

5) проверка неравенства 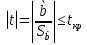при Н0: b=0

Если данное неравенство выполняется, то регрессор признается незначимым, если не выполняется, то данная гипотеза отвергается и регрессор признается значимым, т.е. между эндогенной переменной и регрессором присутствует линейная зависимость.

54.Свойства рядов цен на фондовом рынке. Принципы построения портфеля Марковица С.93,102

Применяемый алгоритм при анализе временных рядов цен на фондовом рынке с использованием автокорреляций высоких порядков с целью обоснования методов прогнозирования с применением волнообразных колебаний:

1. Считывание временных рядов из торговой системы, например, FINAM.

2. Оценка целесообразности работы с рядом, отбраковка рядов с резкими скачками цен и с отсутствием волнообразных колебаний.

3. Вычитание трендов.

4. Проверка остатков на стационарность (см.раздел 8.3).

5. Расчёт автокорреляций и построение коррелограмм

6. Классификация рядов и коррелограмм.

7. Оценка целесообразности применения методов технического анализа с использованием волнообразных колебаний.

8. Аппроксимация участка ряда функцией с синусоидой.

9. Оценка точности аппроксимации и прогноза.
Доходность портфеля определяется как сумма доходностей ценных бумаг, его составляющих, взвешенных на их доли в портфеле:

D = Σd_ix_i

Требуется составить оптимальный портфель ценных бумаг по известным доходностям ценных бумаг за некоторый промежуток времени, имеющий максимальную доходность при заданном риске (портфель Марковица), или заданную доходность при минимальном риске. Мерой риска доходности одной бумаги является стандартное отклонение значений доходностей за некоторый промежуток времени. Если имеется тренд, то есть ряд не является стационарным, то его надо вычесть, а потом вычислять риск (СКО).

При отсутствии взаимной зависимости доходностей ценных бумаг (т.е. при нулевых коэффициентах корреляции) суммарная дисперсия равна сумме дисперсий S² =  х_i ² *S_i² , где х_i – количество (или процент) закупаемых ценных бумаг i-ой фирмы. При коэффициентах корреляции, равных 1 суммарное стандартное отклонение (риск портфеля) S равно сумме стандартных отклонений S_i с соответствующими знаками. При составлении портфеля из ценных бумаг двух фирм квадрат риска равен

S² = x₁²*S₁² + x₂²*S₂² + 2x₁*x₂* Cov(d1,d2),

где ковариация Cov(d1,d2) = ( (d1i – d1cp)*(d2i – d2cp))/(N – 1 )

Если портфель составляется из ценных бумаг большего количества n фирм, то дисперсия портфеля (квадрат риска) вычисляется по формуле

S²=   x_i*x_j* Cov(di,dj). Обозначим b_ij = Cov(di,dj), тогда

S² = x₁*x₁*b₁₁ + x₁*x₂*b₁₂ + … + x₁*x_n*b_1n

+ x₂*x₁*b₂₁ + x₂*x₂*b₂₂ + … + x₂*x_n*b_2n

………………………………………………….

+ x_n*x₁*b_n1 + x_n*x₂*b_n2 + … + x_n*x_n*b_nn
55.Динамическая модель из одновременных линейных уравнений (привести пример) с.105.

Многие экономические модели требуют для своего описания систем взаимосвязанных уравнений. Для настройки этих моделей обычно используют временные ряды уровней различных переменных, часть которых принимают за эндогенные, а часть за экзогенные. Выбор переменных определяется исследователем, но обычно экзогенные переменные или не зависят от нас (температура воздуха, курс доллара, цена нефти), или мы можем ими управлять (инвестиции, выпуск продукции).

В качестве примера рассмотрим Модель спроса и предложения на конкурентном рынке, а также рыночной цены (p) в зависимости от величины дохода (x) на душу населения. Её называют “паутинной моделью”, так как движение спроса и предложения к равновесию в соответствующей системе координат напоминает паутину. Пример взят из учебника В.А.Бывшева [2].

Изменение во времени спроса, предложения и цены на конкурентном рынке закреплено в следующих утверждениях экономической теории:

1. 
   Текущий уровень спроса объясняется текущей ценой товара и текущим располагаемым доходом на душу населения, причём спрос падает с ростом цены и растёт с ростом дохода.
   
2. 
   Текущее предложение объясняется ценой товара в предшествующем периоде и возрастает с ростом этой цены.
   
3. 
   Текущее значение рыночной цены устанавливается при балансе текущего спроса и текущего предложения товара.
   

Кратко это можно записать, с учётом случайных возмущений:

Спрос =a0 + a1· цена + a2· доход +Возмущение1

Предложение = b0 + b1· цена вчера + Возмущение2

Спрос = Предложение (тождество)

Соответствующая система уравнений и тождеств: 
d= a0 + a1· p + a2· x + u1

s = b0 + b1 · p(t-1) + u2 ( 9.1)

d = s

a1<0, a2>0, b1>0

В данном случае d, s, p эндогенные,

x, p(t-1) предопределённые (экзогенная и лаговая)

Второе уравнение является обычным уравнением регрессии, и его можно настраивать, используя обычный метод наименьших квадратов. А с первым уравнением так поступить нельзя, так как в него входят две эндогенных переменных. Такая модель называется структурной, она возникает непосредственно из экономических предпосылок. Требуется преобразовать модель к приведённому виду, где в левой части будут стоять эндогенные переменные, а в правой – предопределённые. Можно решать эту задачу путём последовательной замены эндогенных переменных. Мы рассмотрим метод, основанный на преобразовании матриц. Объединим эндогенные переменные в вектор Y, а предопределённые – в вектор Х:
Y= (d, s, p) ; X = (1, p(t-1), x)

Единица в векторе Х появилась, чтобы работать с коэффициентами a0 и b0. В матричном виде система уравнений и тождеств выглядит
AY + BX =0
или
1· d + 0· s - a1· p + (- a0) ·1 + 0 ·p(t-1) + (-a2)· x = 0

0 ·d + 1· s + 0· p + (- b0) · 1 + (-b1) · p(t-1) + 0· x = 0

1 ·d + (-1) · s +0 ·p + 0 · 1 + 0· p(t-1) + 0· x = 0

Здесь матрицы А и В:
1 0 -a1 - a0 0 -a2

A 0 1 0 B - b0 -b1 0

1 -1 0 0 0 0

Приведённая форма модели Y = M X. Компоненты матрицы М
0 1 2

M 0 1 2

0 1 2

получим преобразованием М = А^-1В, где А^-1 означает обратную к А матрицу. Приведённая форма модели:

d = 0 + 1· p(t-1) + 2· x

s = 0 + 1· p(t-1) + 2· x

p = 0 + 1· p(t-1) + 2· x

где

0 = b0 ; 1 =b1 ; 2 = 0 ;

0 = (b0-a0)/a1 ; 1 =b1/a1; 2 = - a2/a1

56. Метод наибольшего правдоподобия: принципы и целесообразность использования

Метод наибольшего правдоподобия -- метод поиска модели, наилучшим в каком-то смысле образом описывающей обучающую выборку, полученную с некоторым неизвестным распределением.

Описание метода Пусть на вход подается некоторая величина x, а на выходе имеется величина y. Также существует условная вероятность , описывающая вероятность получить на выходе величину y, если на вход была подана величина x. Если множество величин не дискретно, то условная вероятность заменяется на условную плотность распределения. Считается, что эта условная вероятность нам неизвестна. Пусть имеется некоторое множество моделей, описываемых различными условными вероятностями , где играет роль индекса, приписываемого конкретной модели, и может вообще говоря иметь любую природу. Пусть также существует обучающая выборка порождённая с неизвестной условной вероятностью . Причем, считается, что все пары порождаются независимо. Требуется на основании обучающей выборки выделить из множества моделей (то есть выбрать ) ту, что наилучшим образом подходит к обучающей выборке. Функцией правдоподобия называется функция вида . Метод наибольшего правдоподобия состоит в том, что из множества моделей выбирается та, что максимизирует значение функции правдоподобия, т.е. выбирается значение параметра

Обоснование метода Заметим, что в силу независимости элементов обучающей выборки вероятность получить набор выходных значений при поданных на вход значениях равняется . Из эвристических соображений понятно, что, чем ближе модель к истинной, тем больше должна быть эта величина. Функция правдоподобия является логарифмом этой величины. Можно также показать, что если среди множества моделей есть истинная, то максимум математического ожидания функции правдоподобия действительно достигается на истинной модели.


57. Этапы исследования модели множественной регрессии с.74-79.
1. Построить корреляционную матрицу по всем переменным, включая время. Построить графики всех переменных в зависимости от времени. Выбрать вид модели.
2. Выбрать мультипликативную модель и линеаризовать её логарифмированием:

Ln Ŷ = Ln b0+ b1*LnX1+b2*LnX2+b3*LnX3+b4*LnX4

после переобозначения

Z^ = a + b1V1 + b2V2 +b3V3 + b4V4
3. Построить корреляционную матрицу

t V1 V2 V3 V4 Z

t 1

V1 0,995 1

V2 0,879 0,882 1

V3 0,926 0,932 0,968 1

V4 0,983 0,973 0,898 0,938 1

Z 0,924 0,912 0,661 0,774 0,877 1