1. Метод наименьших квадратов алгоритм метода условия применения
 Скачать 281.01 Kb. Скачать 281.01 Kb.
|
Алгоритм теста Голдфелда-Квандта на наличие (отсутствие) гетероскедастичности случайных возмущений.Гипотеза(1): 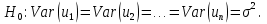 Шаг 1. Уравнения наблюдений объекта 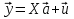 следует упорядочить по возрастанию суммы модулей значений предопределенных переменных модели (2), следует упорядочить по возрастанию суммы модулей значений предопределенных переменных модели (2),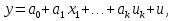 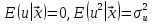 т.е. по возрастанию значений 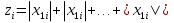 Шаг 2. По первым 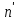 упорядоченным уравнениям наблюдений объекта вычислить МНК-оценки параметров модели и величину упорядоченным уравнениям наблюдений объекта вычислить МНК-оценки параметров модели и величину 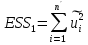 где где 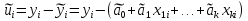 - МНК-оценка случайного возмущения - МНК-оценка случайного возмущения 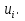 Шаг 3. По последним 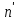 упорядоченным уравнениям наблюдений вычислить МНК-оценки параметров модели и величину упорядоченным уравнениям наблюдений вычислить МНК-оценки параметров модели и величину 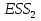 (аналогично). (аналогично).Шаг 4. Вычислить статистику, для этого делим большее на меньшее, к примеру, если ESS1больше ESS2: 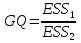 . .Шаг 5. Задаться уровнем значимости 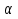 и с помощью функции FРАСПОБР Excel при количествах степеней свободы и с помощью функции FРАСПОБР Excel при количествах степеней свободы 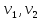 , где , где 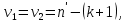 определить (1- определить (1-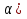 -квантиль, -квантиль, 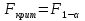 распределения Фишера. распределения Фишера.Шаг 6. Принять гипотезу (1), если справедливы неравенства 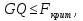 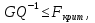 Т.е. при справедливых неравенствах случайный остаток в модели (2) полагать гомоскедастичными. В противном случае гипотезу (1) отклонить как противоречащую реальным данным и сделать вывод о гетероскедастичности случайного остатка в модели (2). 25. Спецификация и оценивание МНК эконометрических моделей нелинейных по параметрам. В моделях, нелинейных по параметрам, например степенных или показательных, непосредственное применение МНК(метод наименьших квадратов) для их оценки невозможно, так как необходимым условием применимости МНК является линейность по коэффициентам уравнения регрессии. В данном случае преобразованием, которое приводит уравнение регрессии к линейному виду, является логарифмирование. Логарифмические модели:Y = AXb, где А и b— параметры модели. Прологарифмируем обе части данного уравнения: ln(Y)=ln(A) + b*ln(X) = a+b*ln(X), где а= ln(A) (*). Спецификация, соответствующая (*) называется двойной логарифмической моделью: ln(Y)= a+ b*ln(X)+u, поскольку и эндогенная переменная, и регрессор используются в логарифмической форме. Введем обозначения: Y*=ln(Y), X*=ln(X) Y*=a+b*X+u Получаем спецификацию линейной модели, к которой при соответствующем включении случайного возмущения применим МНК. В моделях, нелинейных по оцениваемым параметрам, но приводимых к линейному виду, МНК применяется к преобразованным уравнениям. Пусть получена МНК-оценка модели Y*=a+b*X+u: y*=ā + bx+u (Sā) (Sb) (Su) Коэффициенты исходной модели и их стандартные ошибки вычисляются с учетом замены. Нелинейный МНК.В общем случае оценка нелинейных по параметрам уравнений выполняется с помощью так называемого нелинейного метода наименьших квадратов (НМНК). Обозначим нелинейное по параметрам уравнение регрессии f(X, ß) (X— матрица рсгрсссоров,ß — вектор параметров). Параметры уравнений в данном методе подбираются таким образом, чтобы максимально приблизить кривую f(X, ß) к результатам наблюдений эндогенной переменной Y. Таким образом, здесь, как и в обычном МНК, минимизируется сумма квадратов отклонений: F=2 (**) Если продифференцировать F по параметрам и приравнять производные нулю, то получим нелинейную систему нормальных уравнений. В случае линейного уравнения регрессии нормальные уравнения представляли собой систему линейных уравнений, решение которой не составляло труда. Нелинейный метод наименьших квадратов сводится к задаче минимизации функции (**) нескольких переменных ß=(ß1,…,ßn) 26. Способы корректировки гетероскедастичности. Метод взвешенных наименьших квадратов Понятия “гетероскедастичность” и “автокорреляция” актуальны, если массивы данных упорядочены, что имеет место для временных рядов. “Пространственные” данные можно искусственно упорядочить, например, отсортировав их по возрастанию какой-либо переменной; при этом можно выявить кластеры с аномальной дисперсией остатков, что может означать неоднородность выборки или неадекватность модели. Считается, что гетероскедастичность может привести к снижению эффективности оценок коэффициентов, и надо её искусственно подавлять. Эта технология называется Взвешенный метод наименьших квадратов (ВМНК) и обычно используется в матричном варианте МНК. При обнаружении автокорреляции остатков применяется Обобщённый метод наименьших квадратов ОМНК, основанный на преобразовании матриц, но с учётом корреляций остатков. ВМНК- математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от искомых переменных. Он может использоваться для «решения» переопределенных систем уравнений (когда количество уравнений превышает количество неизвестных), для поиска решения в случае обычных (не переопределенных) нелинейных систем уравнений, для аппроксимации точечных значений некоторой функцией. МНК является одним из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным. 27.Проблема мультиколлинеарности в моделях множественной регрессии.признаки мультиколлениарности. Множественная регрессия позволяет построить и проверить модель линейной связи между зависимой (эндогенной) и несколькими независимыми (экзогенными) переменными: y = f(x1,...,xр ), где у - зависимая переменная (результативный признак); х1,...,хр - независимые переменные (факторы). Множественная линейная регрессионная модель имеет вид: y=a+b1x1+b2x2+…+bpxp+ε Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям: 1. быть количественно измеримы. При включении качественного фактора нужно придать ему количественную определенность 2. не должны быть коррелированы между собой и тем более и годиться в точной функциональной связи. Включение в модель факторов с высокой интеркорреляцией, когда ryx1 < rx1x2 может повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии. Поскольку одним из условий построения уравнения множественной регрессии является независимость действия факторов, коллинеарность факторов нарушает это условие. Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. Признаки мультиколлинеарности. 1.В модели с двумя переменными одним из признаков мультиколлинеарности является близкое к единице значение коэффициента парной корреляции. Если значение хотя бы одного из коэффициентов парной корреляции больше, чем 0,8, то мультиколлинеарность представляет собой серьезную проблему. Однако в модели с числом независимых переменных больше двух, парный коэффициент корреляции может принимать небольшое значение даже в случае наличия мультиколлинеарности. В этом случае лучше рассматривать частные коэффициенты корреляции. 2. Для проверки мультиколлинеарности можно рассмотреть детерминант матрицы коэффициентов парной корреляции |r|. Этот детерминант называется детерминантом корреляции |r| ∈(0; 1). Если |r| = 0, то существует полная мультиколлинеарность. Если |r|=1, то мультиколлинеарность отсутствует. Чем ближе |r| к нулю, тем более вероятно наличие мультиколлинеарности. 3. Если оценки имеют большие стандартные ошибки, невысокую значимость, но модель в целом значима (имеет высокий коэффициент детерминации), то это свидетельствует о наличие мультиколлинеарности. 4. Если введение в модель новой независимой переменной приводит к существенному изменению. 28.Что такое логит,тобит,пробит. Логит-модель— эконометрическая модель, относящаяся к классу таких моделей, для анализа которых неприменимы обычные методы регрессионного анализа. Отличие ее состоит в том, что в ней зависимая переменная может принимать лишь ограниченное число значений, в простейшем случае — либо 0, либо 1 Задача состоит в том, чтобы определить вероятность принятия зависимой переменной значения 0 или 1. Здесь в качестве аналитического средства применяется логистическая функция (выраженная в логарифмической форме), отсюда и название. Тобит-модели— один из видов эконометрических моделей, не поддающихся исследованию стандартными методами регрессионного анализа, поскольку включают переменные, представляющие собой смесь дискретных и непрерывных величин. Например, таковы модели рынков, на которых часть цен лимитированы, а часть — свободны. Пробит-модели - вид эконометрических моделей, которые не поддаются исследованию стандартными методами регрессионного анализа, поскольку содержат дихотомические переменные (все или ничего). Примеры — модели принятия решений: владеть собственностью или арендовать ее, модели выбора маршрута путешествия или выбора профессии 29. Что такое Метод наибольшего правдоподобия стр. 62. Метод максимального правдоподобия или метод наибольшего правдоподобия (ММП, ML, MLE — англ. maximum likelihood estimation) в математической статистике — это метод оценивания неизвестного параметра путём максимизации функции правдоподобия[1]. Основан на предположении о том, что вся информация о статистической выборке содержится в функции правдоподобия. Метод максимального правдоподобия был проанализирован, рекомендован и значительно популяризирован Р. Фишером Оценка максимального правдоподобия является популярным статистическим методом, который используется для создания статистической модели на основе данных, и обеспечения оценки параметров модели. Метод максимального правдоподобия соответствует многим известным методам оценки в области статистики. Например, вы интересуетесь таким антропометрическим параметром, как рост жителей России. Предположим, у вас имеются данные о росте некоторого количества людей, а не всего населения. Кроме того предполагается, что рост является нормально распределенной величиной с неизвестной дисперсией и средним значением. Среднее значение и дисперсия роста в выборке являются максимально правдоподобными к среднему значению и дисперсии всего населения. Для фиксированного набора данных и базовой вероятностной модели, используя метод максимального правдоподобия, мы получим значения параметров модели, которые делают данные «более близкими» к реальным. Оценка максимального правдоподобия дает уникальный и простой способ определить решения в случае нормального распределения. Метод оценки максимального правдоподобия применяется для широкого круга статистических моделей, в том числе: • линейные модели и обобщенные линейные модели; • факторный анализ; • моделирование структурных уравнений; • многие ситуации, в рамках проверки гипотезы и доверительного интервала формирования; • дискретные модели выбора. 30. Что такое стационарный процесс? Стационарность — свойство процесса не менять свои характеристики со временем. Имеет смысл в нескольких разделах науки. Стационарность случайного процесса означает неизменность во времени его вероятностных закономерностей Временной ряд – это конечная реализация стохастического процесса: генерации набора случайных переменных Y(t). Стохастический процесс может быть стационарным и нестационарным. Процесс является стационарным, если 1. Математическое ожидание значений переменных не меняется. 2. Математическое ожидание дисперсий переменных не меняется. 3. Нет периодических флуктуаций. Распознавание стационарности: 1. График: систематический рост или убывание, волны и зоны высокой волатильности (дисперсии) в длинном ряде сразу видны. 2. Автокорреляция (убывает при росте лага) 3. Тесты тренда: проверка гипотезы о равенстве нулю коэффициента при t. 4. Специальные тесты, включённые в пакеты компьютерных программ Stata, 31.Свойства временных рядов. Эконометрическую модель можно построить, используя три типа исходных данных: - данные, характеризующие совокупность различных объек тов в определенный момент (период) времени: crosssectionaldata, “пространственные”; - данные, характеризующие один объект за ряд последова тельных моментов (периодов) времени: временные ряды, timeseries;
Временной ряд – это совокупность значений какого-либо показателя за несколько последовательных моментов (периодов) времени. Он формируется под воздействием большого числа факторов, которые можно условно подразделить на три группы:
Модели, которые построены по данным, характеризующим один объект за ряд последовательных периодов, называются моделями временных рядов. Каждый уровень временного ряда может формироваться их трендовой (Т), циклической или сезонной компоненты (S), а также случайной (E) компоненты. Модели, где временной ряд представлен в виде суммы перечисленных компонентов называются аддитивными, если в виде произведения – мультипликативными моделями. Аддитивная модель имеет вид: Y=T+S+E Мультипликативная модель имеет вид: Y=T*S*E Построение модели временного ряда:
Построение аналитической функции при моделировании тренда в любой задаче по эконометрике на временные ряды называют аналитическим выравниванием временного ряда и в основном применяются функции: линейная, степенная, гиперболическая, параболическая и т.д. Параметры тренда определяются как и в случае линейной регрессии методом МНК, где в качестве независимой переменной выступает время, а в качестве зависимой переменной – уровни временного ряда. Критерием отбора наилучшей формы тренда служит наибольшее значение коэффициента детерминации, критерии Фишера и Стьюдента. Автокорреляция в остатках – корреляционная зависимость между значениями остатков за текущий и предыдущие моменты времени. Для определения автокорреляции остатков используется критерий Дарбина-Уотсона: 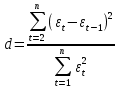 Временной ряд – это датированная целочисленными моментами времени t экономическая переменная . Эта переменная служит количественной характеристикой некоторого экономического объекта, поэтому изменение этой переменной во времени определяется факторами, оказывающими воздействие на данный объект с ходом времени. Все факторы делятся на 3 класса. 1 класс: факторы («вековые» воздействия), результирующее влияние которых на данный объект на протяжении длительного отрезка времени не изменяют своего направления. Они порождают монотонную составляющую (тенденцию или тренд). 2 класс: факторы (циклические воздействия), результирующее влияние которых на объект совершает законченный круг в течение некоторого фиксированного промежутка времени T. 3 класс: факторы (случайные воздействия),результирующее влияние которых на объект с высокой скоростью меняет направление и интенсивность. 3 Класс факторов позволяют интерпретировать величину в каждый период времени как случайную переменную 32.Модели AR и VAR . Авторегрессионная (AR-) модель (англ. Autoregressive model) — модель временных рядов, в которой значения временного ряда в данный момент линейно зависят от предыдущих значений этого же ряда. Авторегрессионный процесс порядка p (AR(p)-процесс)- определяется следующим образом Xt=c+∑i=1paiXt−i+εt, где a1,…,ap — параметры модели (коэффициенты авторегрессии), c -постоянная (часто для упрощения предполагается равной нулю), а εt — белый шум. Модель AR(p) (авторегрессия): линейная комбинация лаговых переменных X(t) = b0 + b1*X(t-1) + …. + bp*X(t-p) Особенно популярны их комбинации ARMA(p,q) = AR(p) + MA(q) и ARIMA(p, i ,q): то же, с интегрируемостью i –го порядка. Особый интерес представляет модель векторная авторегрессия VAR, состоящая из многих уравнений, в которой левые (эндогенные) переменные зависят и от своих, и от чужих лаговых значений. |
