Синтез линейной САУ леккция. Синтез линейных САУ. Синтез линейных стационарных систем автоматического управления
 Скачать 194.45 Kb. Скачать 194.45 Kb.
|
|
Синтез линейных стационарных систем автоматического управления. Общие положения. Под синтезом САУ понимается направленный расчет, имеющий конечной целью определение структуры и параметров системы, удовлетворяющий некоторым заранее сформулированным требованиям. Существует множество подходов к синтезу и множество вариантов постановки задачи синтеза. Синтез можно рассматривать как процесс решения некоторой вариационной задачи, позволяющий получить систему оптимальную по некоторому функционалу качества. Так строятся, например, оптимальные по быстродействию САУ. Синтез можно рассматривать также как инженерную задачу, сводящуюся к такому построению САУ, которое обеспечивает предъявляемое к ней требование технического задания. Эта задача может включать выбор измерительных, усилительных, управляющих устройств, т.е. всех элементов системы за исключением объекта. Вместе с тем, в понятие синтеза часто вкладывается еще более узкий смысл и рассматривается задача определения только структуры и параметров корректирующего устройства, которое необходимо добавить к имеющийся неизменяемой части системы (объекту с регулятором), чтобы обеспечить требуемые динамические качества САУ. В нашем курсе мы ограничимся рассмотрением именно этой задачи. Способы включения корректирующих устройств. Корректирующие устройства могут вводиться в систему управления различными способами. На рис. 1 представлена схема введения в замкнутую систему последовательного корректирующего устройства.  Рис. 1 Здесь 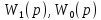 - передаточные функции отдельных частей исходной системы (например, регулятора и объекта управления), - передаточные функции отдельных частей исходной системы (например, регулятора и объекта управления), 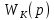 - передаточная функция корректирующего устройства. - передаточная функция корректирующего устройства.На рис. 2. показана схема параллельного корректирующего устройства, а на рис. 3. – схема включения корректирующего устройства в цепь местной обратной связи. При этом местная обратная связь может быть как отрицательной, так и положительной. 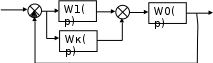 Рис.2 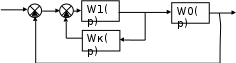 Рис.3 Передаточная функция разомкнутой системы W(p) для каждого из рассмотренных вариантов включения корректирующего устройства имеет вид: -при последовательном включении: 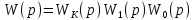 ; ;-при параллельном включении: 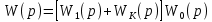 ; ;-при включении в местную обратную связь: 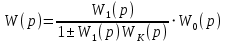 Использование того или иного типа корректирующего устройства определяется, в основном, удобством его технической реализации. Дело в том, что в линейных системах их динамические свойства могут быть сделаны одинаковыми при корректирующих свойствах различного типа. Для этого нужно только подобрать передаточную функцию корректирующих устройств так, чтобы были равны эквивалентные передаточные функции разомкнутой системы. Например, если 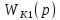 - передаточная функция последовательного, а - передаточная функция последовательного, а 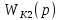 - параллельного корректирующих устройств, то данная эквивалентность будет достигнута, если - параллельного корректирующих устройств, то данная эквивалентность будет достигнута, если , ,т.е. 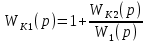 . .Аналогичные формулы могут быть получены и для остальных 5 сочетаний типов включения. В качестве корректирующих устройств в недавнем прошлом наиболее широко использовались пассивные R,C,L-цепи (особенно RC-цепи). Существует большое число таких корректирующих звеньев. Их схемы и соответствующие передаточные функции приведены в литературе по ТАУ. Типовые законы управления. Рассмотрим структурную схему системы с последовательной коррекцией, объединив передаточные функции 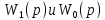 в одну передаточную функцию в одну передаточную функцию  (см. рис. 4). (см. рис. 4). При создании конкретной автоматической системы управляемый объект задан заранее и передаточная функция WH(p) известна. Для придания  Рис.4 всей системе требуемых динамических свойств мы можем выбирать передаточные функции регулятора 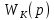 . Подавляющее большинство промышленных систем используют регуляторы первого или второго порядка. Такие регуляторы могут во многих случаях обеспечить необходимое качество управления, они дешевы и легко настраиваются. . Подавляющее большинство промышленных систем используют регуляторы первого или второго порядка. Такие регуляторы могут во многих случаях обеспечить необходимое качество управления, они дешевы и легко настраиваются.Зависимость 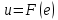 выходной переменной регулятора от его входной величины называется законом или алгоритмом управления. Пусть 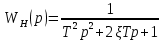 Рассмотрим наиболее распространенные (типовые) законы управления. Пропорциональный закон управления (П – управление) Закон управления определяется зависимостью 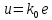 . .При этом передаточная функция разомкнутой системы имеет вид 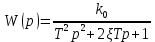 Характеристическое уравнение замкнутой системы 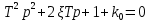 имеет корни 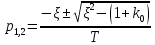 (1) (1)Из (1) видно, что, если объект управления – колебательное звено ( 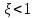 ), то замкнутая САУ при любом ), то замкнутая САУ при любом 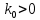 также колебательное звено. Степень колебательности также колебательное звено. Степень колебательности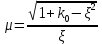 c ростом  возрастает возрастаетПередаточная функция по ошибке имеет вид 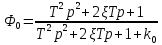 и 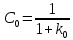 . .Таким образом, при П – регуляторе система статическая и статическая ошибка убывает с ростом  . Но, начиная с . Но, начиная с  , когда замкнутая система становится колебательной, с ростом , когда замкнутая система становится колебательной, с ростом  увеличивается колебательность µ. увеличивается колебательность µ.Следовательно, с ростом  качество системы в установившемся режиме улучшается, а в переходном режиме ухудшается. качество системы в установившемся режиме улучшается, а в переходном режиме ухудшается.При повышении  уменьшаются запасы устойчивости На практике при достаточно высоких требованиях к точности П – управление не обеспечивает нужную точность и нужные запасы устойчивости. уменьшаются запасы устойчивости На практике при достаточно высоких требованиях к точности П – управление не обеспечивает нужную точность и нужные запасы устойчивости.Интегральный закон управления (И - управление) При этом законе управления передаточная функция вводимого в систему корректирующего устройства имеет вид 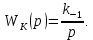 Система становится астатической, передаточная функция разомкнутой системы определяется выражением 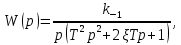 т.е. с точки зрения повышения точности И – управление является желательным. Характеристическое уравнение замкнутой системы имеет вид 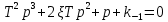 и условие устойчивости определяется неравенством  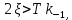 т.е. 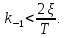 Из последнего выражения следует, что для обеспечения устойчивости 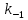 нужно уменьшать, что ведет к уменьшению частоты среза разомкнутой системы и затягиванию переходных процессов. Таким образом, после введения И – управления и обеспечения устойчивости мы получим САУ, отрабатывающую без ошибки постоянные входные сигналы, но с более медленными, чем и П – управлением, переходными процессами. Пропорционально-интегральный закон управления (ПИ- управление) Передаточная функция вводимого в систему корректирующего устройства имеет вид 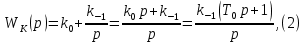 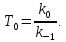 Иногда в литературе такое корректирующее устройство называется изодромным. Передаточная функция разомкнутой САУ имеет вид 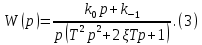 Характеристическое уравнение замкнутой системы 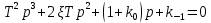 и условие устойчивости определится неравенством 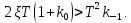 Из последнего неравенства вытекает, что при 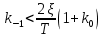 система устойчива система устойчивапри 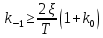 система неустойчива. система неустойчива.Естественно ожидать, что с ростом 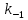 в области устойчивости запасы устойчивости уменьшаются, а колебательность увеличивается. Из зависимости (3) видно, что система является астатической и с ростом в области устойчивости запасы устойчивости уменьшаются, а колебательность увеличивается. Из зависимости (3) видно, что система является астатической и с ростом 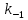 уменьшается скоростная ошибка. При увеличении уменьшается скоростная ошибка. При увеличении 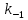 до определенной величины система становится неустойчивой. Однако выбором коэффициентов до определенной величины система становится неустойчивой. Однако выбором коэффициентов 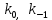 можно получить астататическую систему без заметного или недопустимого ухудшения запасов устойчивости. можно получить астататическую систему без заметного или недопустимого ухудшения запасов устойчивости.Рассмотрим ЛАФЧХ устройства с передаточной функцией (2) (см. рис. 5) 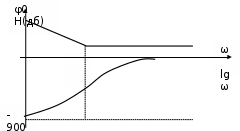 Рис. 5. Из рис. 5 видно, что при относительно большом 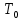 и и 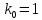 ЛАФЧХ САУ с ПИ – управлением отличаются от ЛАФЧХ исходной САУ только в низкочастотной области. при этом для частот ЛАФЧХ САУ с ПИ – управлением отличаются от ЛАФЧХ исходной САУ только в низкочастотной области. при этом для частот 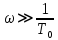 в районе частоты среза исходной САУ вид исходных ЛАФЧХ может быть сохранен. Это соответствует сохранению прежних запасов устойчивости. Частота среза также на меняется или меняется незначительно, а, следовательно, не меняется существенно быстродействие системы. в районе частоты среза исходной САУ вид исходных ЛАФЧХ может быть сохранен. Это соответствует сохранению прежних запасов устойчивости. Частота среза также на меняется или меняется незначительно, а, следовательно, не меняется существенно быстродействие системы.Таким образом. ПИ – управление позволяет сочетать преимущества П и И – законов управления. Его использование приводит к повышению точности при воспроизведении постоянных сигналов при сохранении или незначительном ухудшении других показателей качества регулирования. Пропорционально-дифференциальный закон управления (ПД- управление) В этом случае  и передаточная функция разомкнутой САУ имеет вид 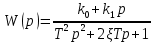 Характеристическое уравнение замкнутой системы 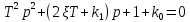 имеет корни 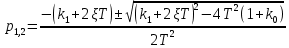 если в последней зависимости подкоренное выражение неотрицательно, т.е. 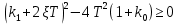 или  система является апериодическим звеном 2 порядка. Если 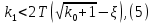 то система является колебательным звеном, у которого степень устойчивости η и колебательность μ принимают вид 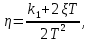 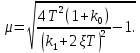 Следовательно, при выполнении условия (5) с ростом 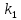 степень устойчивости растет, а колебательность убывает. степень устойчивости растет, а колебательность убывает.При выполнении условия (4) формула для степени устойчивости имеет вид 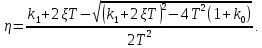 Продифференцировав его по 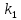 , получим , получим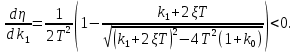 Следовательно, в этом случае с ростом 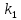 степень устойчивости убывает. степень устойчивости убывает.Передаточная функция замкнутой системы по ошибке имеет вид 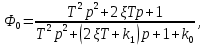 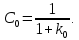 Таким образом, введение производной в закон управления улучшает качество САУ в переходном режиме. На качество в установившемся режиме коэффициент 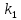 не влияет. Следует, однако, иметь в виду, что при чрезмерном увеличении не влияет. Следует, однако, иметь в виду, что при чрезмерном увеличении 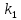 качество системы в переходном режиме может ухудшиться. качество системы в переходном режиме может ухудшиться.Пропорционально – интегрально – дифференциальный закон управления (ПИД - управление) В этом случае 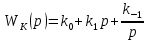 и передаточная функция разомкнутой САУ определяется зависимостью 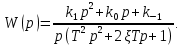 Характеристическое уравнение замкнутой системы имеет вид 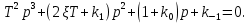 Условием устойчивости замкнутой системы является выполнение неравенства 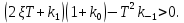 выбором 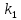 всегда можно обеспечить выполнение данного неравенства, т.е. сделать систему устойчивой. всегда можно обеспечить выполнение данного неравенства, т.е. сделать систему устойчивой.Таким образом, введение в закон управления интегратора может сделать устойчивую систему неустойчивой, а введение дифференцирующего звена может сделать неустойчивую систему устойчивой. Ошибка при воспроизведении постоянного входного сигнала равна нулю, ошибка при входном сигнале 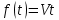 равна равна  . .Основные выводы о влиянии дифференцирующего и интегрирующего звеньев, полученные для ПД и ПИ законов управления, сохраняются и для ПИД - закона, т.е. 1. Введение в закон управления интегрирующего звена делает систему астатической и улучшает ее качество в установившемся режиме, но может сделать систему неустойчивой и ухудшает качество в переходном режиме. 2. Введение в закон управления дифференцирующего звена оказывает стабилизирующее влияние (может сделать неустойчивую систему устойчивой) и улучшает качество в переходном режиме, не оказывая влиянии на качество в установившемся режиме. Эти выводы получены для системы с объектов управления второго порядка, но, в основном, они справедливы и в общем случае, когда объект описывается дифференциальным уравнением более высокого порядка. Синтез корректирующих устройств методом ЛАЧХ. Данный метод, использующий ЛАЧХ, на протяжении многих лет был наиболее популярным методом синтеза регуляторов. Он основан на знании желаемой ЛАЧХ разомкнутой САУ. ЛФЧХ при этом не рассматривается. Предполагается, что система не имеет неустойчивых нулей и полюсов, является минимально-фазовой и при известной ЛАЧХ фазовая характеристика определяется однозначно. Желаемой ЛАЧХ называется такая ЛАЧХ, которой соответствует система с требуемыми показателями качества (время регулирования 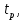 перерегулирование перерегулирование  , установившаяся ошибка). Задачей синтеза корректирующего устройства является выбор его структуры и параметров так, чтобы максимально приблизить ЛАЧХ скорректированной системы к желаемой. , установившаяся ошибка). Задачей синтеза корректирующего устройства является выбор его структуры и параметров так, чтобы максимально приблизить ЛАЧХ скорректированной системы к желаемой.Построение желаемой ЛАЧХ. При построении желаемой ЛАЧХ учитываются следующие требования, предъявляемые к системе: -время регулирования tp, -перерегулирование , -установившееся значение регулируемой величины, -порядок астатизма скорректированной системы r. Передаточную функцию разомкнутой исходной нескорректированной системы обозначим как 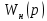 . .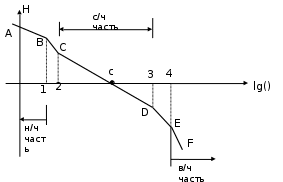 При построении желаемой ЛАЧХ в первом приближении будем считать, что она может быть заменена асимптотами. В ЛАЧХ условно можно выделить низкочастотную, среднечастотную и высокочастотную части (см. рис. 6.) Рис.6 Здесь АВ - низкочастотная, CD - среднечастотная, EF - высокочастотная части ЛАЧХ. Основные правила построения желаемой ЧХ. При построении желаемой ЛАЧХ в целях получения более простого корректирующего устройства необходимо учитывать ЛАЧХ уже имеющейся исходной системы. Поэтому перед построением желаемой ЛАЧХ строим ЛАЧХ, соответствующую передаточной функции 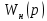 (располагаемую ЛАЧХ). (располагаемую ЛАЧХ).Основные правила построения желаемой ЛАЧХ заключаются в следующем: 1. Определяем значение коэффициента передачи разомкнутой скорректированной системы. Оно находится исходя из величины ошибки, возникающей из-за наличия задающего или возмущающего воздействия. Ошибка воспроизведения задающего воздействия а) статическая система, постоянное воздействие: 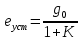 Если необходимо, чтобы было 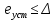 , ,то величина 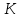 должна удовлетворять условию должна удовлетворять условию (4) (4) б) астатическая система, постоянное воздействие 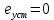 и  (5) (5)в) астатическая система, задающее воздействие 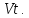 Тогда Тогда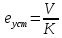 и, если 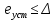 , то , то  (6) (6)г) гармоническое входное воздействие с амплитудой А и частотой  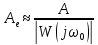 . .Если необходимо, чтобы Ае<, то ЛАЧХ скорректированной системы должна удовлетворять условию 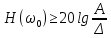 . .Ошибка, вызванная возмущающим воздействием, зависит от структурной схемы системы и места приложения воздействия. Однако всегда, в конечном итоге мы получаем условие  (7) (7)Где 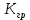 – некоторое граничное значение. С учетом полученных для конкретной системы условий (4) – (7) окончательно выбирается значение коэффициента передачи разомкнутой системы. – некоторое граничное значение. С учетом полученных для конкретной системы условий (4) – (7) окончательно выбирается значение коэффициента передачи разомкнутой системы.2. Строим низкочастотную асимптоту желаемой ЛАЧХ, исходя из выбранного значения 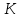 и заданного порядка астатизма разомкнутой системы и заданного порядка астатизма разомкнутой системы 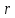 . Уравнение низкочастотной асимптоты желаемой ЛАЧХ имеет вид . Уравнение низкочастотной асимптоты желаемой ЛАЧХ имеет вид  т.е. низкочастотная асимптота имеет наклон  дб/дек. дб/дек.Высокочастотная часть должна совпадать с высокочастотной частью ЛАЧХ, соответствующей передаточной функции исходной системы 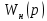 или проходить параллельно ей (см. рис. 7). Это обеспечивает максимальную простоту реализации корректирующего устройства. или проходить параллельно ей (см. рис. 7). Это обеспечивает максимальную простоту реализации корректирующего устройства.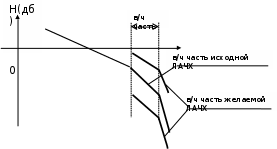 Рис.7. 3. Строим среднечастотную часть желаемой ЛАЧХ. Асимптота в области средних частот строится под наклоном (-20) дБ / дек через частоту среза которая определяется по заданным показателям качества tp,σ%, из таблицы
Частота 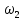 , ограничивающая область средних частот желаемой ЛАЧХ слева от частоты среза определяется значением отрезка L1, которая определяется в зависимости от заданной величины σmax из таблицы. Частота , ограничивающая область средних частот желаемой ЛАЧХ слева от частоты среза определяется значением отрезка L1, которая определяется в зависимости от заданной величины σmax из таблицы. Частота 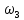 , которая ограничивает, область средних частот справа от частоты среза, определяется величиной отрезка L2 из условия |L2| ≥ L1. , которая ограничивает, область средних частот справа от частоты среза, определяется величиной отрезка L2 из условия |L2| ≥ L1. 4. Соединяем низкочастотную и среднечастотную асимптоты отрезками с наклонами, кратными 20 дб/дек. Обычно наклон отрезка, соединяющего низкочастотную и среднечастотную асимптоты, не превышает – 40 дб/дек. Если наклон получается больше – 40 дб/дек, то сопряжение проводят несколькими отрезками так, чтобы разница между наклонами соседних отрезков не превышала 20 дб/дек 5. Сопрягаем среднечастотную и высокочастотную части желаемой ЛАЧХ При этом предполагается, что при каждом значении изломе наклон ЛАЧХ изменяется на – 20 дб/дек. Пример. Построить желаемую ЛАЧХ системы. Передаточная функция исходной разомкнутой САУ имеет вид 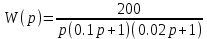 . .Требования к скорректированной системе следующие: Время переходного процесса 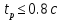 Перерегулирование 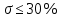 Порядок астатизма r=1. Построение желаемой ЛАЧХ выполняется в следующем порядке. Строится ЛАЧХ неизменяемой части системы (располагаемая ЛАЧХ), так как требования по точности специально не оговариваются, то коэффициент передачи разомкнутой системы при этом остается неизменным. Построенная ЛАЧХ показана на рис.8. 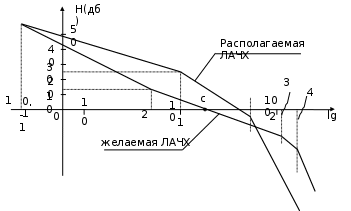 Рис.8 Выбираем частоту среза желаемой ЛАЧХ. Из таблицы по значению =30% найдем  , ,откуда 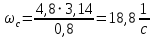 Примем с=19 [1/с]. Сопрягаем низкочастотную и среднечастотные асимптоты отрезков с наклоном –40 дб/дек. Правый конец сопрягающего отрезка помещаем в точку (0,63;13дб) желаемой ЛАЧХ, при этом 2=4,25 [1/с]. при этом условие 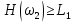 выполняется. Левую частоту сопряжения 1 определяем как точку пересечения отрезка с низкочастотной асимптотой располагаемой ЛАЧХ, 1=0,12 [1/с]. выполняется. Левую частоту сопряжения 1 определяем как точку пересечения отрезка с низкочастотной асимптотой располагаемой ЛАЧХ, 1=0,12 [1/с].4 .Сопрягаем среднечастотную и высокочастотную асимптоты. За частоты сопряжения принимаем 3=120 [1/с] и 4=180 [1/с]. При этом на частоте 3 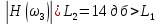 На этом построение желаемой ЛАЧХ закончено. Определение структуры и параметров корректирующего устройства. Пусть известна желаемая ЛАЧХ 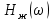 и задана передаточная функция разомкнутой нескорректированной системы Wн(р). Тогда и задана передаточная функция разомкнутой нескорректированной системы Wн(р). Тогда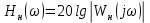 . .Рассмотрим случай, когда коррекция осуществляется последовательным корректирующим устройством с передаточной функцией Wк(p). Тогда ЛАЧХ скорректированной системы определяется как 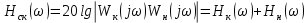 . .С другой стороны ЛАЧХ скорректированной системы должна быть равна желаемой ЛАЧХ, т.е. 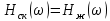 отсюда получим 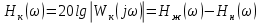 . .Таким образом, синтез последовательного корректирующего устройства осуществляют в следующем порядке: Строим асимптотическую ЛАЧХ нескорректированной системы (располагаемую ЛАЧХ) Строим желаемую ЛАЧХ скорректированной системы. Вычитая из желаемой ЛАЧХ располагаемую, получаем ЛАЧХ корректирующего устройства. Определяем передаточную функцию и подбираем схему и параметры корректирующего устройства. Проверяем, удовлетворяет ли скорректированная система предъявляемым к ней требованиям. На этом материал, выносимый на экзамен, заканчивается. Для желающих ниже помещается материал, посвященный еще одному способу синтеза – синтезу модального управления. В этом материале применяется самостоятельная нумерация формул. Модальное управление Поведение САУ определяется корнями характеристического уравнения. Каждому корню соответствует отдельная составляющая собстенного движения, называемая модой. Модальное управление – это управление, обеспечивающее требуемый характер переходных процессов за счет заданного распределения корней характеристического уравнения. Определение корней характеристического уравнения замкнутой САУ Корин должны находиться в области, определяемой требуемыми временм регулирования 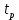 и перерегулированием и перерегулированием 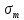 . Данная область определяется параметрами σ и μ. Имеем . Данная область определяется параметрами σ и μ. Имеем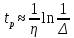 (η - степень устойчивости, Δ- величина «коридора», определяющего время регулирования) и тогда 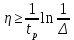 . (1) . (1)Для колебательности получим 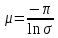 и 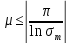 (2) (2)Дл\ систем 3-го и более высоких порядков к условиям (1), (2) должно быть добавлено требование достаточной удаленности вещественного корня от пары комплексно-сопряженных корней (в 3-5 раз по вещественным частям). Проведем формирование закона управления, обеспечивающего заданные корни характеристического уравнения на примере системы 3-его порядка.  Математическое описание объекта, полученное в результате поэлементного описания, имеет вид: 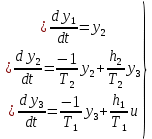 (3) (3)В матричной форме систему (3) можно представить в виде 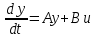 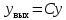 , (4) , (4)здесь y  , , 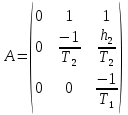 , , 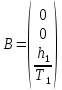 , , 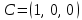 . .Передаточная функция объекта имеет вид 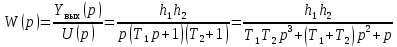 (5). (5). Выбор переменных состояния 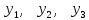 не является единственно возможным. Переменные состояния могут быть выбраны множеством способов. Любая замена вектора не является единственно возможным. Переменные состояния могут быть выбраны множеством способов. Любая замена вектора  на вектор на вектор 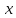 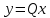 , (6) , (6)где 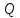 - неособая матрица ( - неособая матрица (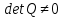 ) приводит к новому матричному уравнению ) приводит к новому матричному уравнению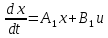 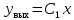 , (7) , (7) где 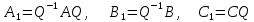 . (8) . (8)Выберем переменные состояния так, чтобы в системе (7) матрица 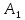 соответствовала системе дифференциальных уравнений, записанной в первой нормальной форме Коши, т.е., чтобы матрица соответствовала системе дифференциальных уравнений, записанной в первой нормальной форме Коши, т.е., чтобы матрица 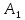 имела вид имела вид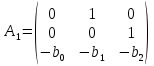 . (9) . (9)Для этого от передаточной функции (5) перейдем к дифференциальному уравнению объекта 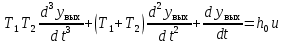 , , здесь 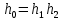 или или , (10) , (10) . Заметим, что характеристическое уравнение объекта, соответствующее передаточной функции (5) и дифференциальному уравнению (10), имеет вид . Заметим, что характеристическое уравнение объекта, соответствующее передаточной функции (5) и дифференциальному уравнению (10), имеет вид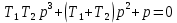 или 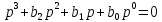 (здесь (здесь 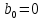 ). (11) ). (11)Выберем переменные состояния следующим образом:  . .При выбранных переменных система дифференциальных уравнений объекта примет вид 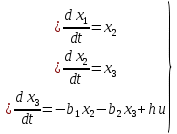 (12). (12).При этом матричное уравнение (7) имеет матрицы 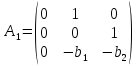 , , 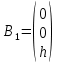 , , 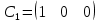 . .Сформируем управление 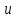 : :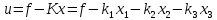 (13) (13)так, чтобы замкнутая система имела заранее заданные корни характеристического уравнения. Имеем для замкнутой системы 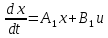 , , и тогда, исключая второе уравнение, получим матричное уравнение замкнутой системы 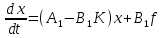 . .Рассмотрим собственную матрицу замкнутой системы 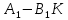 . Имеем . Имеем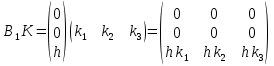 и тогда и тогда  . (14) . (14)Пусть желаемые корни (в общем случае комплексно-сопряженные) равны 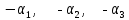 . Тогда по теореме Виета характеристическое уравнение может быть представлено в виде . Тогда по теореме Виета характеристическое уравнение может быть представлено в виде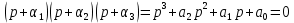 , (15) , (15)здесь 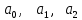 определяются по заданным значениям определяются по заданным значениям 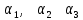 . Таким образом, необходимо, чтобы характеристическое уравнение замкнутой системы имело заданные коэффициенты. Рассмотрим вопрос, как связаны коэффициенты . Таким образом, необходимо, чтобы характеристическое уравнение замкнутой системы имело заданные коэффициенты. Рассмотрим вопрос, как связаны коэффициенты 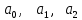 с элементами матрицы (14). Сравнивая вид матрицы с элементами матрицы (14). Сравнивая вид матрицы 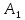 (9) с характеристическим уравнением (11), можно видеть, что элементы последней строки матрицы (9) с характеристическим уравнением (11), можно видеть, что элементы последней строки матрицы 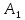 являются коэффициентами характеристического уравнения. в итоге получим являются коэффициентами характеристического уравнения. в итоге получим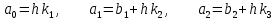 , , откуда значения коэффициентов, задающих требуемый закон управления определятся зависимостями 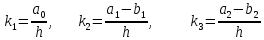 . (16) . (16)Зависимости (16) определяют коэффициенты обратных связей по переменным состояния в базисе 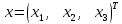 . Для окончательного решения задачи необходимо пересчитать эти коэффициенты для базиса . Для окончательного решения задачи необходимо пересчитать эти коэффициенты для базиса 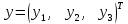 . .Имеем  , , 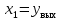 , ,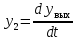 , , 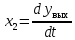 , ,откуда следует, что 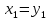 , , 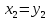 . (17) . (17)Для того, чтобы получить аналогичную зависимость для переменной 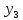 рассмотрим второе уравнение системы (3) рассмотрим второе уравнение системы (3) . . Приведем его к виду 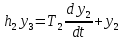 . (18) . (18)Так как 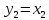 и, следовательно и, следовательно 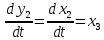 , , то из (18) получим 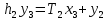 и  . (19) . (19)Подставляя (13), (19) в уравнение (13), получим 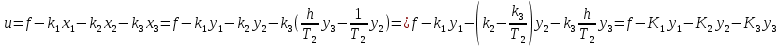 (20) (20) где 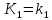 , , 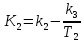 , , 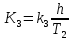 . .Рассмотрим теперь задачу в общей постановке. Уравнение объекта с одним входом имеет вид 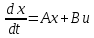 (21) (21)Здесь 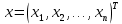 - вектор переменных состояния, - вектор переменных состояния, 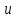 - скалярное управление, A= - скалярное управление, A=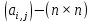 матрица, матрица, 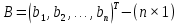 матрица. матрица.Сформируем управление 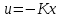 (22) (22)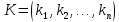 - матрица – строка коэффициентов так, чтобы замкнутая САУ имела желаемый характеристический многочлен - матрица – строка коэффициентов так, чтобы замкнутая САУ имела желаемый характеристический многочлен (23) (23)Решим задачу в два этапа. 1. Найдем строку коэффициентов для случая, когда матрицы 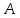 и и 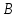 имеют вид имеют вид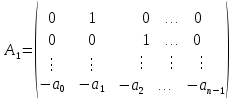 , ,  (24) (24)Уравнения состояния системы с матрицами вида (24) соответствуют канонической форме управляемости. 2. Покажем, как от системы (21) с произвольными матрицами 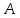 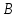 перейти к матрицам перейти к матрицам 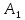 , , 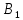 Итак, рассмотрим объект 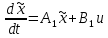 (25) (25)с матрицами 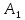 , , 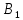 вида (24). вида (24). Уравнение (25) получено из (21) заменой переменных 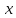 на на 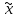 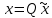  где - 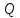 матрица перехода. матрица перехода.При этом 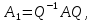 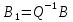 (26) (26)Заметим, что уравнение для определения собственных чисел матрицы 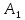 , т.е. корней характеристического уравнения САУ имеет вид , т.е. корней характеристического уравнения САУ имеет вид 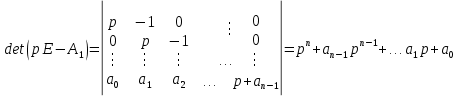 т.е. его коэффициенты образуют нижнюю строку матрицы 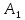 . .В новых переменных 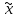 управление определяется как управление определяется как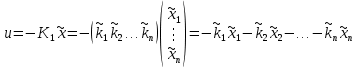 Уравнение замкнутой САУ имеет вид 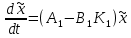 (27) (27) Здесь 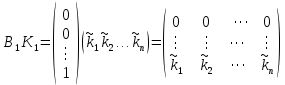 и тогда 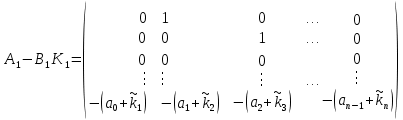 (28) (28)Характеристическое уравнение замкнутой САУ имеет вид 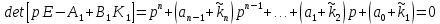 . (29) . (29)Нужно, чтобы это уравнение совпадало с желаемым характеристическим уравнением (23). Отсюда следует 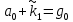 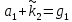 … 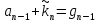 или 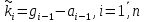 (30) (30)т.е. коэффициенты модального регулятора определяются как разность коэффициентов желаемого характеристического полинома замкнутой САУ и характеристического полинома объекта управления. Первый этап выполнен . Таким образом, в новой системе координат управление определяется зависимостью 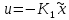 . .При возврате к прежней системе координат получим 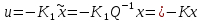 где 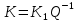 Остается найти матрицу перехода 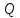 . Ранее имели . Ранее имели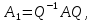 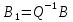 откуда 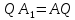 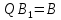 (31) (31)Матрица перехода 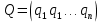 может быть последовательно вычислена по столбцам. Из второго из уравнений (31) имеем может быть последовательно вычислена по столбцам. Из второго из уравнений (31) имеем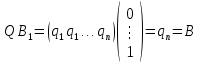 Из первого уравнения (31) имеем 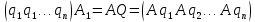 или 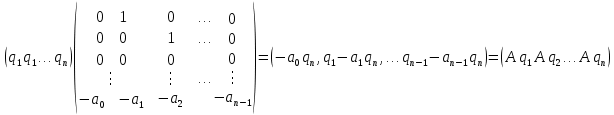 В итоге получим 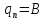 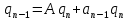 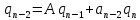 …  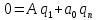 Последняя строка служит для контроля правильности вычислений. Для синтеза модального управления в Mathlab имеются соответствующие функции acker - для синтеза управления с одним входом и place - для синтеза, когда u является вектором. При использовании модального управления не требуется проверка на устойчивость, не требуются дополнительные корректирующие устройства, не повышается порядок системы. |