ТОР. Синтез сигналов по дискретныи отсчетам
 Скачать 5.8 Mb. Скачать 5.8 Mb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра ТОР отчет по лабораторной работе №8 по дисциплине «Теоретические основы радиотехники» Тема: СИНТЕЗ СИГНАЛОВ ПО ДИСКРЕТНЫИ ОТСЧЕТАМ
Санкт-Петербург 2022 Цель работы: изучение принципов дискретизации и восстановления сигналов на основе теоремы Котельникова. Теоретические материалы Для «идеального» ФНЧ с частотой среза fm = 11 кГц определить минимальную длительность прямоугольного импульса – такую, чтобы при его дискретизации и последующем восстановлении передавались все составляющие спектра с амплитудами, большими 0,1 от максимальной, т. е. 3 лепестка функции 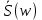 . .Если сигнал ограничен частотой fm, то он может быть взят без потери информации через интервал времени 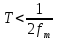 . . T – интервал дискретизации Tc – длительность сигнала N – число отсчётов 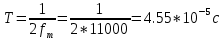 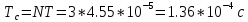 Определить частоту дискретизации, минимально необходимую при использовании фильтра, указанного в п. 1 ( fm = 11 кГц).  Изобразить синтезируемые сигналы и их дискретные отсчеты, следующие через 1/22 мс (45,45 мкс) и 1/44 мс (22,73 мкс): а) видеоимпульс прямоугольной формы с длительностью, рассчитанной в п.1; б) радиоимпульс прямоугольной формы с несущей частотой fср = 44 кГц и длительностью, рассчитанной в п.1; в) гармонический сигнал с частотой fср = 11 кГц. Построить спектр сигнала, указанного в п. 3а. Экспериментальные материалы Получить и зарисовать импульсную характеристику и модуль комплексного коэффициента передачи: а) для RC-фильтра 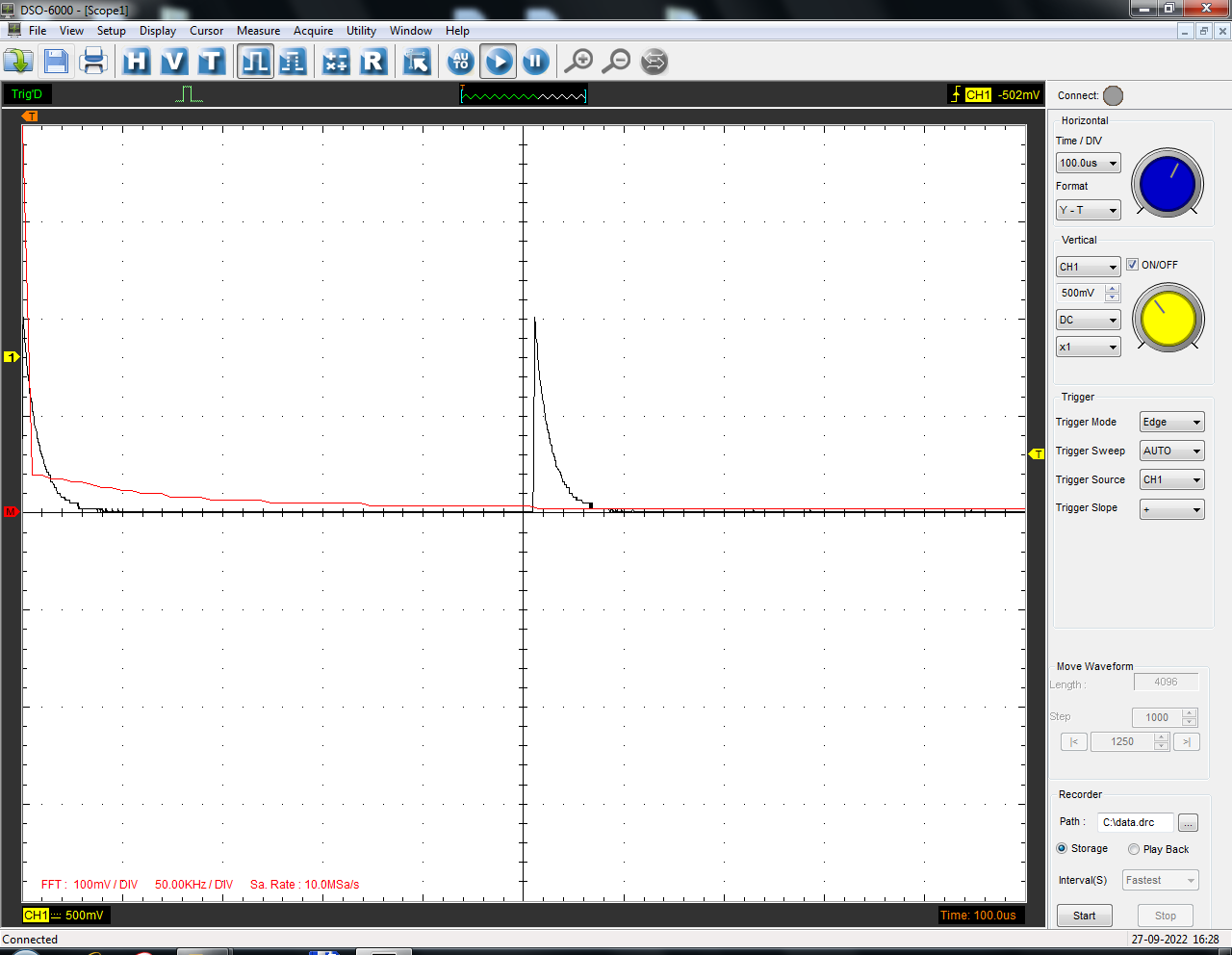 б) для ФНЧ 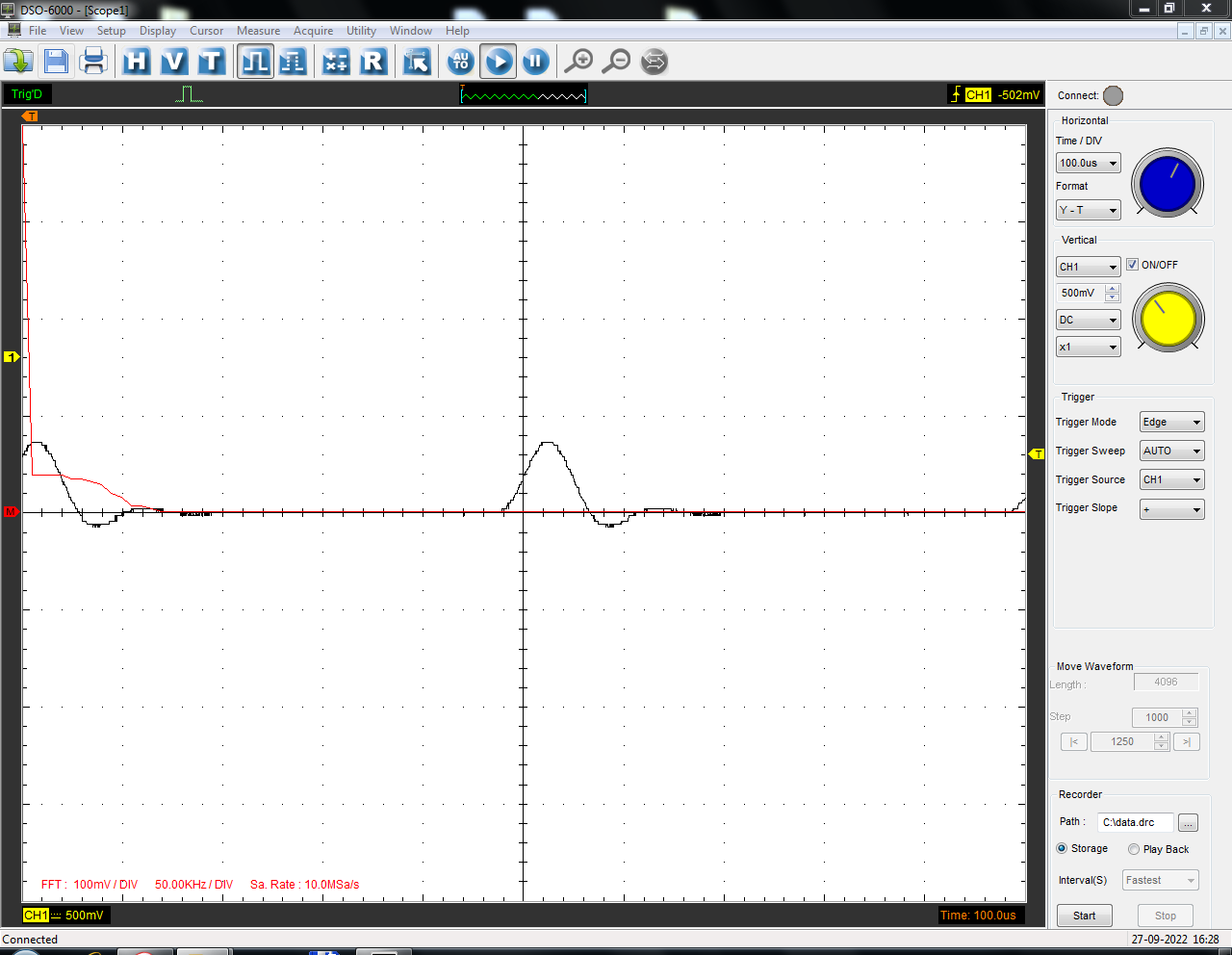 в) для ПФ 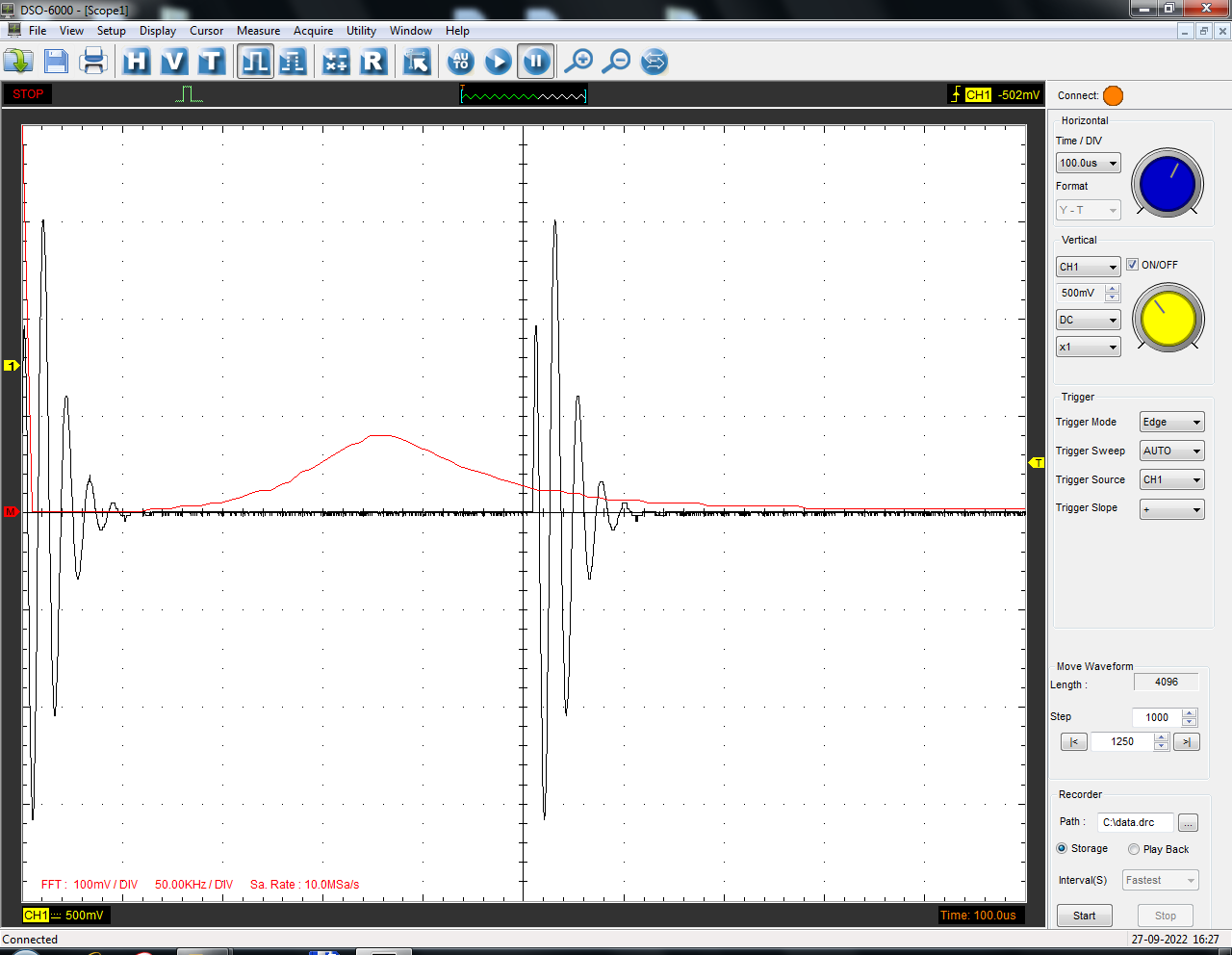 Получить и зарисовать осциллограммы и спектры дискретизированных сигналов для двух частот дискретизации – 22 и 44 кГц. 1-ый сигнал: 22 кГц: 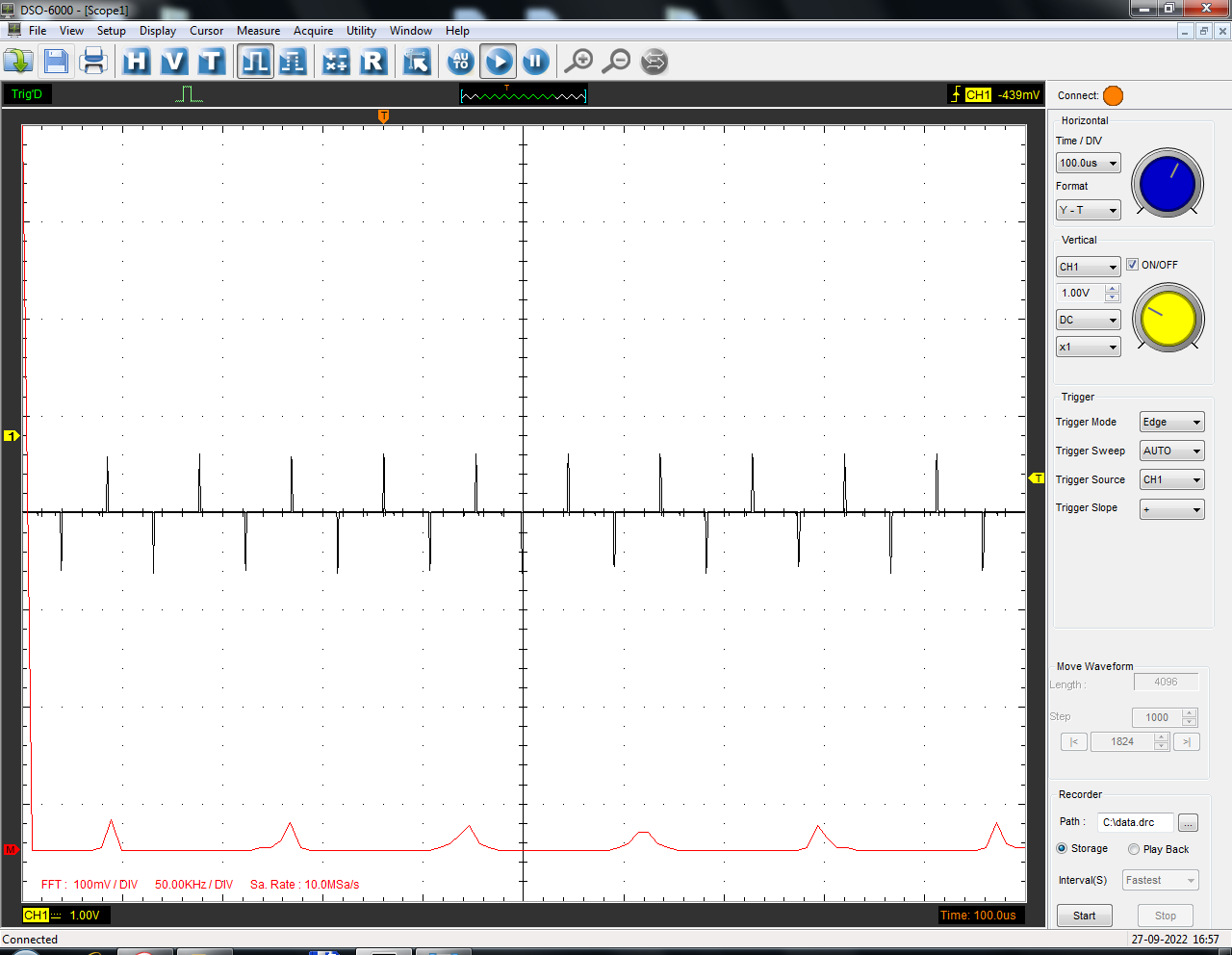 44 кГц: 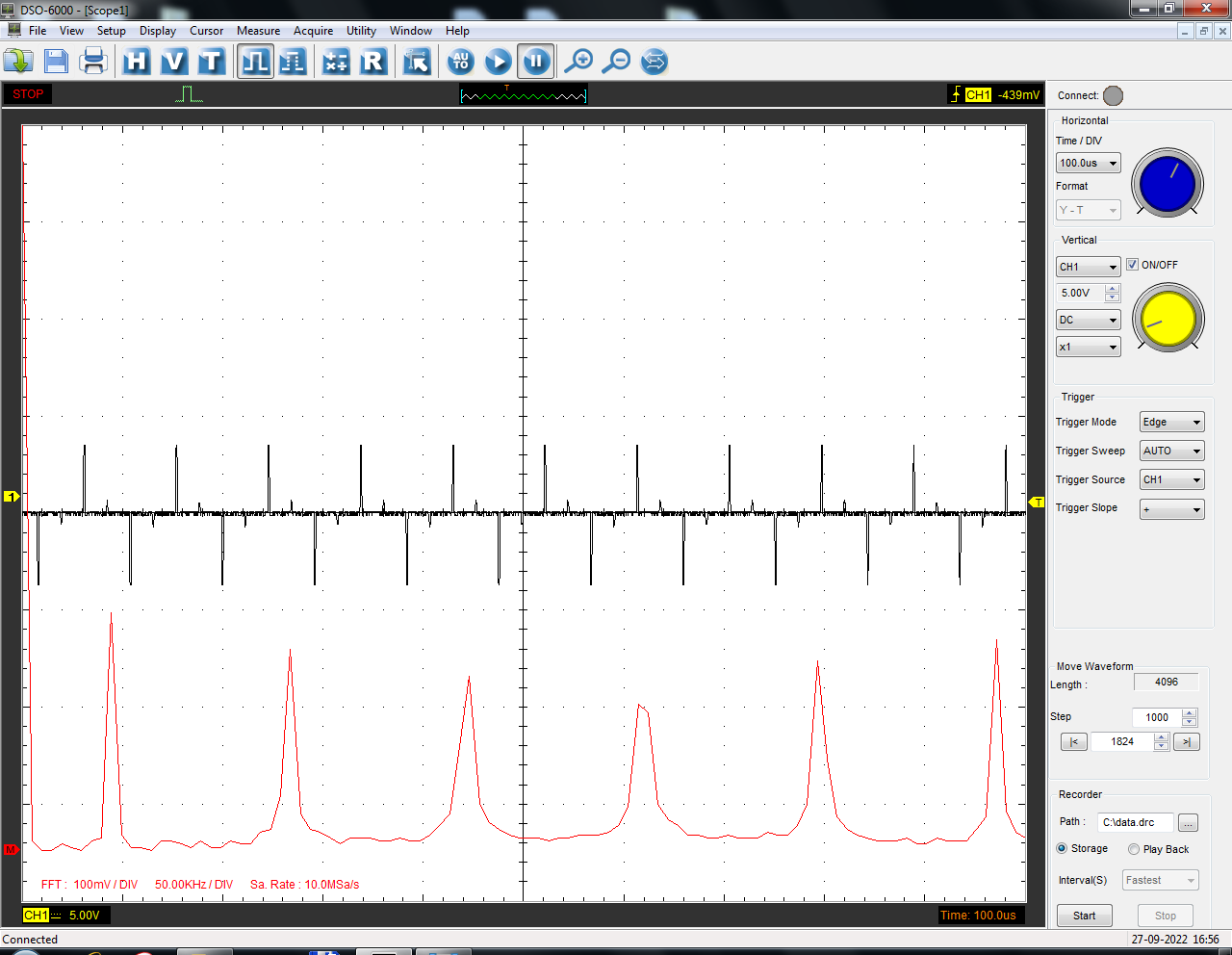 2-ой сигнал: 22 кГц: 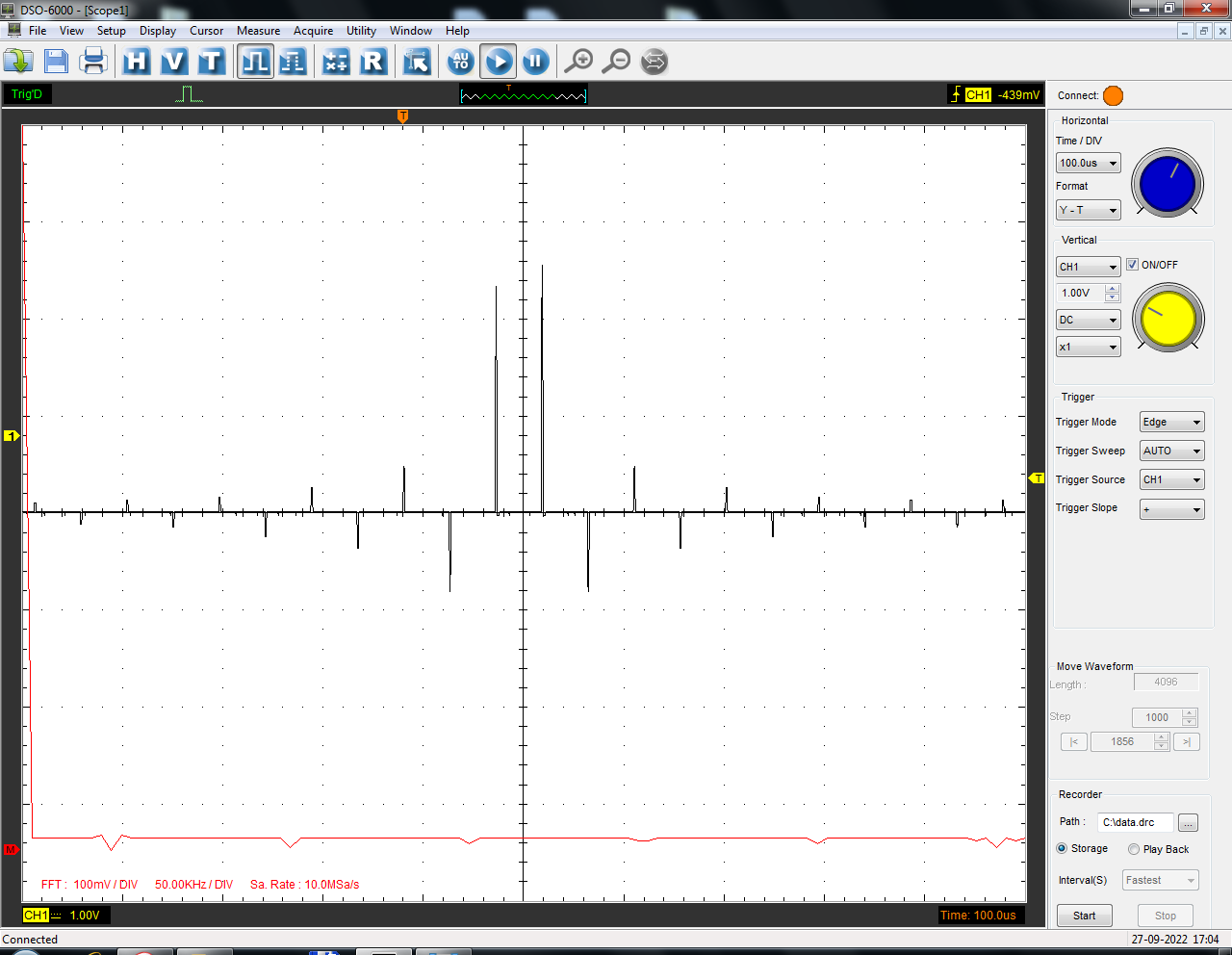 44 кГц 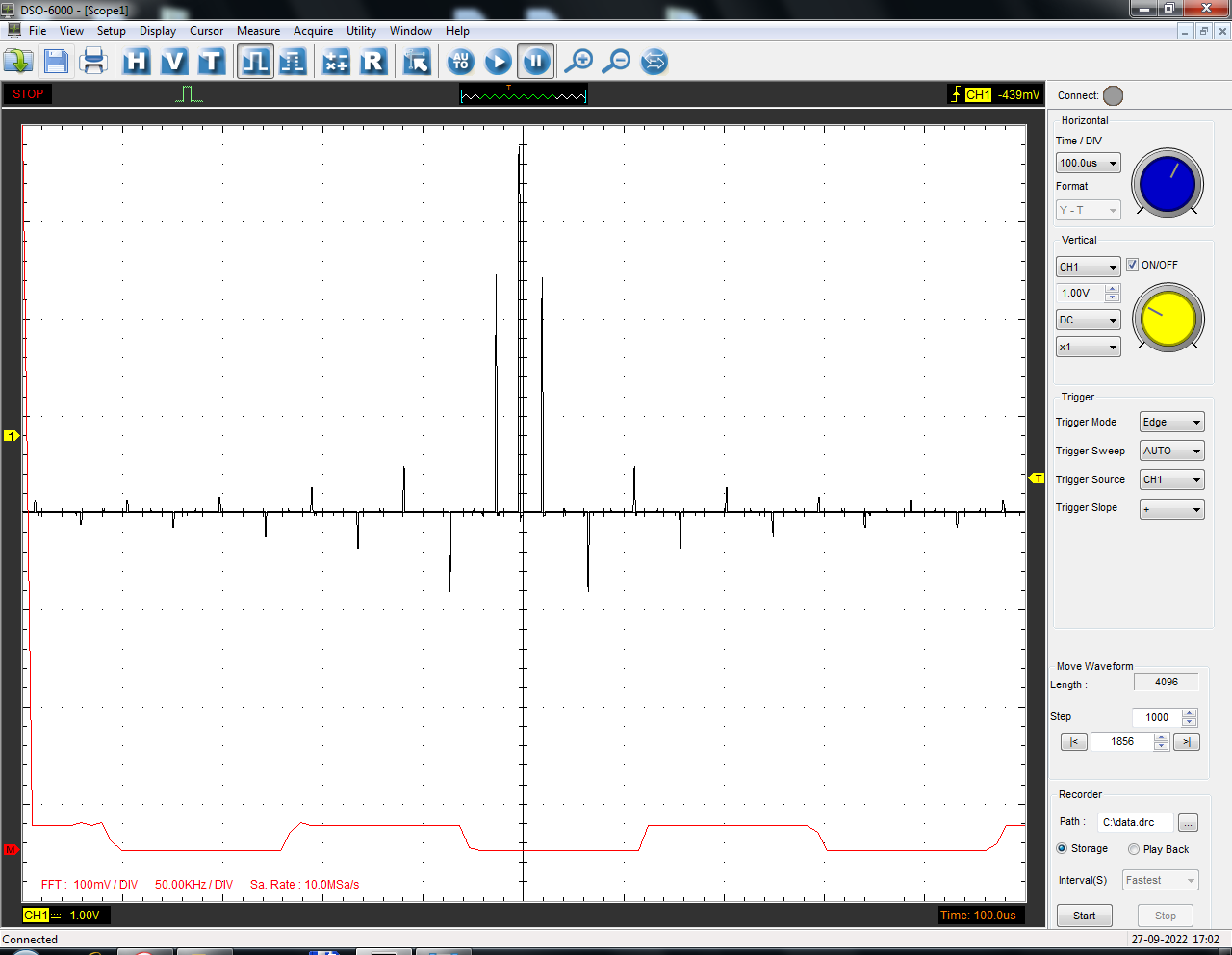 3-ий сигнал: 22 кГц 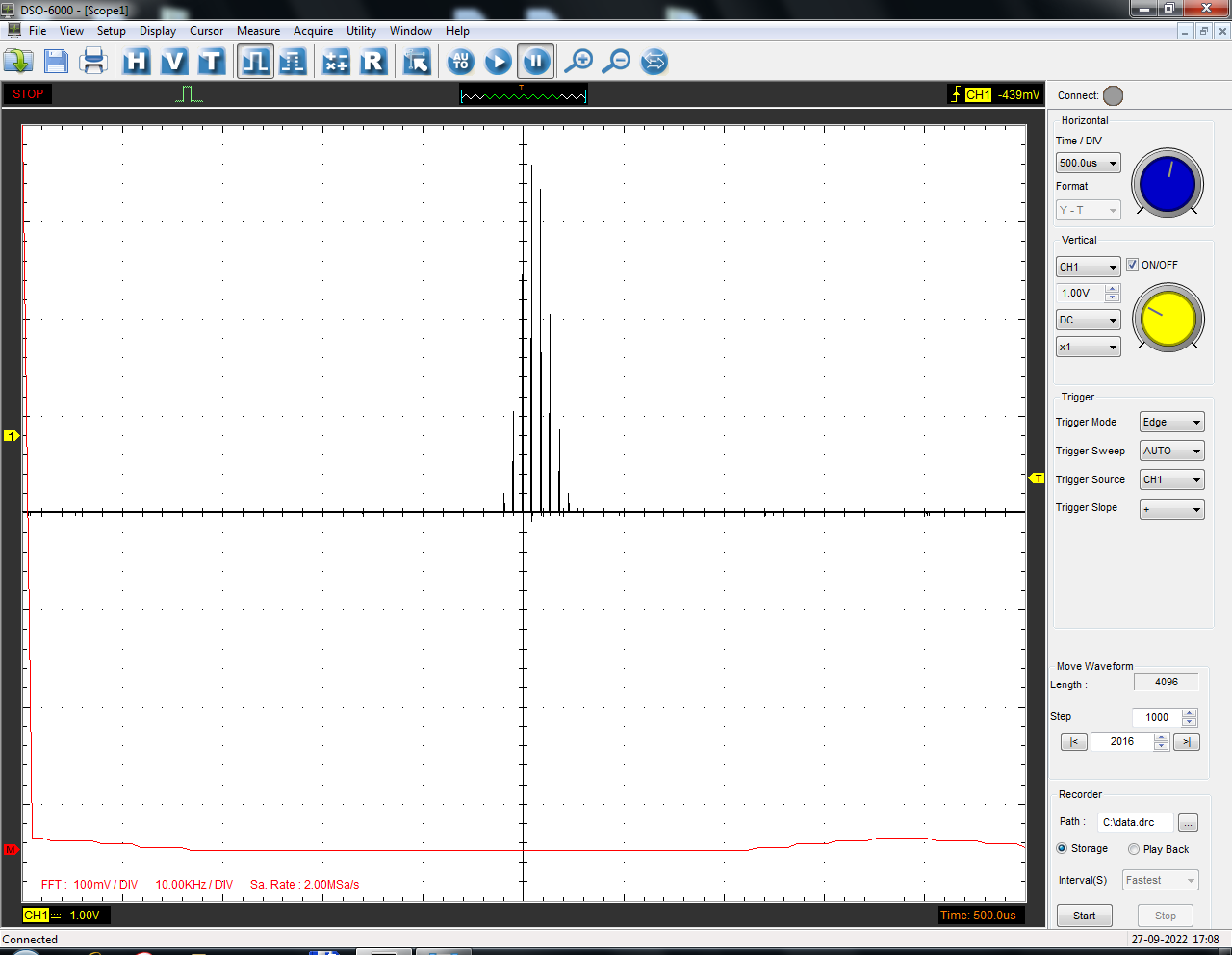 44 кГц: 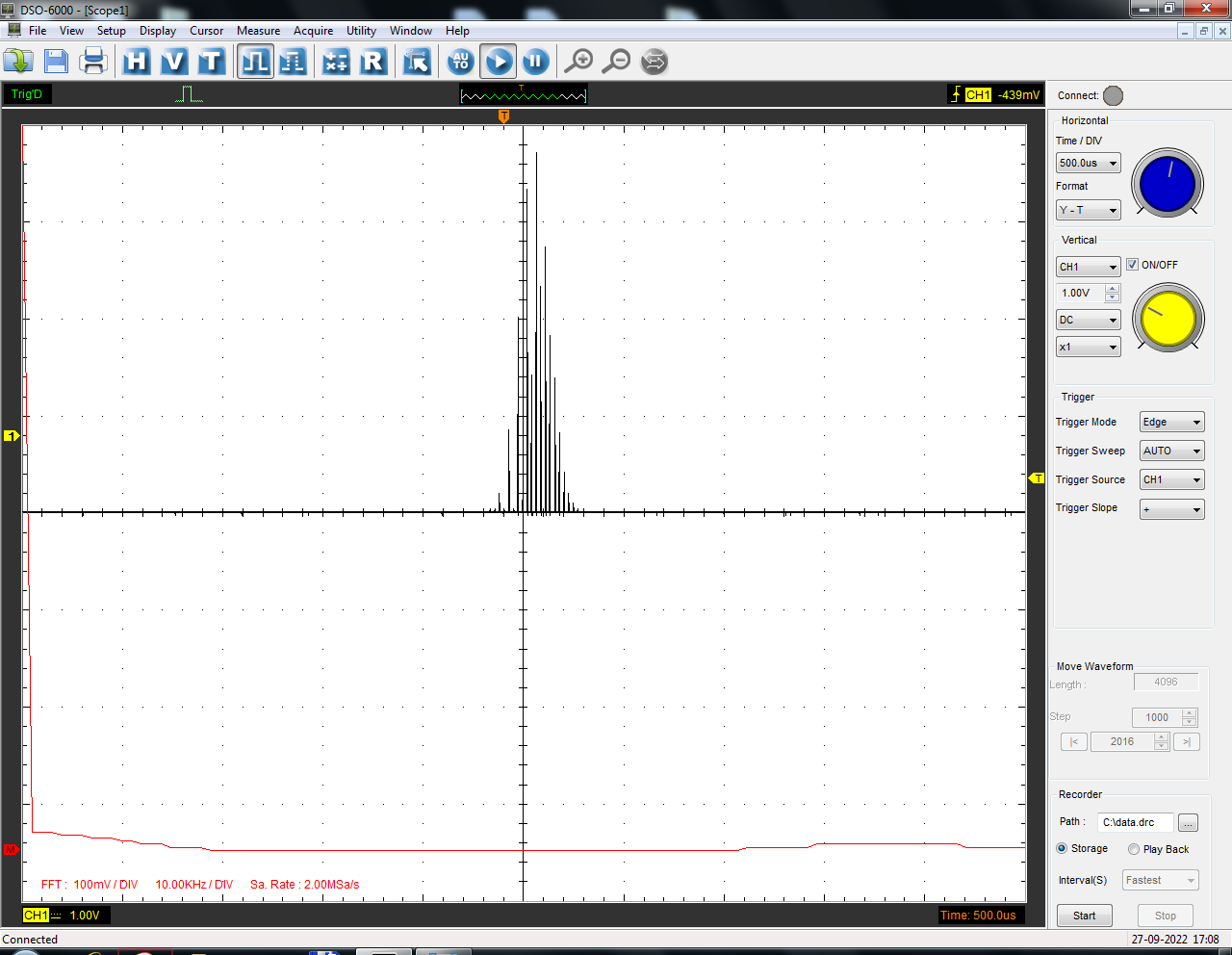 4-ый сигнал: 22 кГц 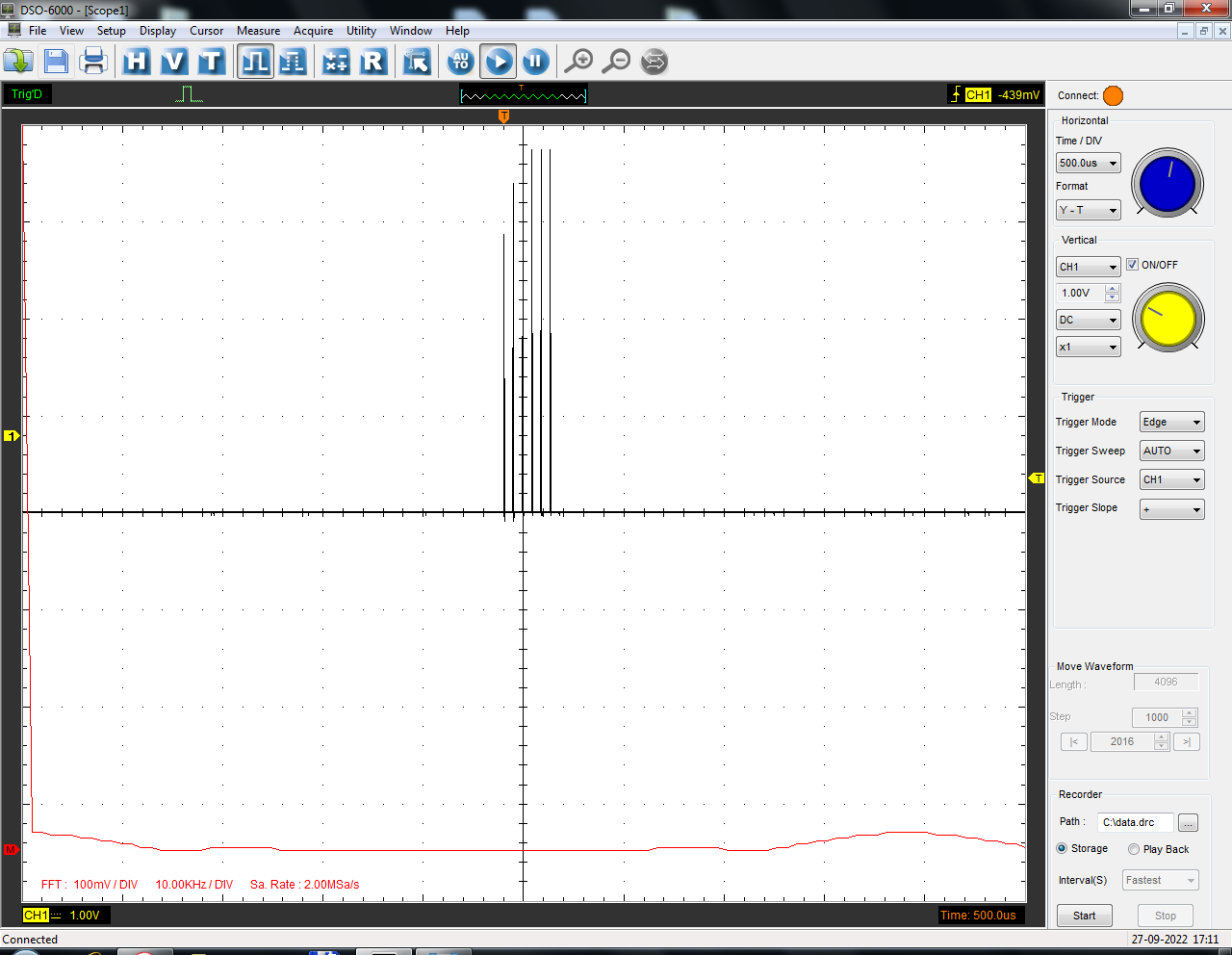 44 кГц 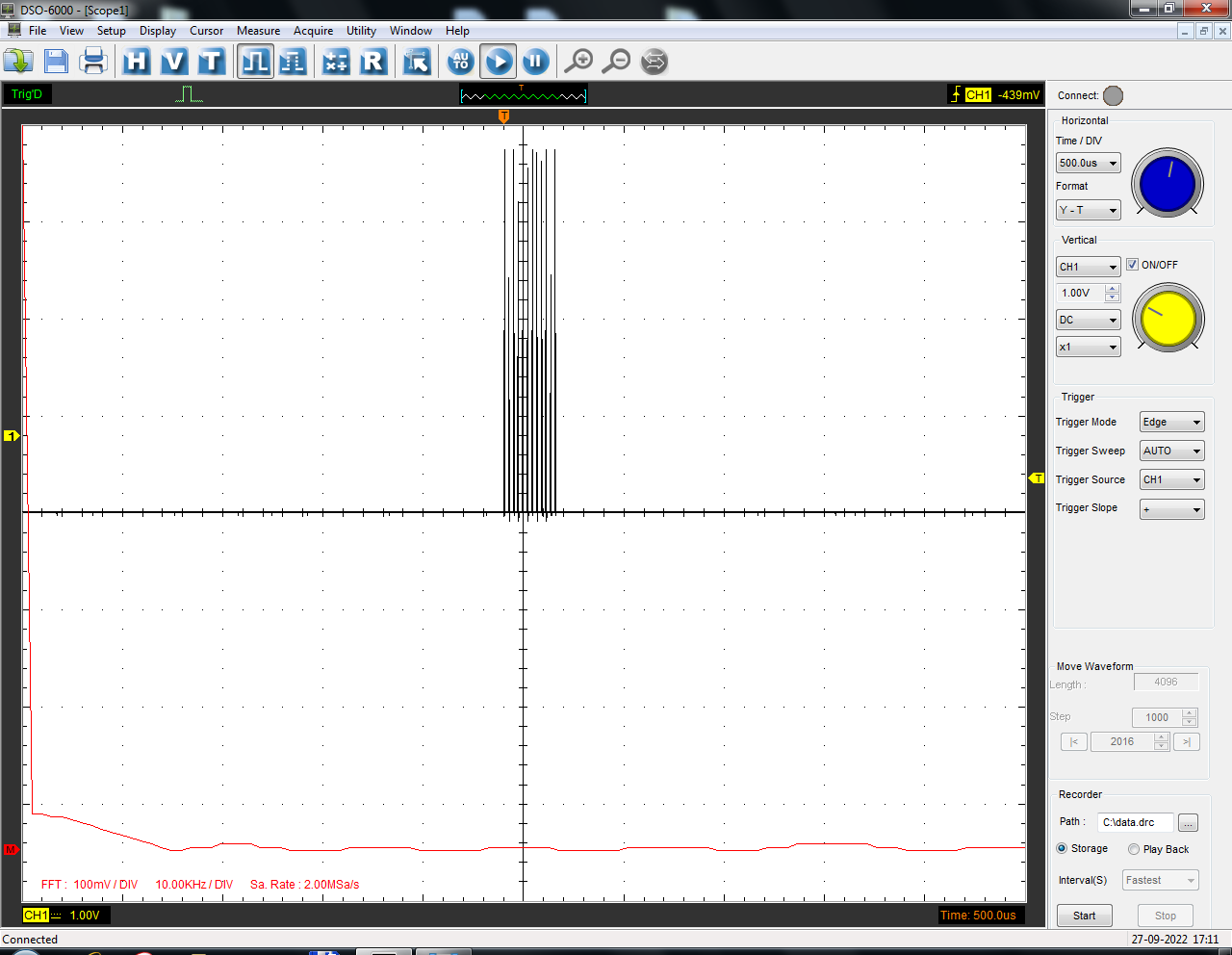 Получить и зарисовать осциллограммы и спектр восстановленных сигналов. Восстановление производить с помощью всех фильтров поочередно для двух частот дискретизации – 22 и 44 кГц. 1-ый сигнал: FN: 22 кГц: 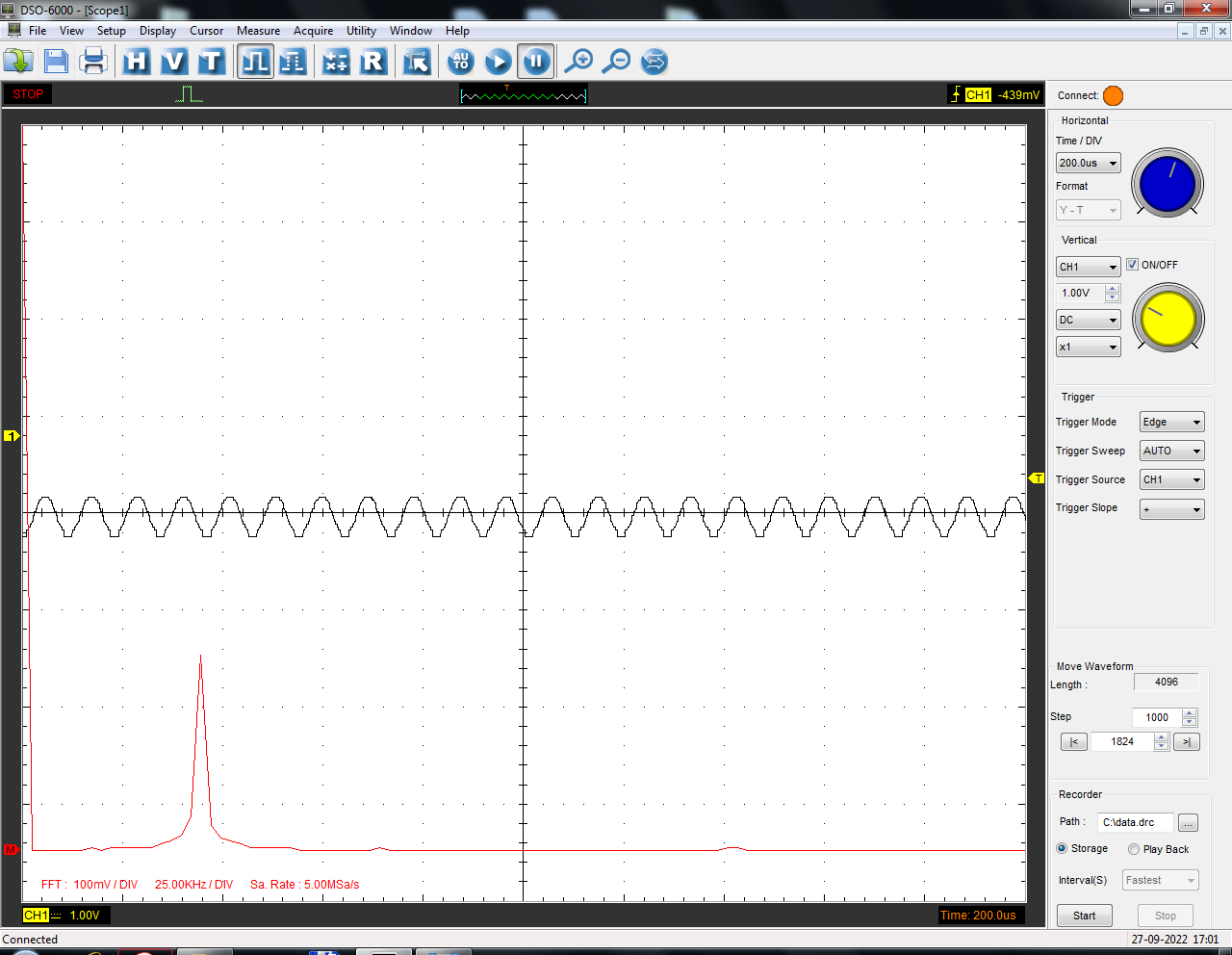 44 кГц: 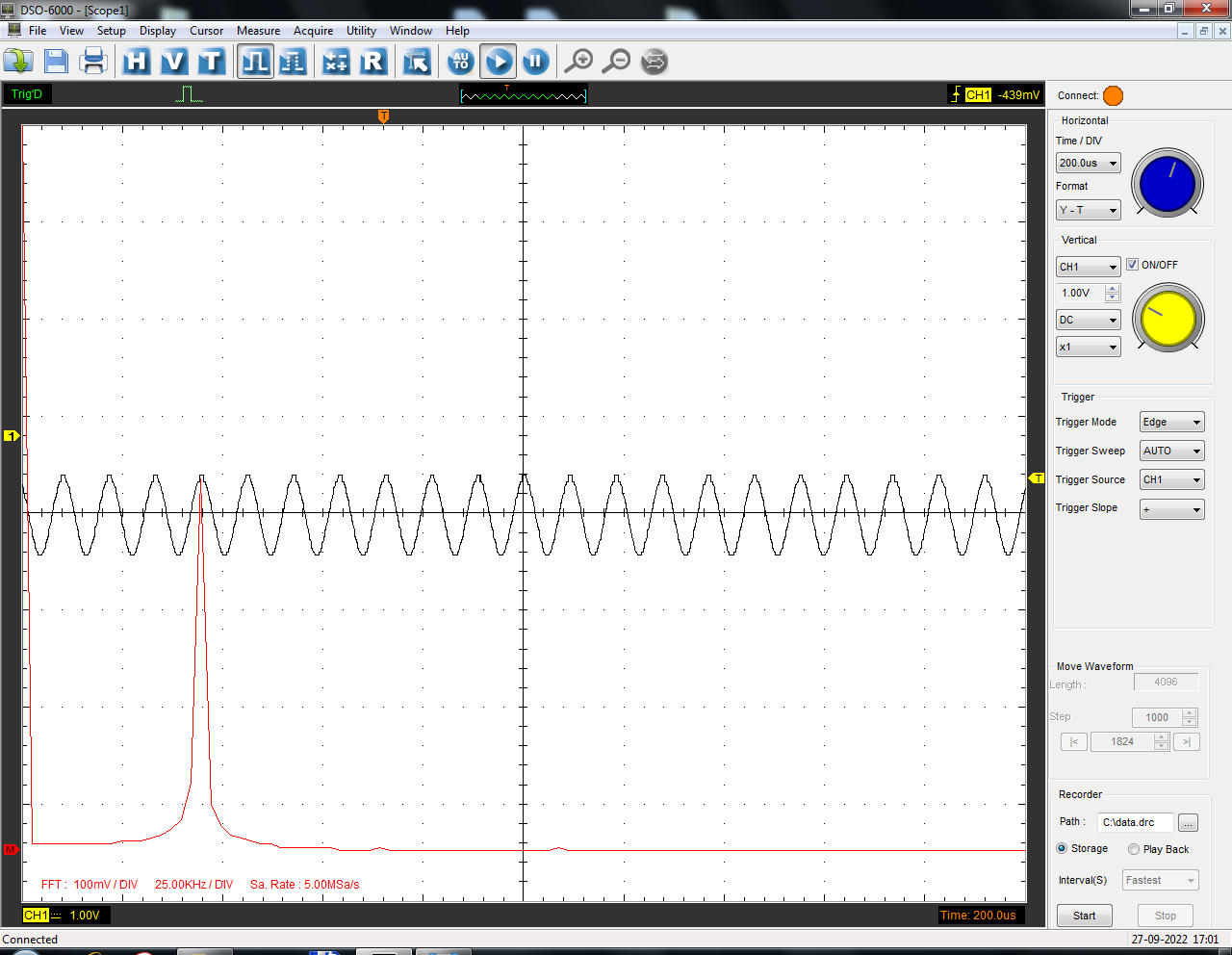 PF: 22 кГц: 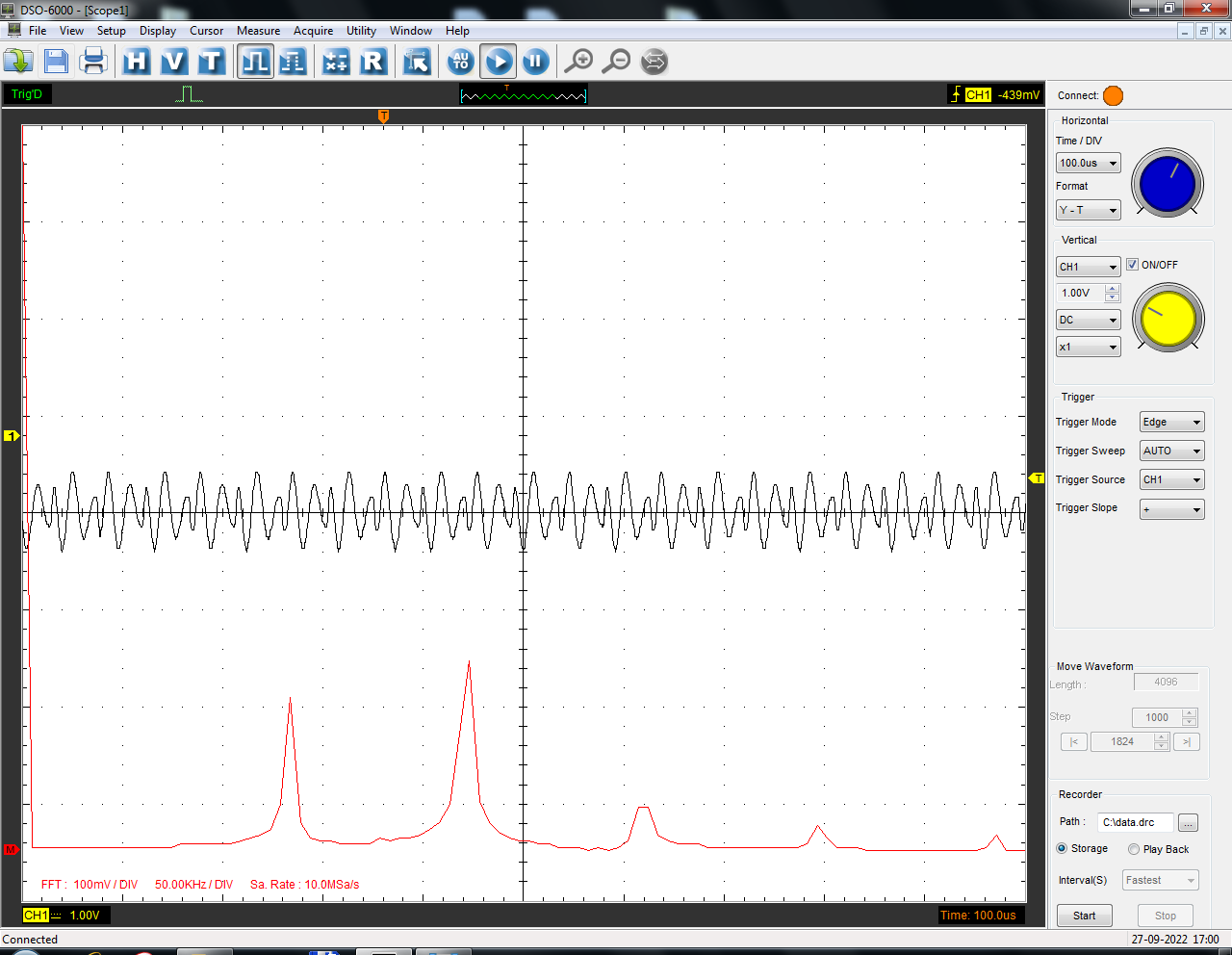 44 кГц: 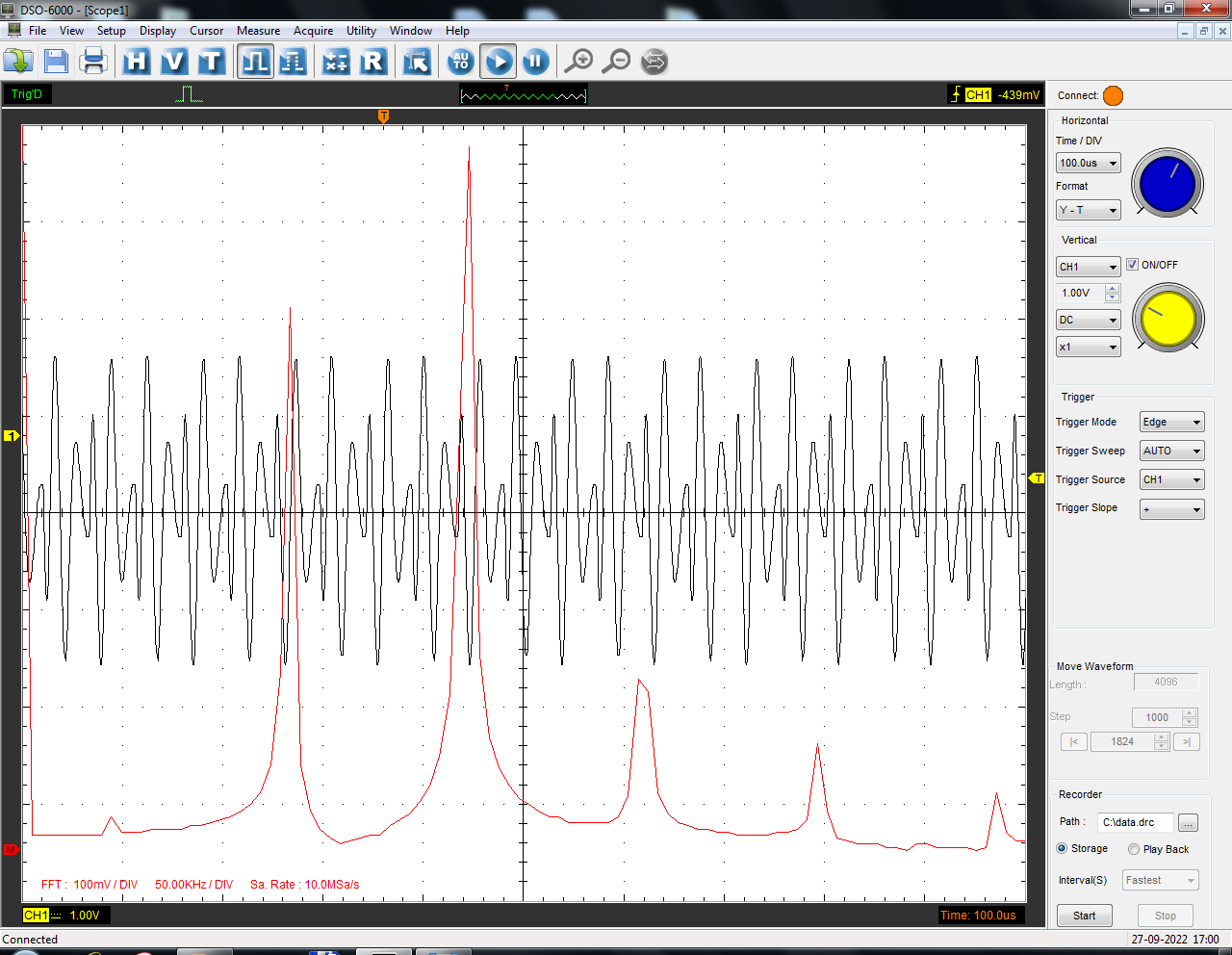 RC: 22 кГц: 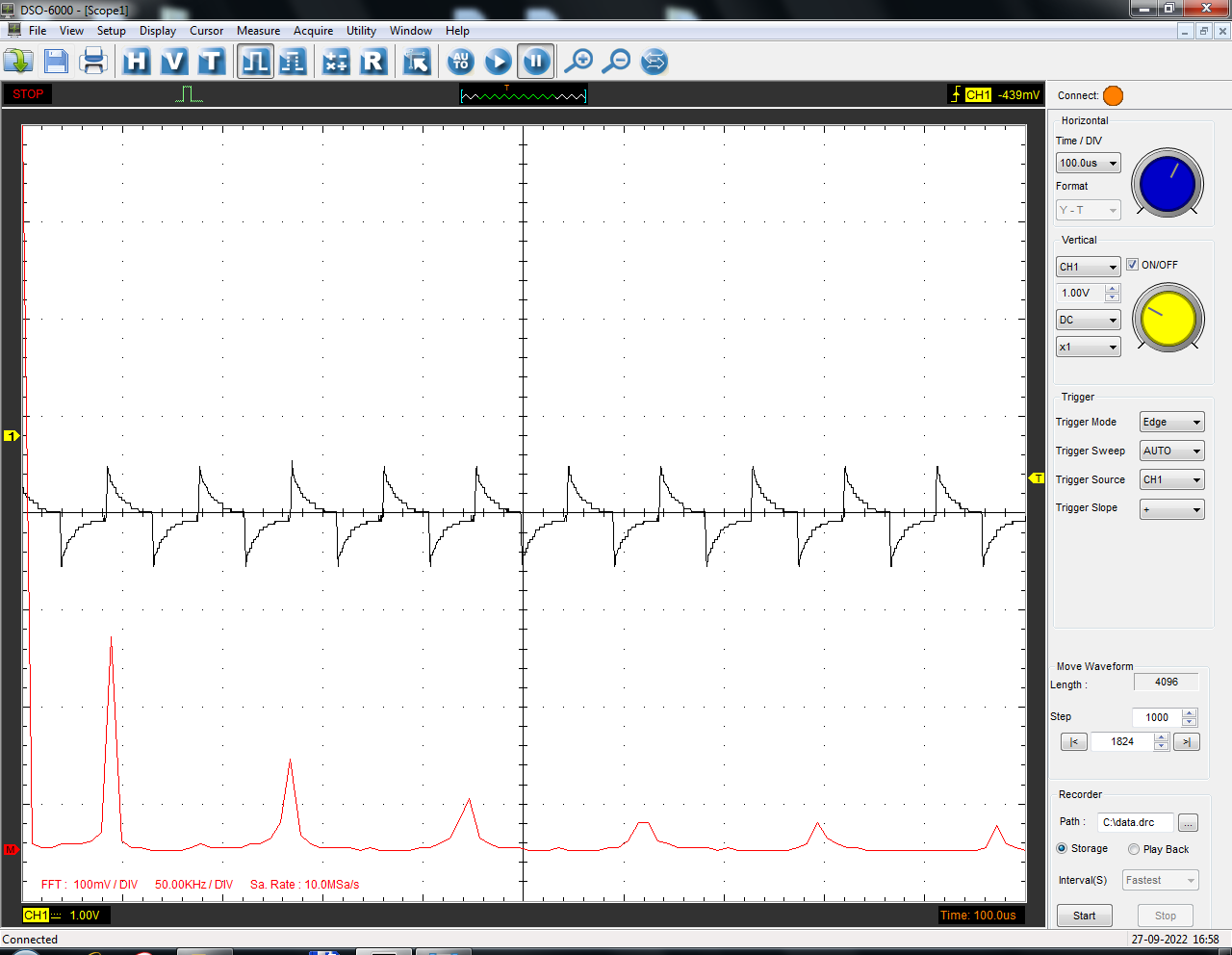 44 кГц: 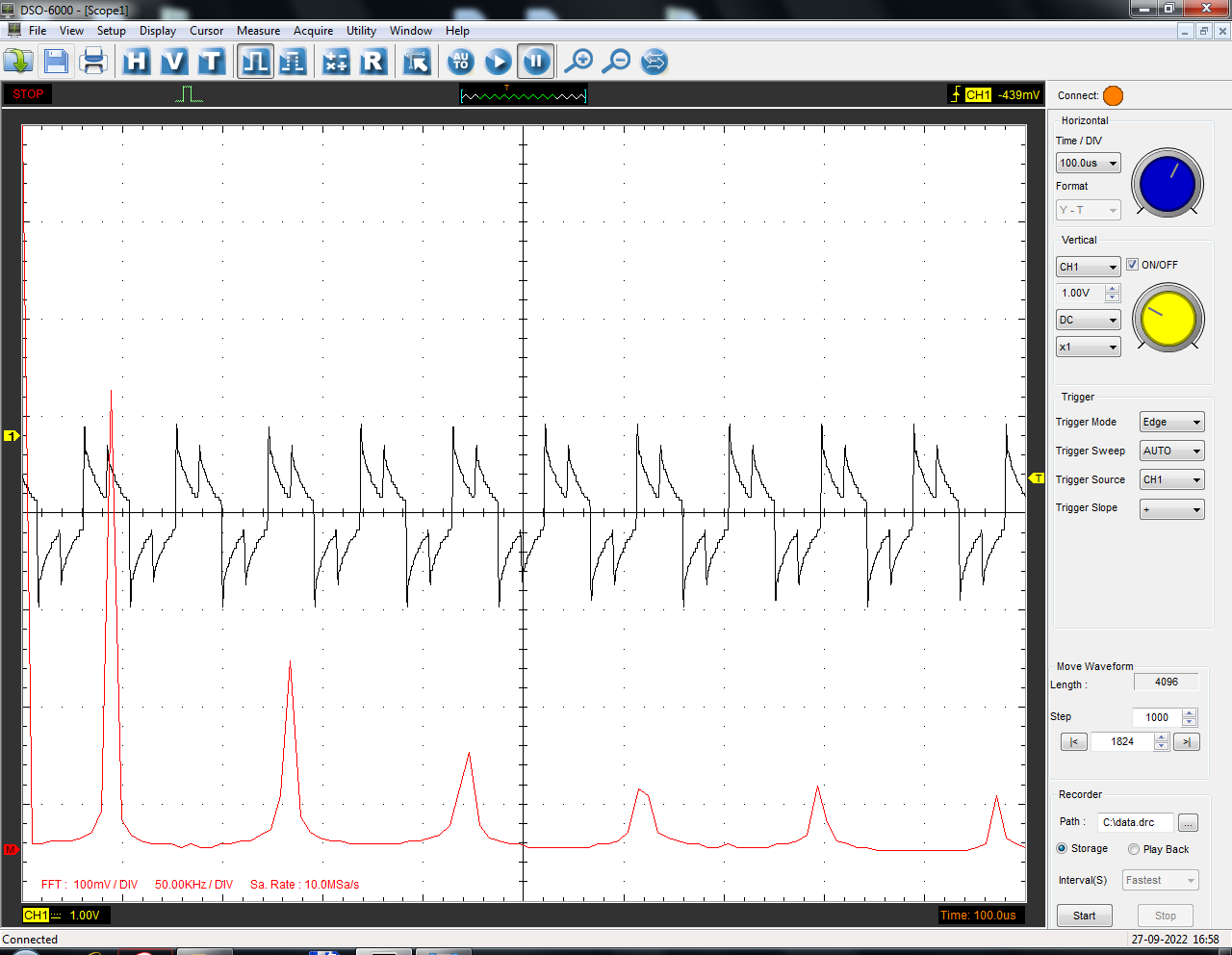 2-ой сигнал: FN: 22 кГц: 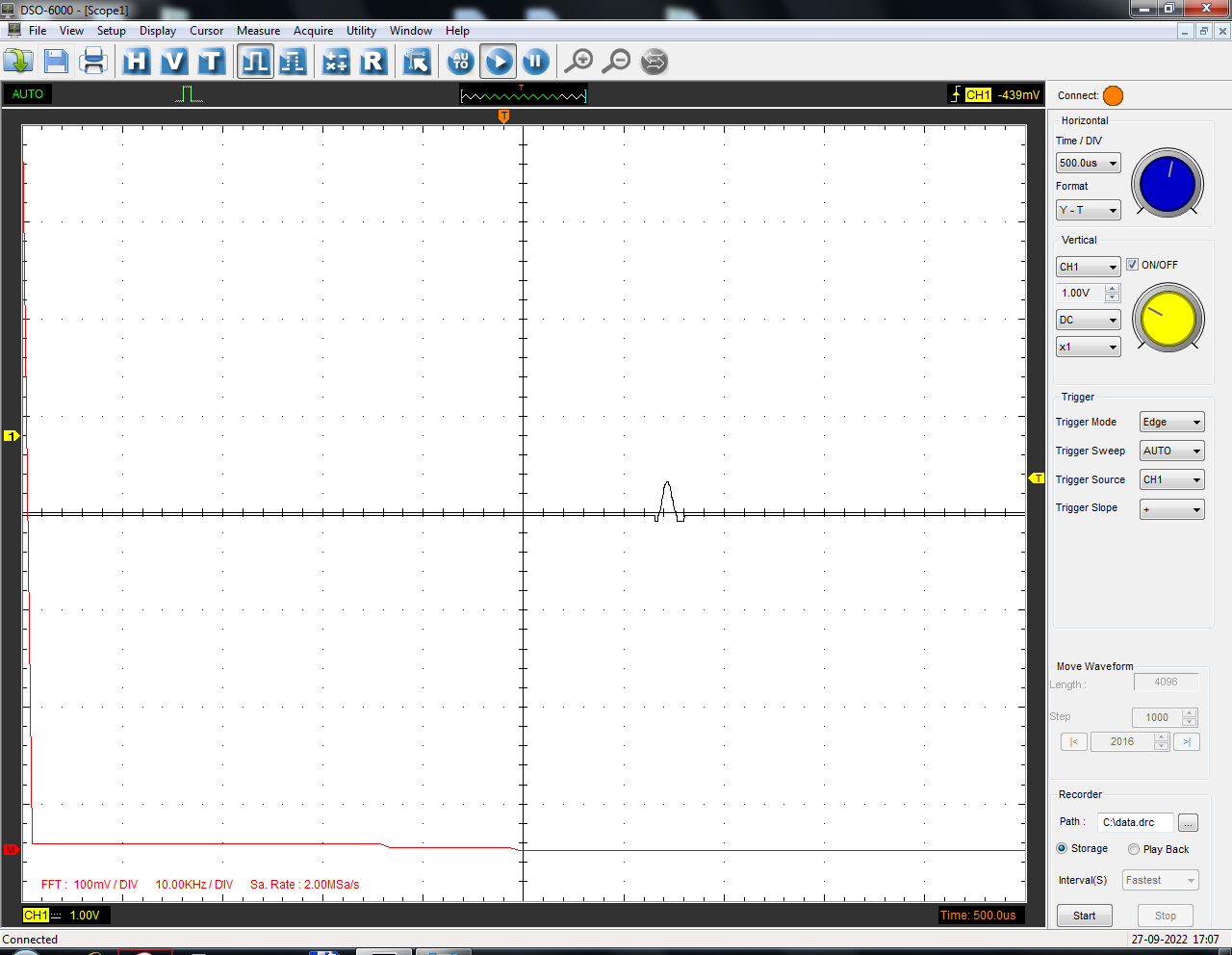 44 кГц: 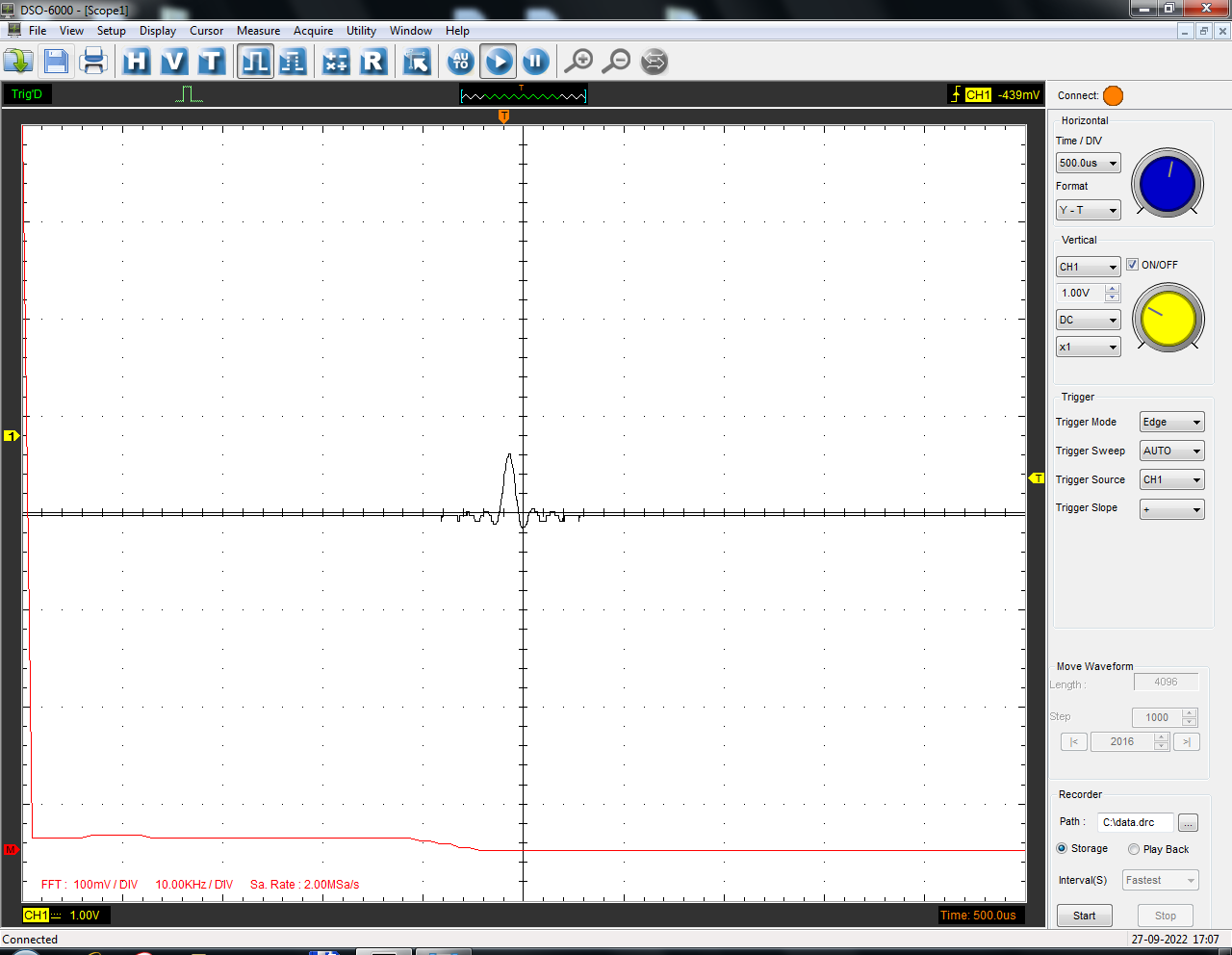 PF: 22 кГц: 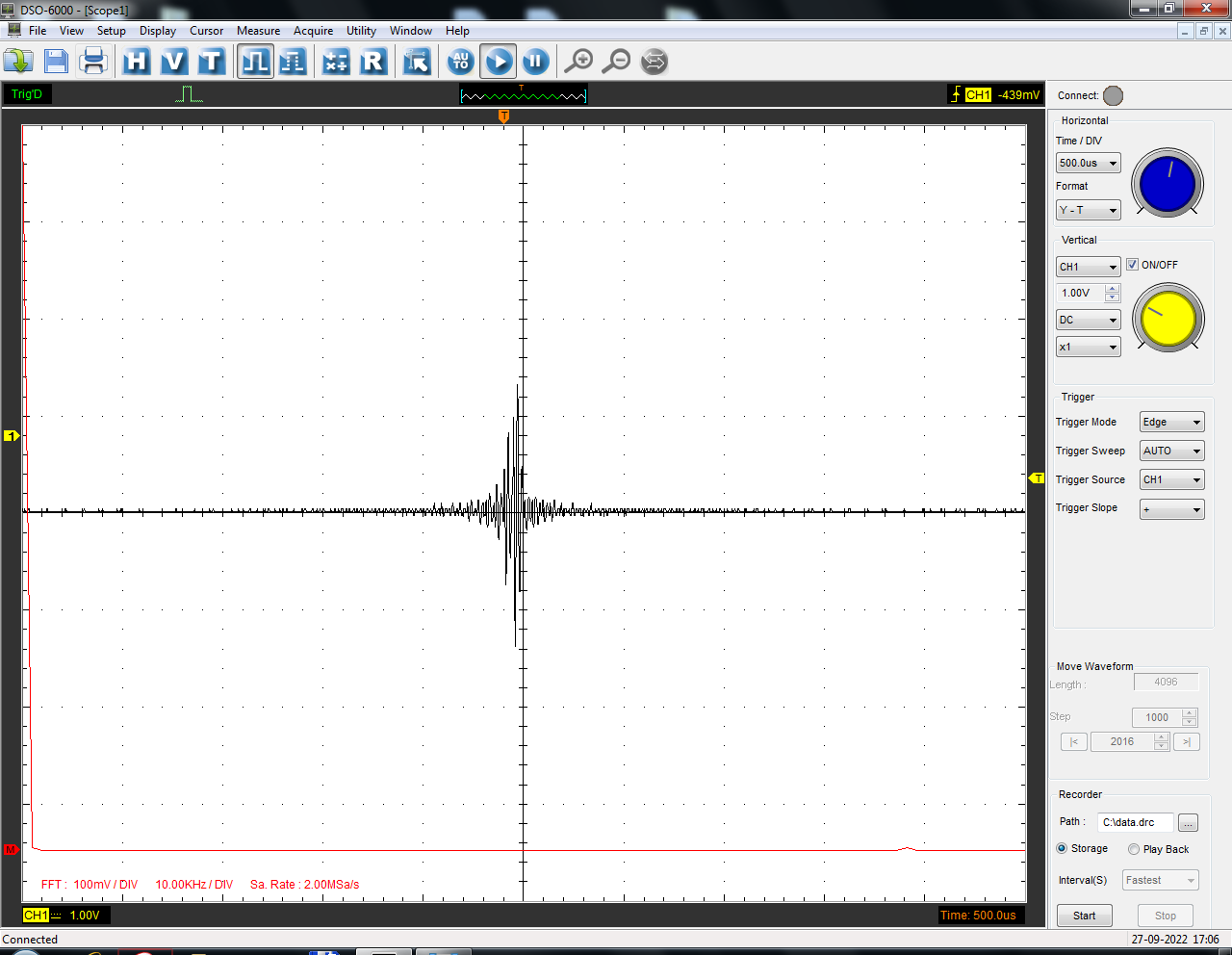 44 кГц: 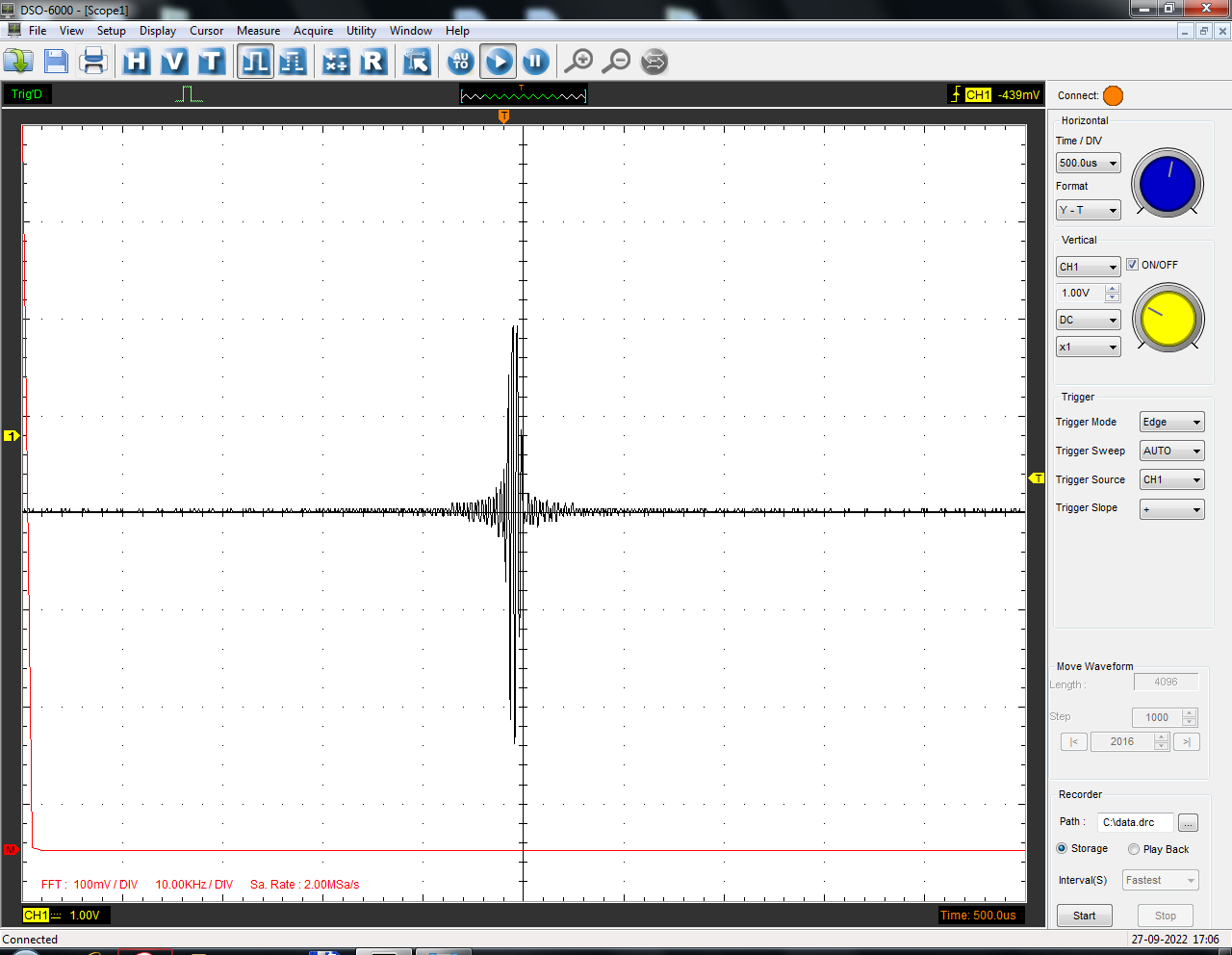 RC: 22 кГц: 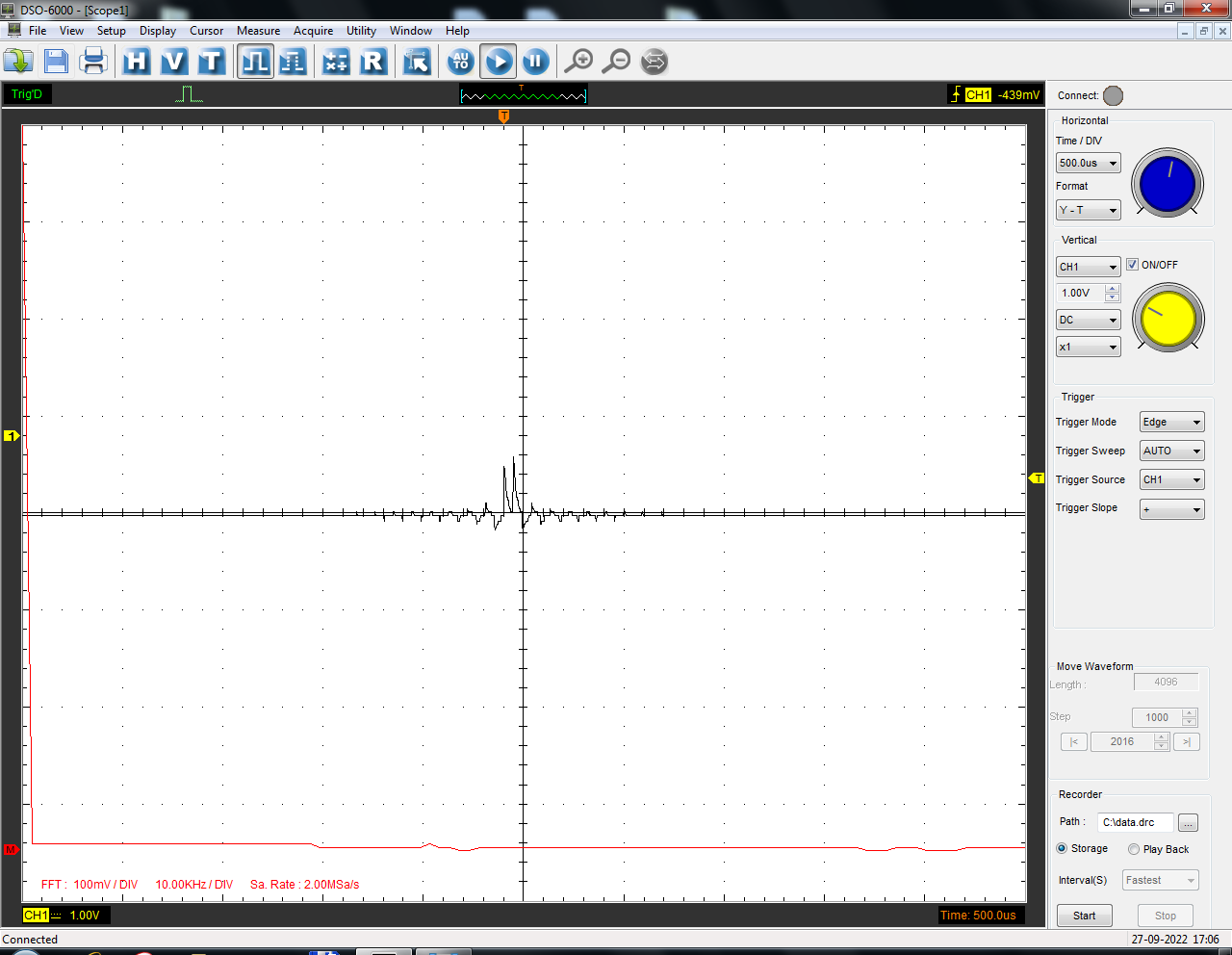 44 кГц: 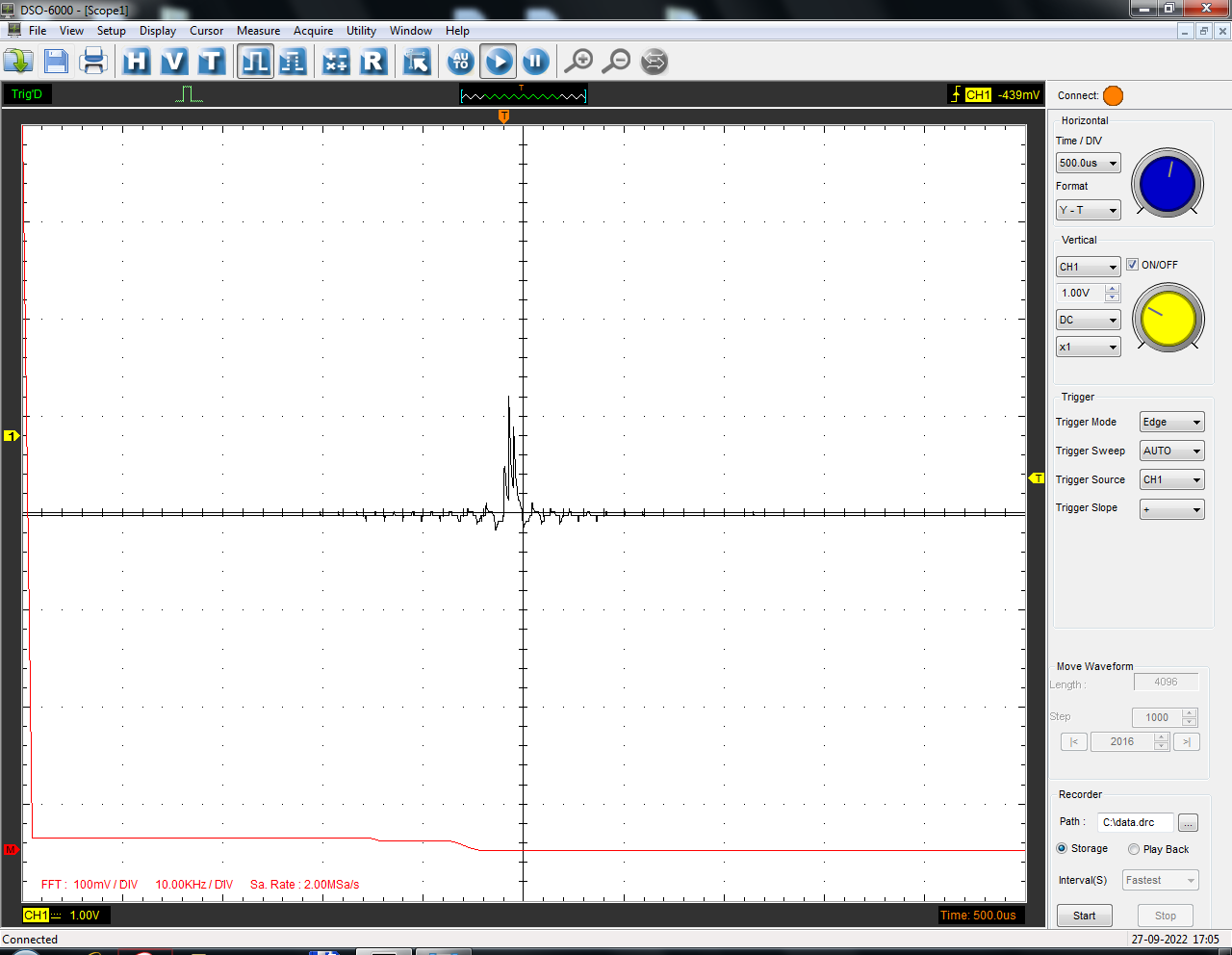 3-ий сигнал: FN: 22 кГц: 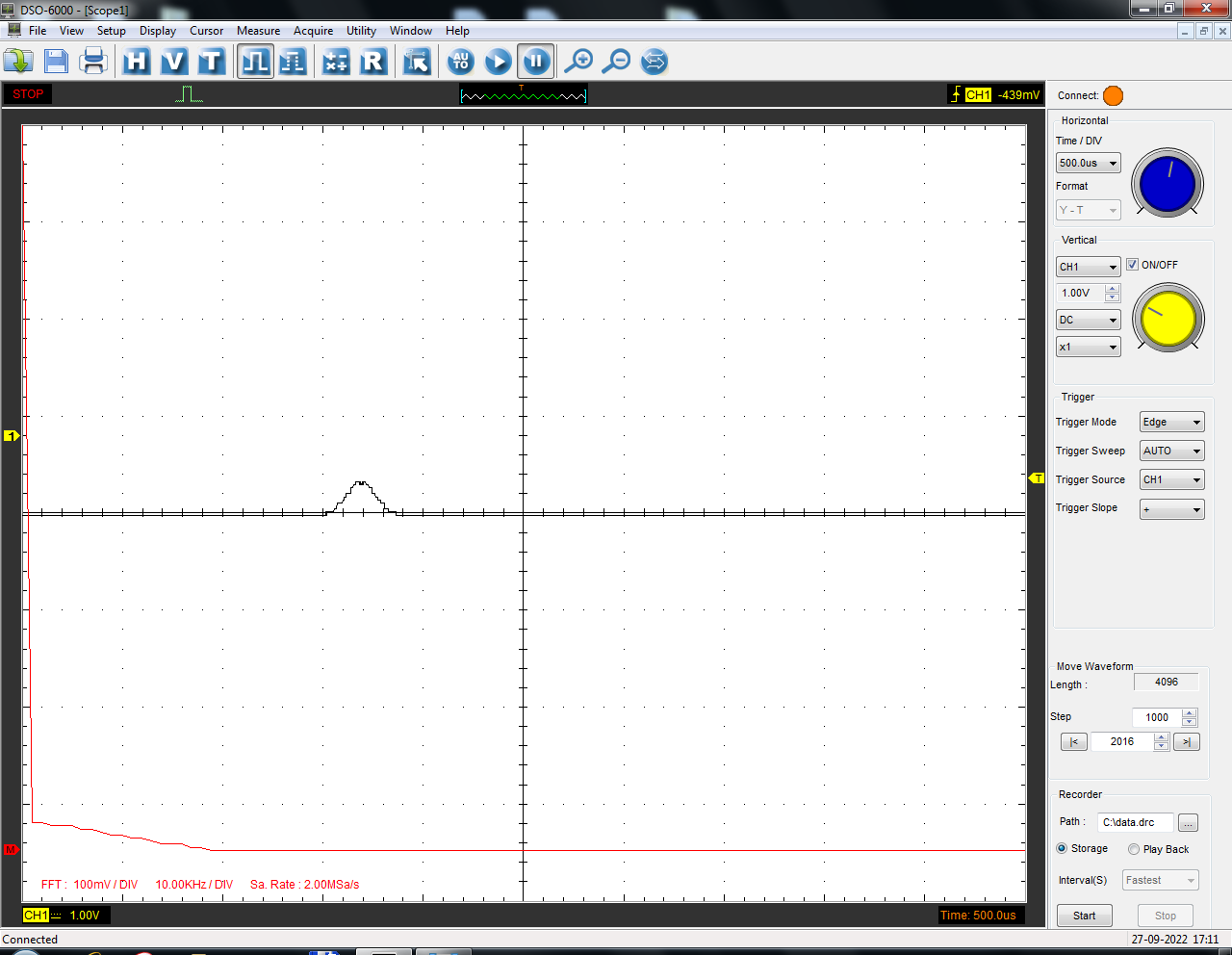 44 кГц: 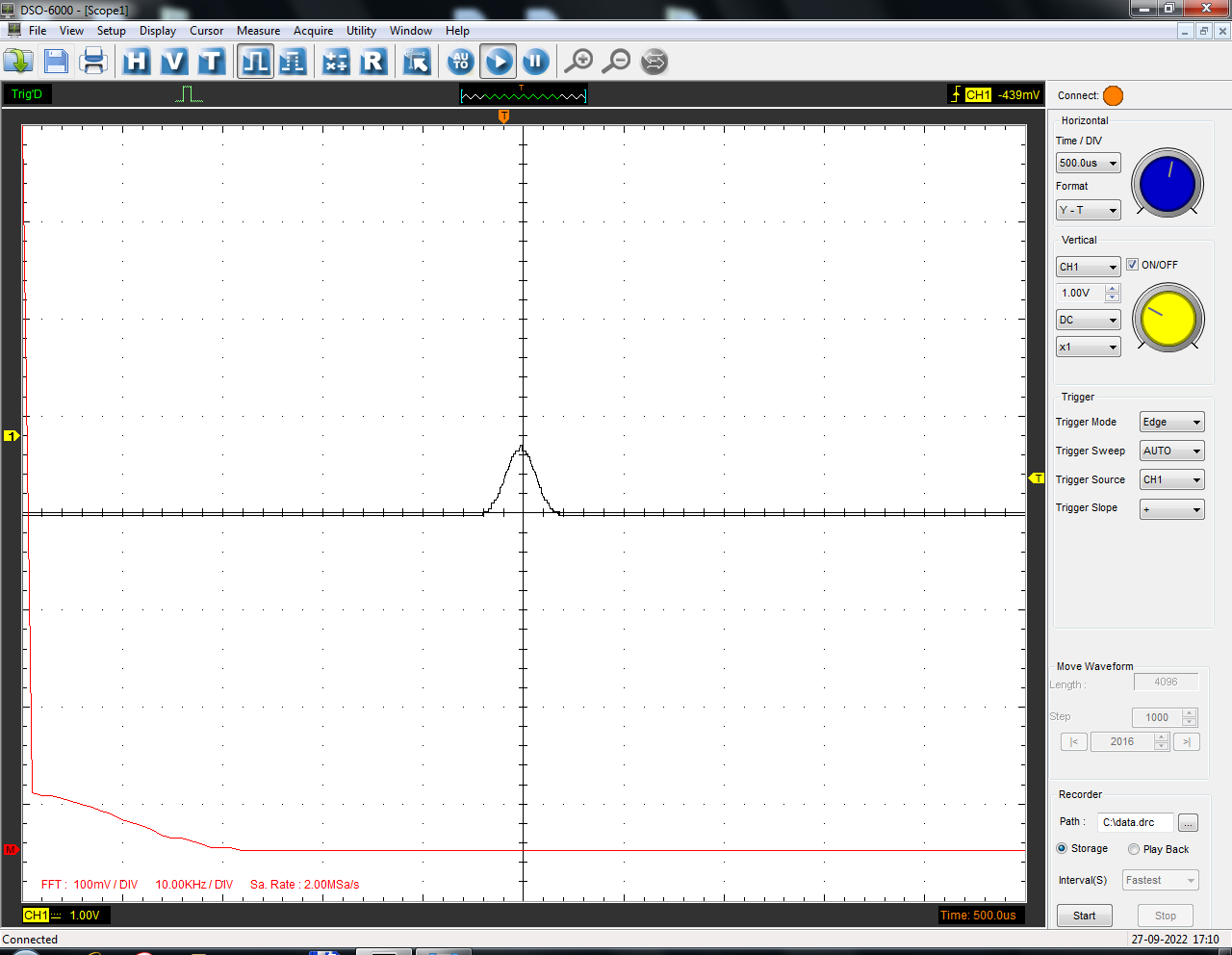 PF: 22 кГц: 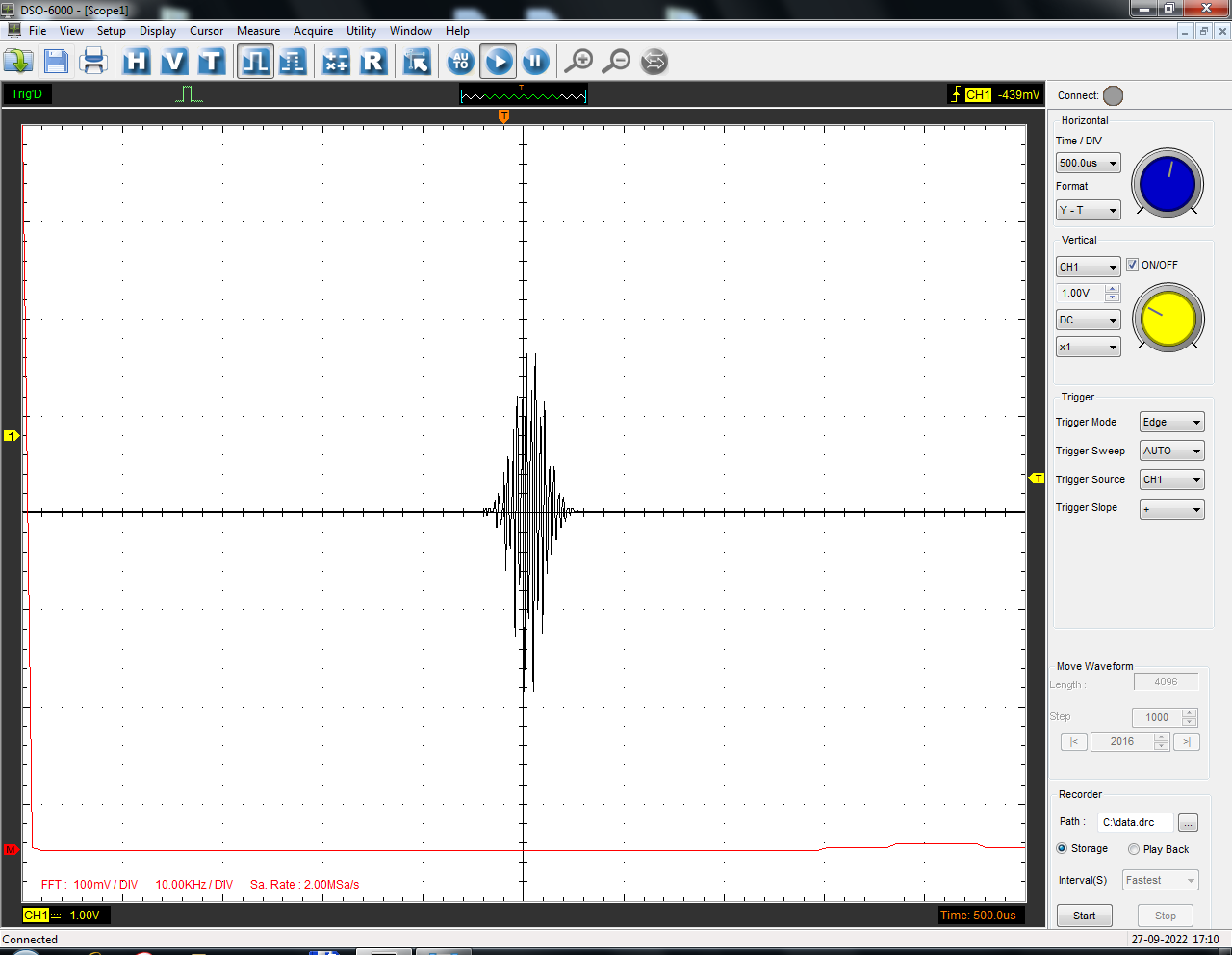 44 кГц: 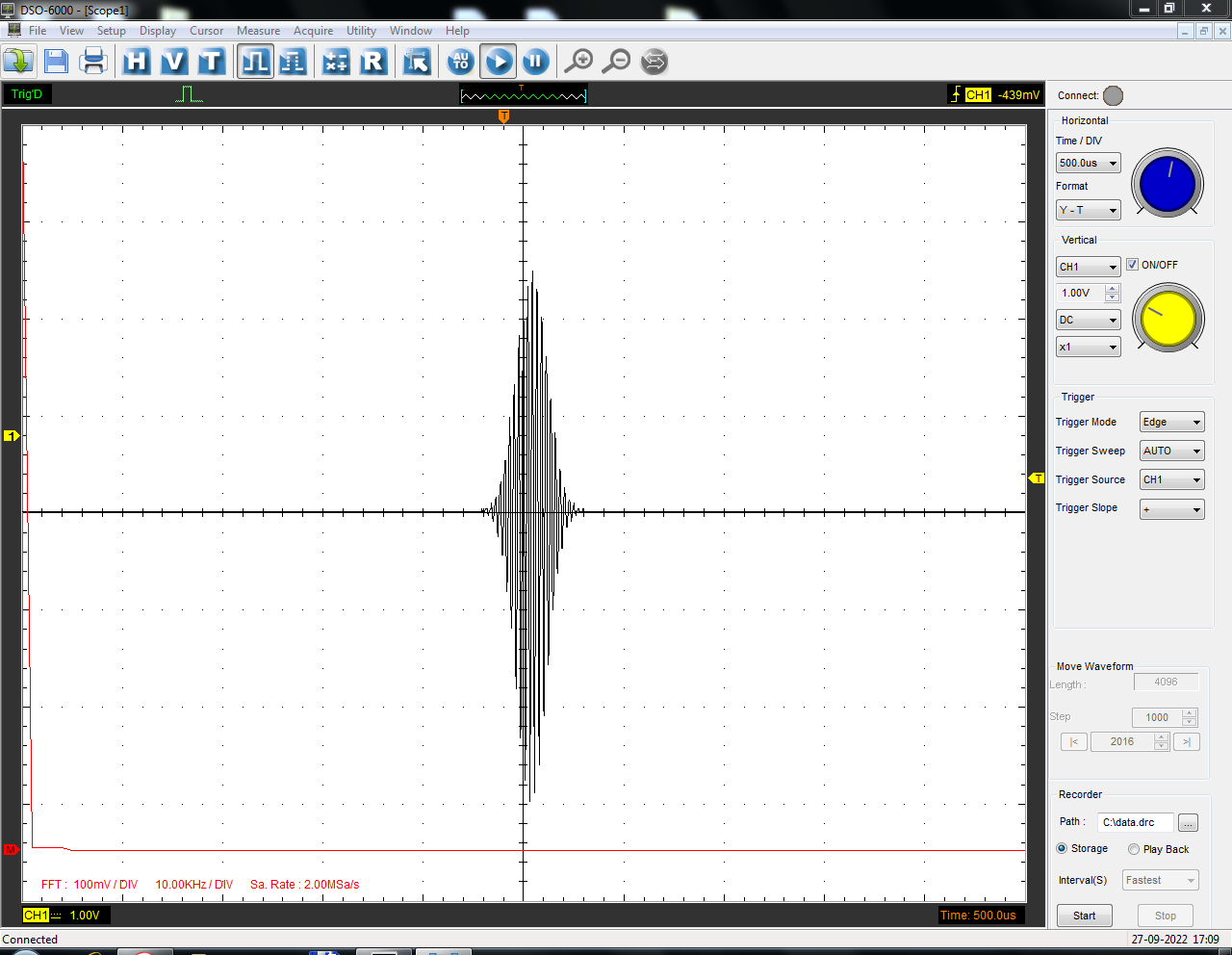 RC: 22 кГц: 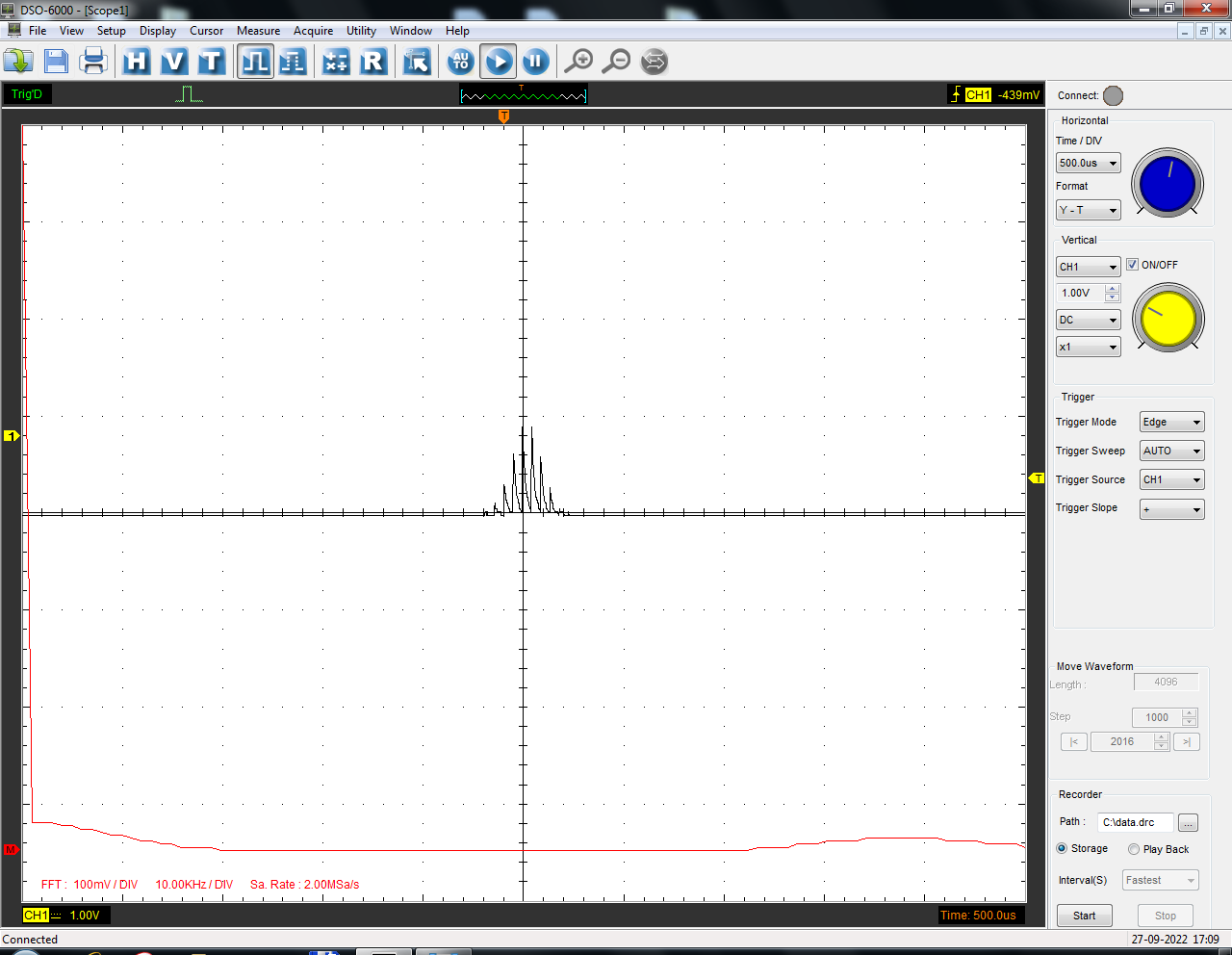 44 кГц: 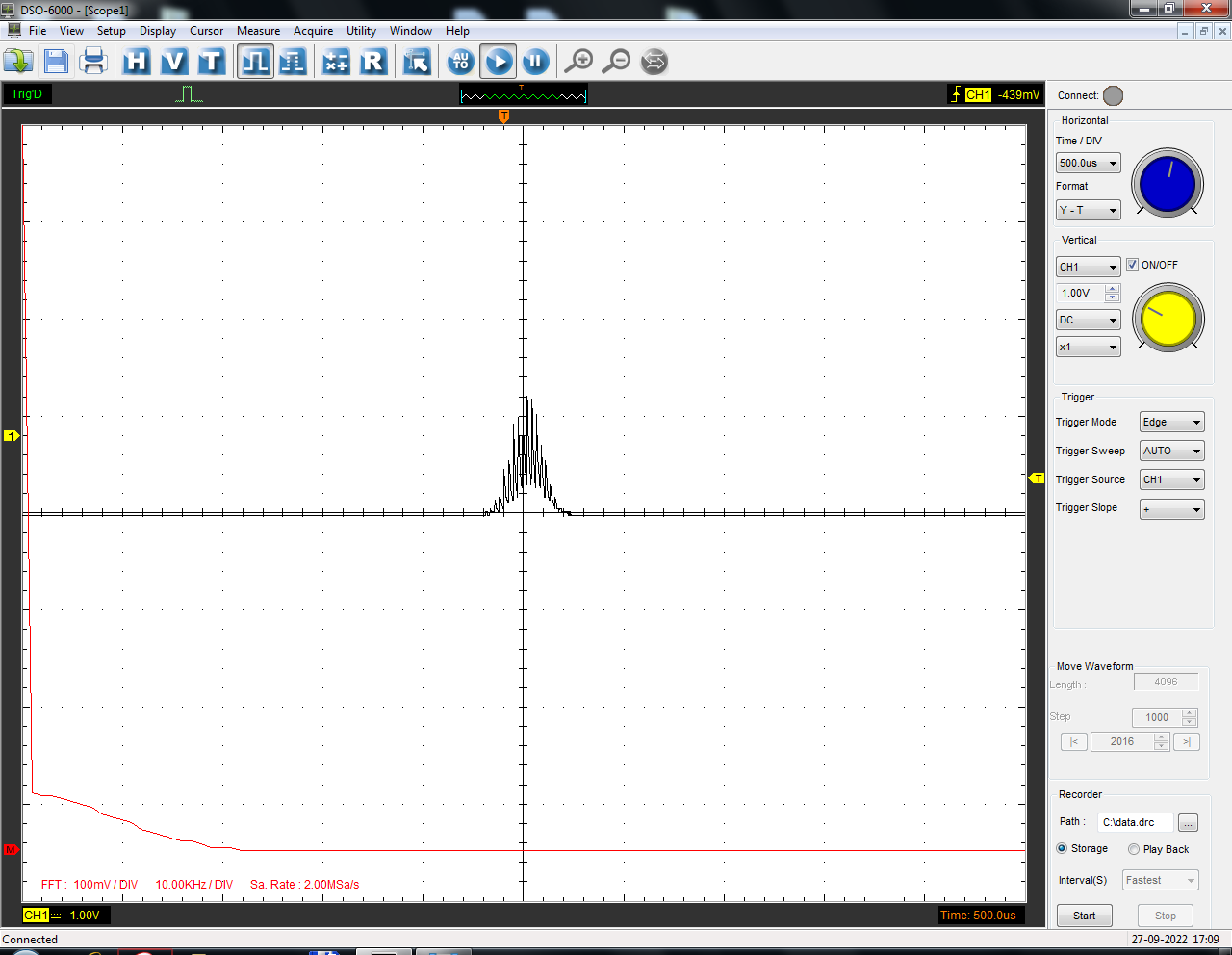 4-ый сигнал: FN: 22 кГц: 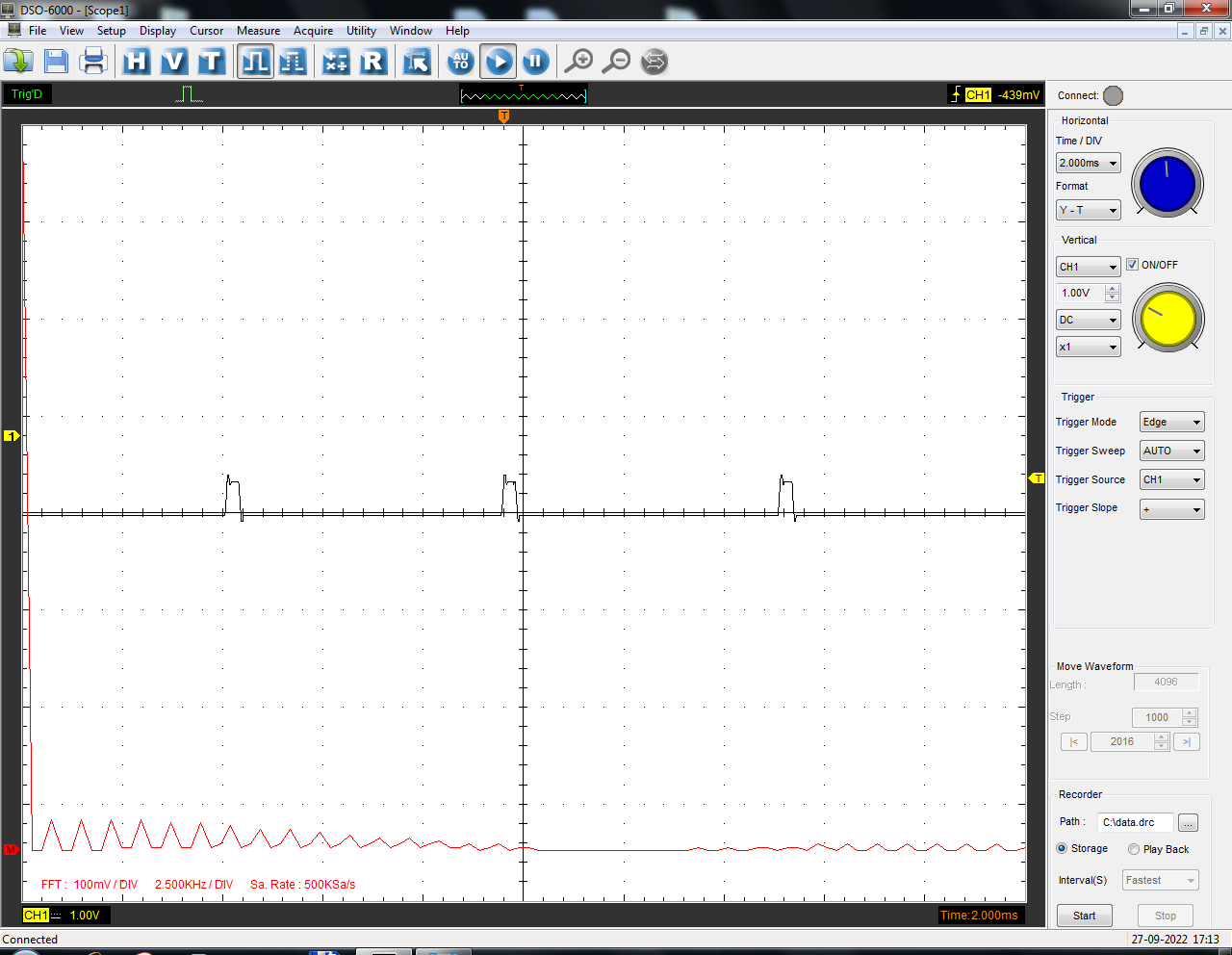 44 кГц: 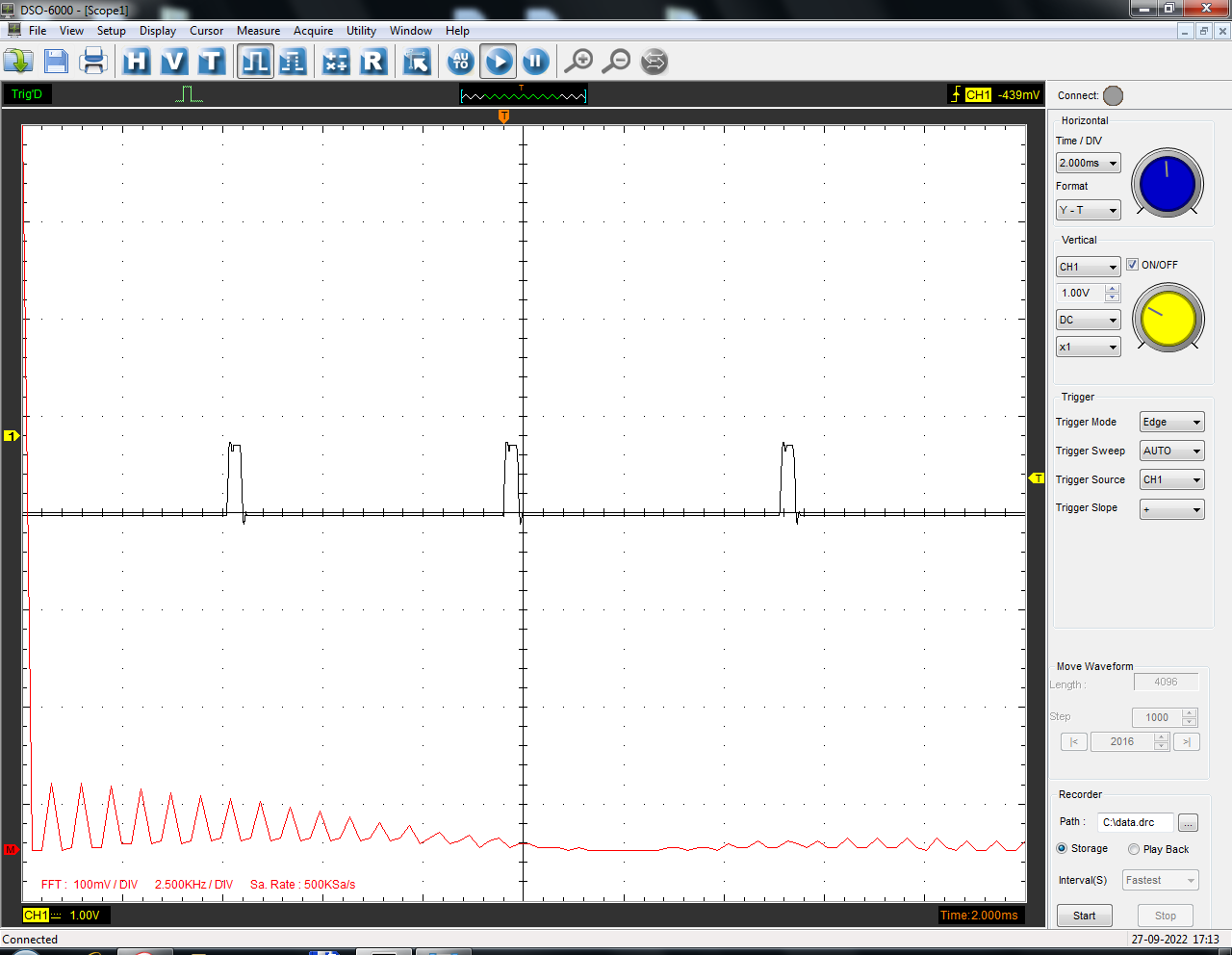 PF: 22 кГц: 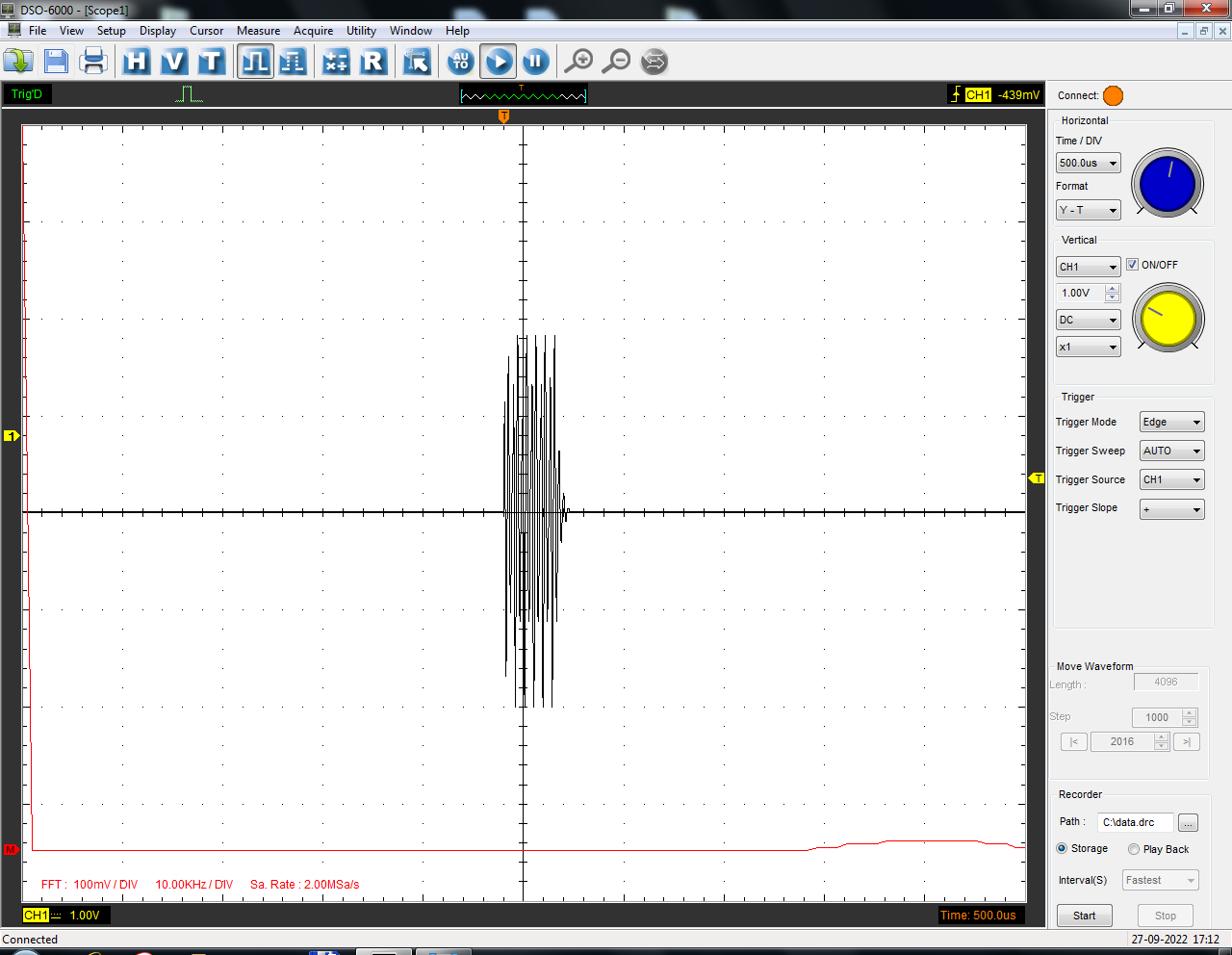 44 кГц: 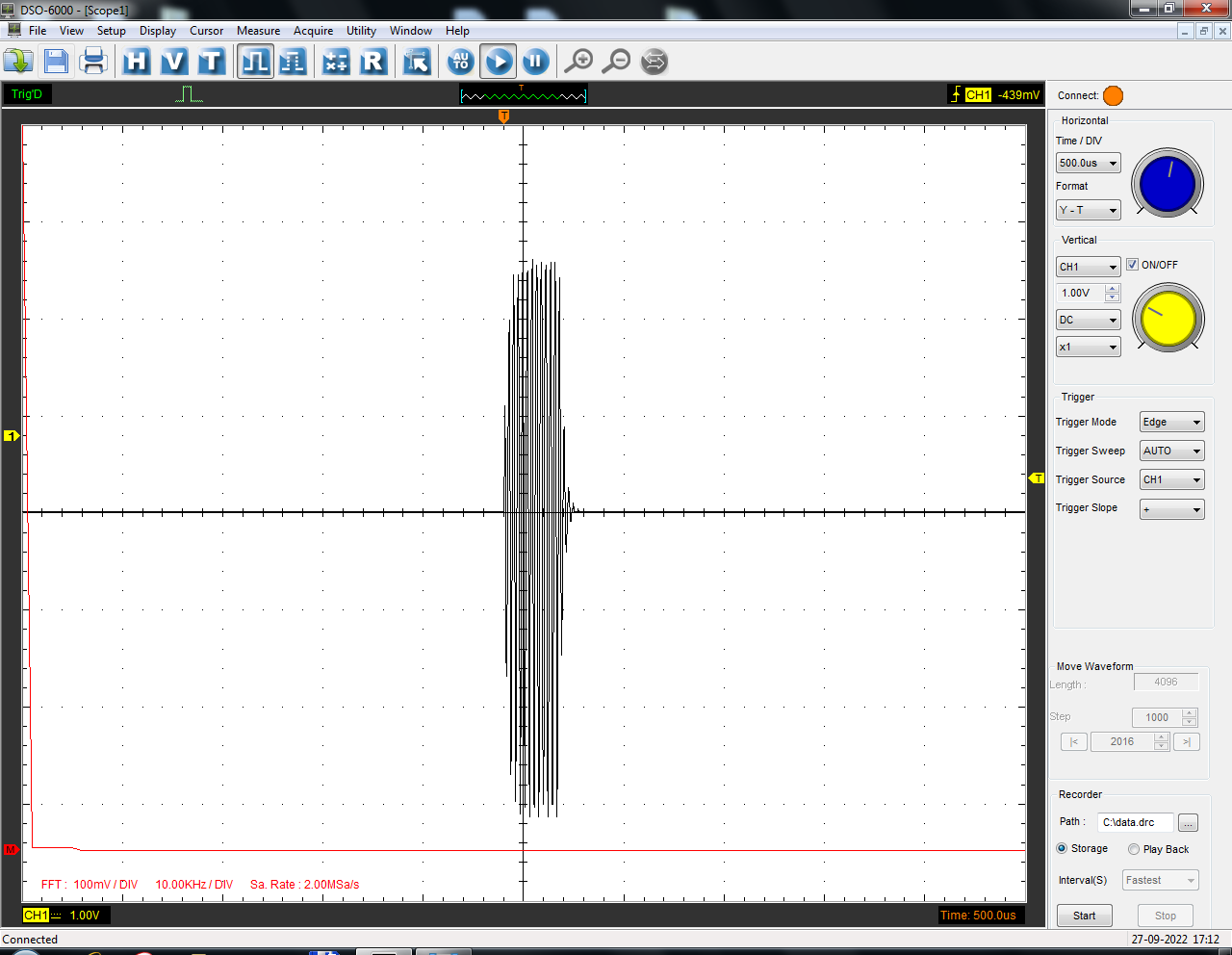 RC: 22 кГц: 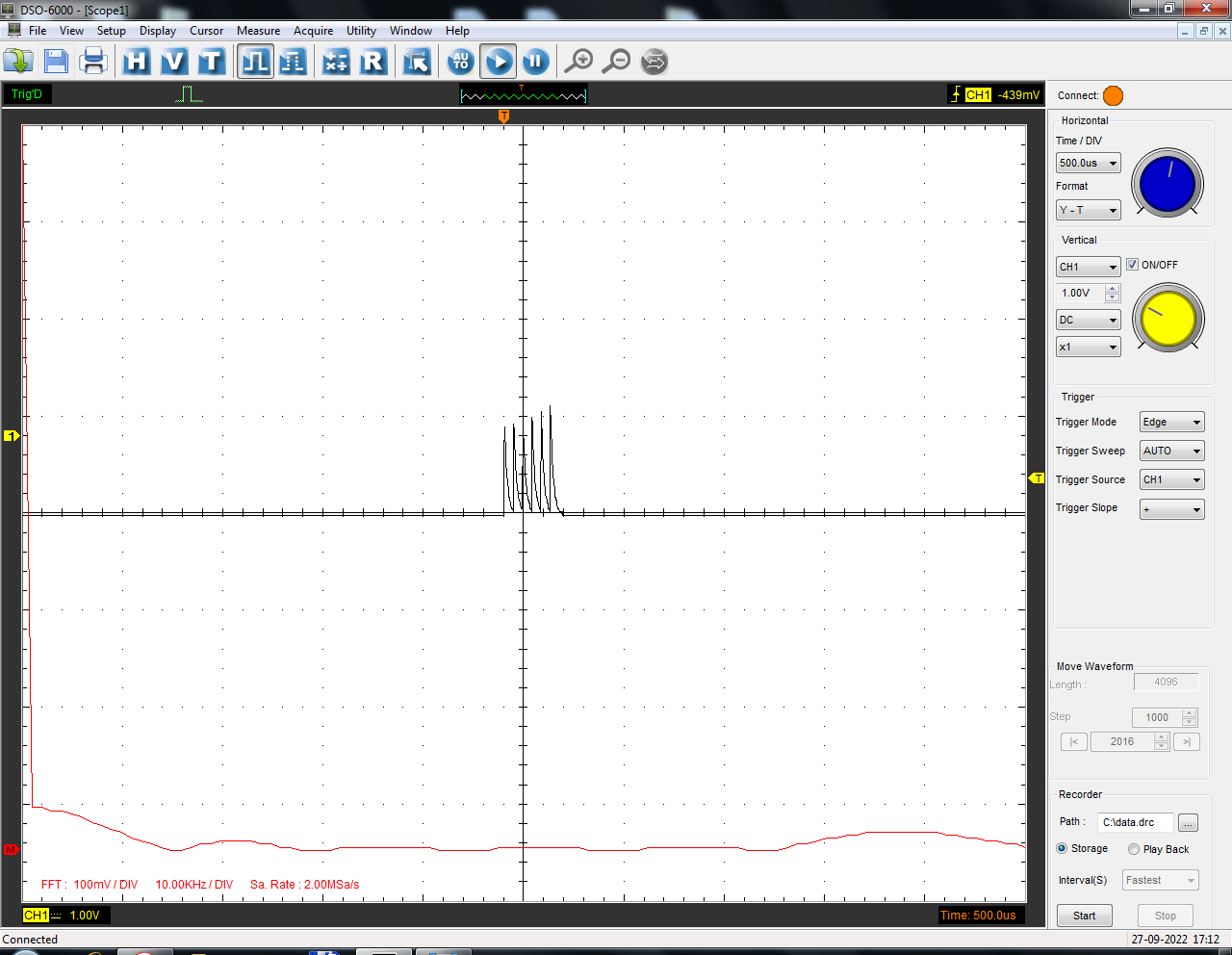 44 кГц: 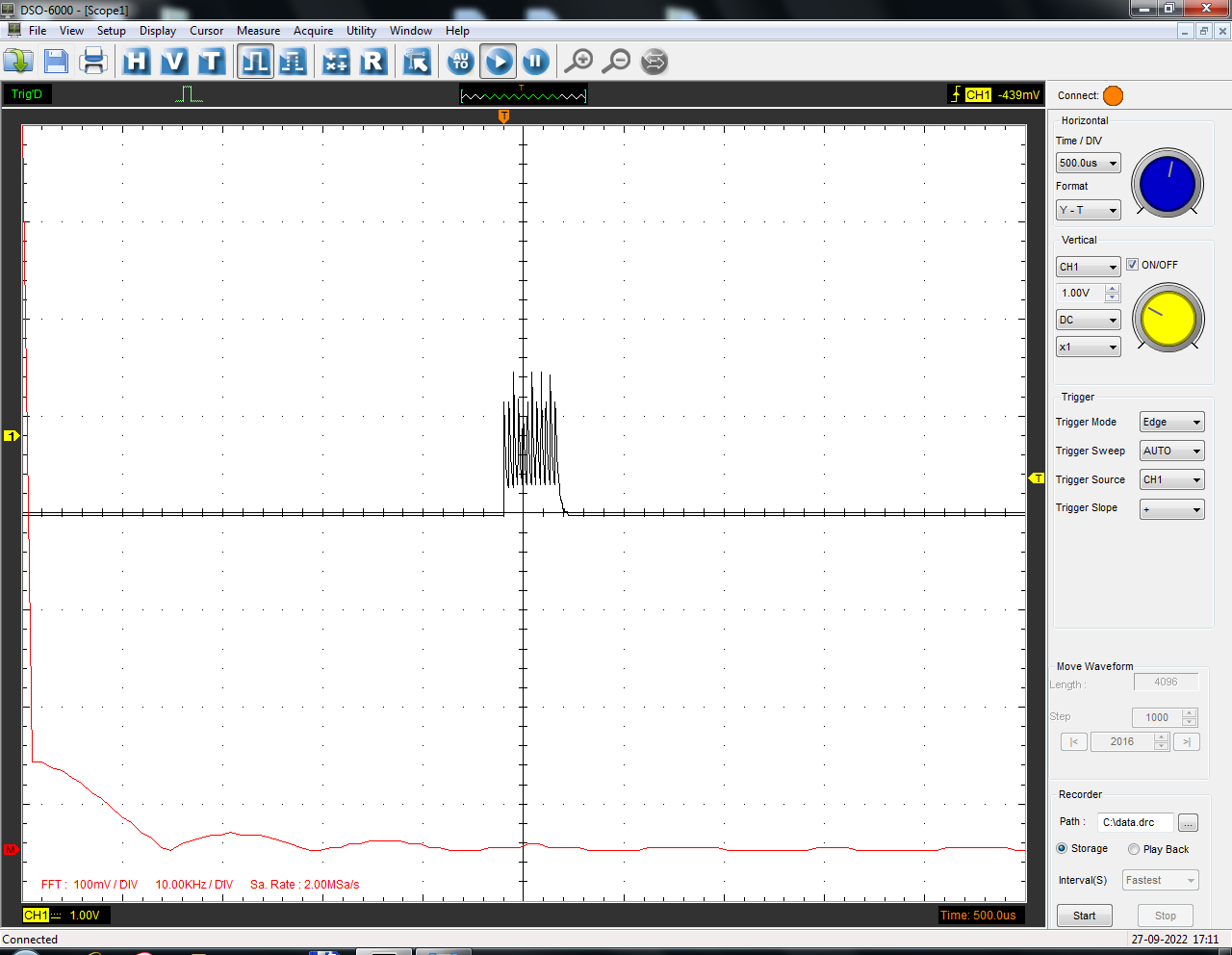 Исследовать процесс восстановления гармонического колебания с частотой, равной fд / 2, при изменении начальной фазы последовательности дискретизирующих импульсов. Зарисовать осциллограммы для трех различных вариантов указанной начальной фазы Максимум: 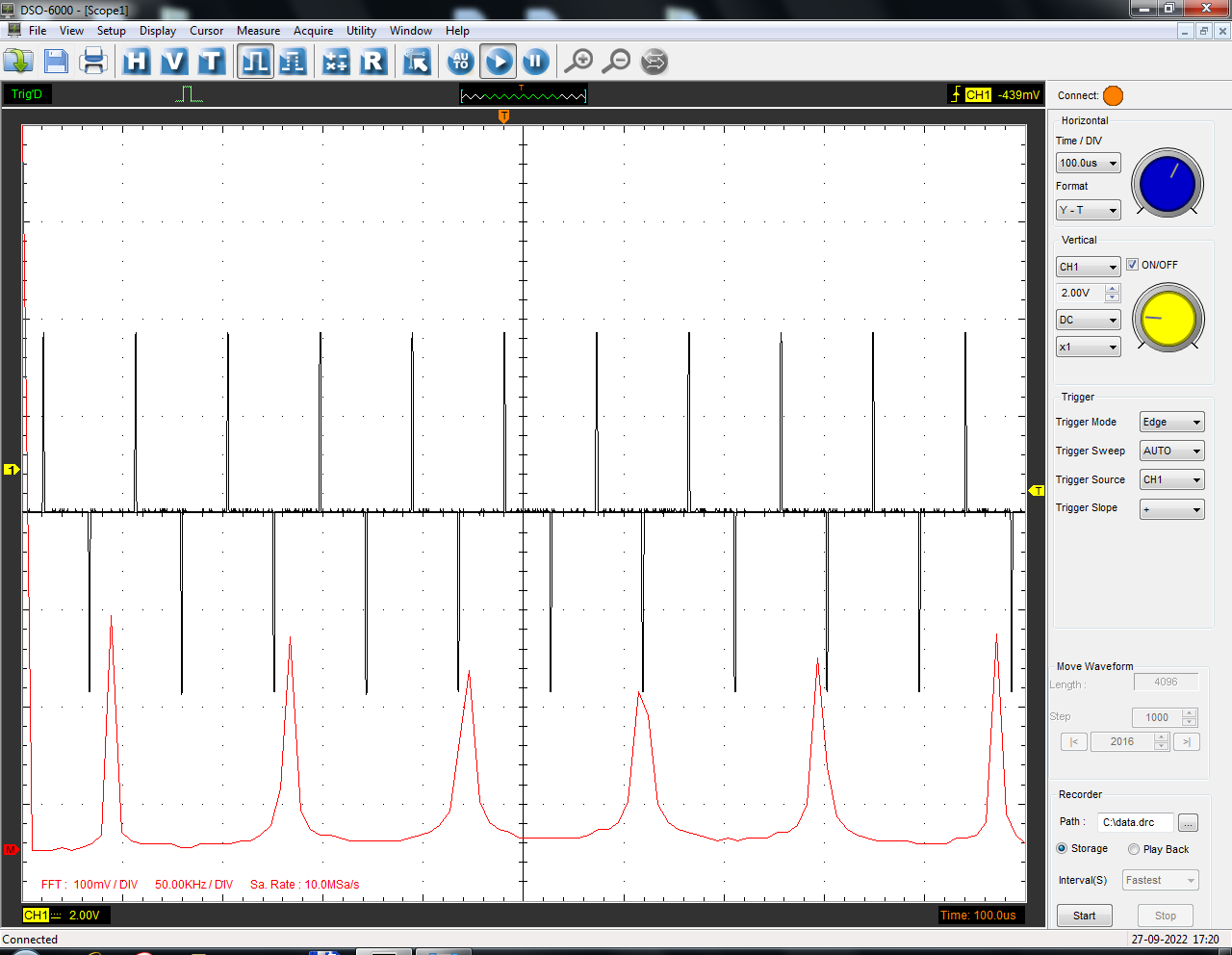 Среднее значение: 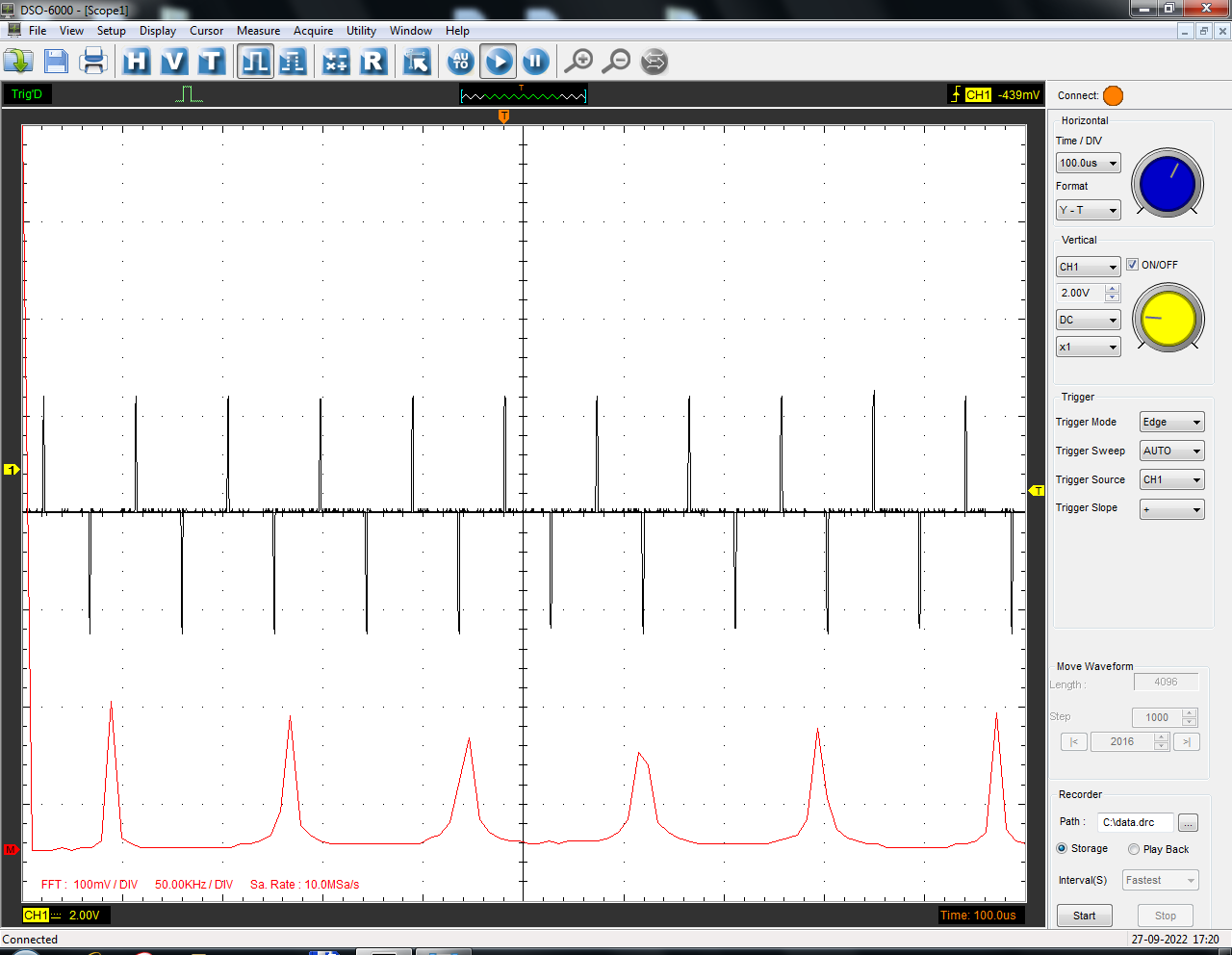 Минимум: 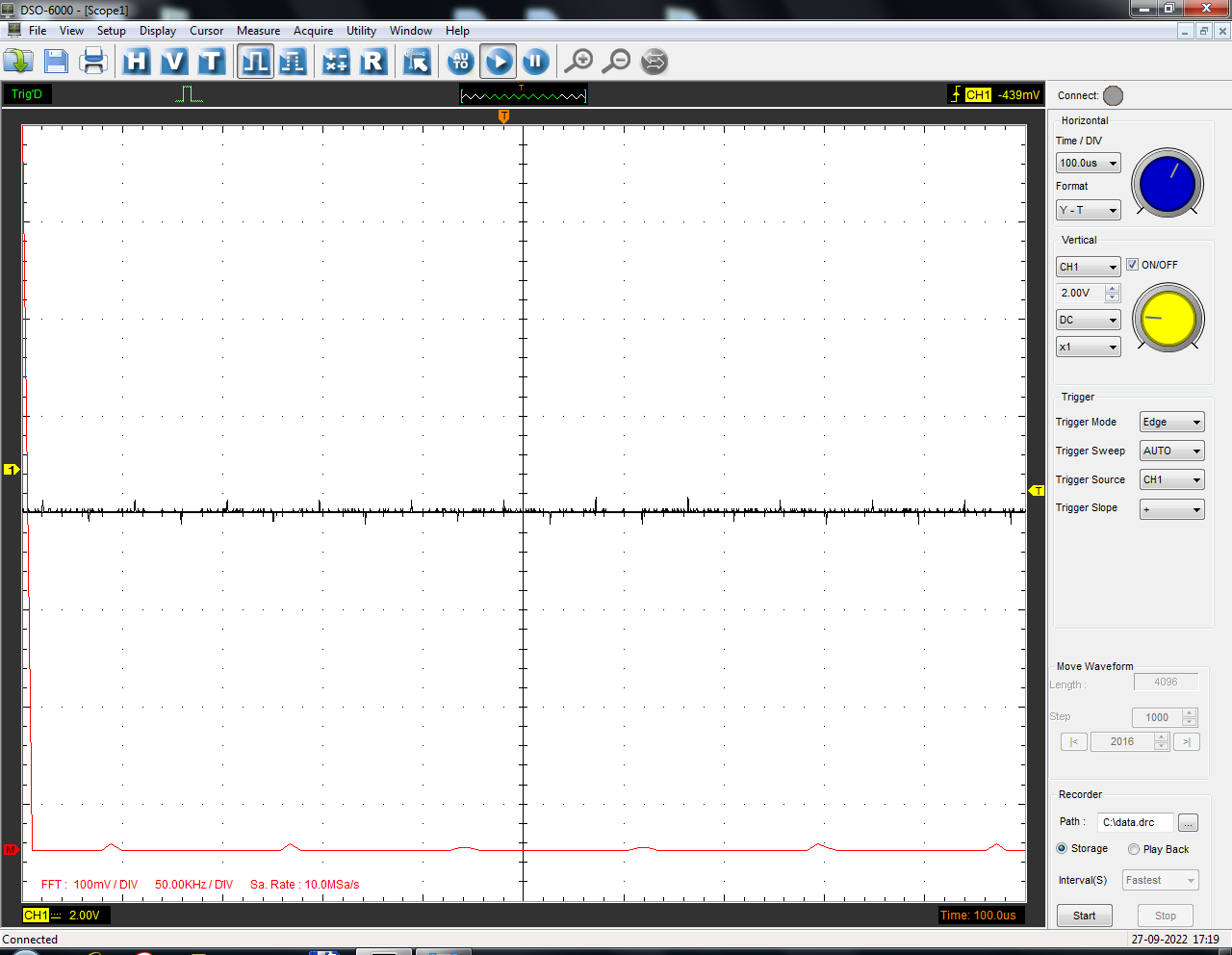 Вывод: Дискретизация сигнала применяется для замены непрерывного и передачи его в уже этом виде в дискретные устройства. Дискретный сигнал – совокупность ортогональных функций на интервале Т. Дискретизация сигнала выполняется разложением в ряд Фурье с соблюдением теоремы Котельникова. Так как в природе нет сигналов, ограниченных по времени и имеющих спектр используют 80-95% этого сигнала, то есть те, где сосредоточена почти вся информация сигнала. Для восстановления сигналоа используют идеальный фильтр нижних частот (ИФНЧ) с частотой среза 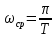 . Если на вход ИФНЧ подать периодическую последовательность δ-импульсов с периодом Т, то на его выходе возникнет периодическая последовательность откликов вида . Если на вход ИФНЧ подать периодическую последовательность δ-импульсов с периодом Т, то на его выходе возникнет периодическая последовательность откликов вида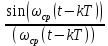 . .В реальности на ФНЧ подается дискретизированный сигнал s(kT), представляющий собой последовательность коротких импульсов, длительность которых много меньше интервала дискретизации T, а их амплитуды равны отсчетам s(kT). Таким образом, на выходе ФНЧ формируется сумма, т. е. восстановленный сигнал s(t). Если частота дискретизации 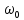 выбрана меньше, чем выбрана меньше, чем 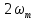 , то получим частичное наложение (перекрытие) участков размноженного исходного спектра. В результате такого наложения спектр исказится и после выделения ИФНЧ участка спектра [ , то получим частичное наложение (перекрытие) участков размноженного исходного спектра. В результате такого наложения спектр исказится и после выделения ИФНЧ участка спектра [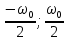 ] выходной сигнал будет несколько отличаться от исходного. Если же частота дискретизации ] выходной сигнал будет несколько отличаться от исходного. Если же частота дискретизации 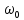 выбрана больше, чем выбрана больше, чем 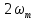 , наложения копий спектра не произойдет, сигнал на выходе ИФНЧ восстановится без искажения. , наложения копий спектра не произойдет, сигнал на выходе ИФНЧ восстановится без искажения.Используя полосовой фильтр с идеальной частотной характеристикой, можно выделить один из участков спектра со средней частотой 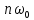 , где n = 1, 2, …, и сформировать радиоимпульс с частотой заполнения , где n = 1, 2, …, и сформировать радиоимпульс с частотой заполнения 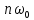 и огибающей, совпадающей с исходным сигналом. и огибающей, совпадающей с исходным сигналом. |
