работа. Синус, косинус, тангенс и котангенс
 Скачать 34.74 Kb. Скачать 34.74 Kb.
|
|
Синус, косинус, тангенс и котангенс. Для начала нарисуем в тетрадке самый обычный прямоугольный треугольник. Стороны его обозначим как a, b и c, а один из острых углов обозначим буквой α. Это греческая буква "альфа". На всякий случай, напомню, что стороны, образующие прямой угол, называются катетами (a и b – катеты), а третья сторона, лежащая напротив прямого угла, называется гипотенузой (c – гипотенуза). Кстати, страшное слово "тригонометрия" с древнегреческого языка на русский так и переводится – измерение треугольников. Кстати сказать, прямоугольный треугольник со сторонами 3, 4, 5 – весьма интересная фигура! Он известен ещё с античных времён и называется египетским треугольником. Ибо активно применялся для построения прямых углов египетскими землемерами и архитекторами. В том числе и при построении пирамид, между прочим.) А вообще, целые числа a, b, c, которые могут быть длинами сторон прямоугольного треугольника, т.е. для которых выполняется теорема Пифагора: Квадрат гипотенузы равен сумме квадратов катетов. a2 + b2 = c2 в математике так и называются – пифагоровыми тройками. Тройка (3; 4; 5) – самая известная. Ещё распространена тройка чисел (5; 12; 13). Или (8; 15; 17). Таких троек известно очень и очень много. Теперь сделаем следующее. Поделим длину катета a на длину катета b. Или, как принято говорить в математике, возьмём отношение a к b. Получим: a/b = 3/4 А теперь увеличим треугольник, продлив стороны b и c, но не как попало, а так, чтобы наш треугольник остался прямоугольным. Угол α, как видно, остался прежним. Старые стороны a, b и с превратились в новые стороны x, y, z. Их длины, естественно, изменились, увеличившись вдвое: Стало: x/y = 6/8 = 3/4. И для других соответствующих сторон их отношения также не изменятся. Можно что угодно делать с треугольником – увеличивать, уменьшать, сохраняя при этом угол α, а отношения соответствующих сторон всё равно останутся прежними. Соотношения сторон в прямоугольном треугольнике никак не зависят от длин этих самых сторон при одном и том же угле α. Синус угла α - это отношение противолежащего катета к гипотенузе: sin α = a/c Косинус угла α - это отношение прилежащего катета к гипотенузе: cos α = b/c Тангенс угла α - это отношение противолежащего катета к прилежащему: tg α = a/b Котангенс угла α - это отношение прилежащего катета к противолежащему: ctg α = b/a Вся эта великолепная четвёрка (синус, косинус, тангенс и котангенс) называется тригонометрическими функциями. Например: синус угла – это отношения дальнего от угла (т.е. противолежащего) катета к гипотенузе, а косинус – отношение ближнего (т.е. прилежащего) катета к гипотенузе. Тангенс – отношение дальнего от угла катета к ближнему. А котангенс – наоборот. 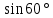 = = 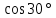 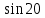 ° = ° = 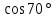 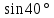 = = 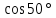 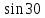 = = 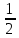 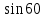 = = 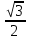 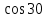 = = 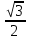 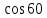 = = 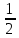 Пифагор родился на острове Самос в IV в до н.э. Организовал там Пифагорейскую школу. Пифагора считают отцом нумерации, описывающей с помощью чисел весь мир, раскрывающей прошлое и будущее, предсказывающей судьбы людей. Они верили, что в числовых закономерностях спрятана тайна мира. Четные - счастливые, нечетные- несчастливые. Числа - пифагоровы тройки. (3;4;5), (6;8;10), (5:12;13), (12;16;20), (10;24;26), (20;21;29). Пифагор доказал теорему, которая носит его имя. Сейчас существует более ста доказательств этой теоремы. Задание Выучите наизусть теорему Пифагора, определения синуса, косинуса, тангенса и котангенса. По таблице изучите и запишите подробно решение задач, постарайтесь у всех треугольников найти синус, косинус и тангенс острых углов. 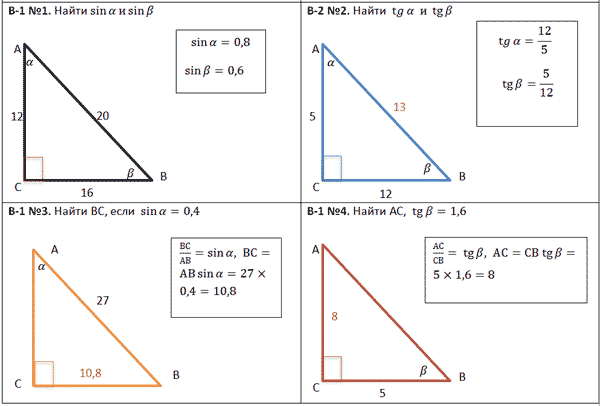 Повторение пройденного: Площадь треугольника равна половине произведения его основания на высоту. Площадь прямоугольника равна произведению длины на ширину. Площадь прямоугольного треугольника равна половине произведения катетов. Катет, лежащий против угла в 30 ° равен половине гипотенузы. Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы. Средняя линия треугольника параллельна основанию и равна его половине. |
